Нормальное уравнение плоскости
Три точки в пространстве 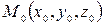 ,
, 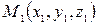 и
и 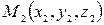 , не лежащие на одной прямой, определяют единственную плоскость. Очевидно, что точка
, не лежащие на одной прямой, определяют единственную плоскость. Очевидно, что точка 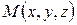 лежит в этой плоскости тогда и только тогда, когда векторы
лежит в этой плоскости тогда и только тогда, когда векторы
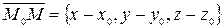 ,
,
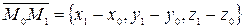 ,
,
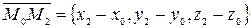
компланарны. В соответствии с критерием компланарности это равносильно тому, что смешанное произведение указанных векторов равно нулю:
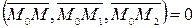
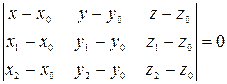 .
.
Последнее равенство и является уравнением плоскости, проходящей через данные три точки. Если расписать этот определитель (например, по элементам первой строки), то получим общее уравнение плоскости.
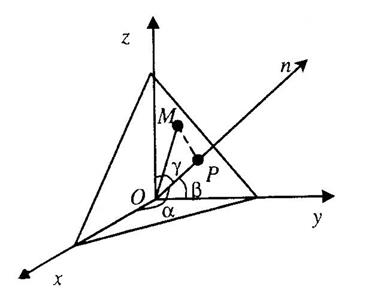 Пусть плоскость определяется заданием вектора нормали
Пусть плоскость определяется заданием вектора нормали 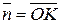 , опущенного на плоскость из начала координат и длиной
, опущенного на плоскость из начала координат и длиной 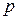 этого вектора. Пусть также
этого вектора. Пусть также 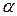 ,
, 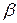 ,
, 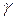 - углы, образованные вектором
- углы, образованные вектором 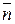 с координатными осями
с координатными осями 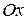 ,
, 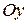 и
и 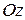 . Тогда единичный, сонаправленный с вектором
. Тогда единичный, сонаправленный с вектором 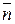 , вектор
, вектор 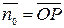 имеет координаты:
имеет координаты: 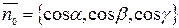 . Точка
. Точка 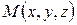 лежит в указанной плоскости тогда и только тогда, когда справедливо равенство
лежит в указанной плоскости тогда и только тогда, когда справедливо равенство
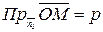 .
.
Так как
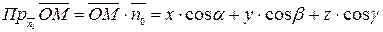 ,
,
то критерий принадлежности точки  рассматриваемой плоскости может быть описан равенством:
рассматриваемой плоскости может быть описан равенством:
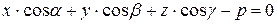 .
.
Полученное равенство является уравнением данной плоскости, называемым ее нормальным уравнением.
Отклонением 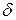 точки
точки  от данной плоскости называется расстояние
от данной плоскости называется расстояние 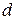 от этой точки до плоскости, взятое со знаком плюс, если точка
от этой точки до плоскости, взятое со знаком плюс, если точка  и начало координат лежат по разные стороны от рассматриваемой плоскости, и взятое со знаком минус, если точка
и начало координат лежат по разные стороны от рассматриваемой плоскости, и взятое со знаком минус, если точка  и начало координат лежат по одну сторону от рассматриваемой плоскости.
и начало координат лежат по одну сторону от рассматриваемой плоскости.
Рассмотрим произвольную точку 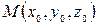 пространства. Спроектируем эту точку на вектор
пространства. Спроектируем эту точку на вектор 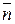 . Пусть
. Пусть 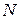 - полученная проекция. Отклонение точки
- полученная проекция. Отклонение точки 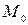 от данной плоскости равно
от данной плоскости равно 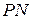 . Очевидно, что
. Очевидно, что
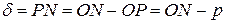 .
.
При этом
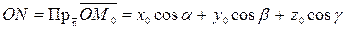 .
.
Таким образом,
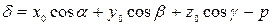 .
.
Другими словами, для нахождения отклонения точки от плоскости следует в левую часть нормального уравнения плоскости подставить вместо 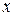 ,
, 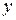 и
и 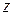 координаты этой точки. Очевидно, что расстояние от точки
координаты этой точки. Очевидно, что расстояние от точки 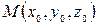 до плоскости
до плоскости 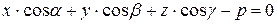 определяется равенством:
определяется равенством:
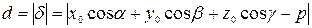
Отметим, что общее уравнение плоскости
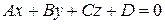
Можно привести к нормальному виду так, как это делалось для уравнения прямой на плоскости. Для этого нужно подобрать число 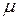 такое, что
такое, что
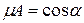 ,
,
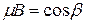 ,
,
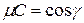 ,
,
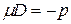 .
.
Возводя в квадрат первые три равенства, складывая их и учитывая, что сумма квадратов направляющих косинусов равна единице, получим:
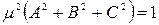 ,
,
Откуда
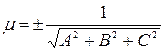 .
.
Из равенства 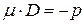 следует, что знак
следует, что знак 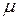 должен выбираться противоположным знаку свободного коэффициента
должен выбираться противоположным знаку свободного коэффициента 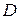 . Число
. Число 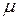 , определяемое таким образом, называется нормирующим множителем. Если умножить обе части общего уравнения на нормирующий множитель, то получим нормальное уравнение. В соответствии с этими рассуждениями заключаем, что расстояние от точки
, определяемое таким образом, называется нормирующим множителем. Если умножить обе части общего уравнения на нормирующий множитель, то получим нормальное уравнение. В соответствии с этими рассуждениями заключаем, что расстояние от точки 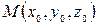 до плоскости
до плоскости 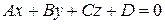 определяется формулой:
определяется формулой:
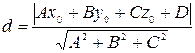 .
.
Пример.Найти нормальное уравнение плоскости, проходящей через точки 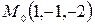 ,
, 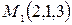 ,
, 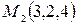 .
.
∆ Воспользуемся формулой для нахождения уравнения плоскости, проходящей через заданные три точки 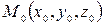 ,
, 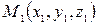 и
и 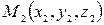 :
:
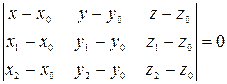 .
.
В результате получим:
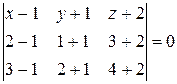
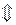
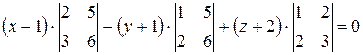
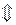
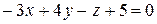
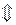
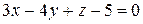 .
.
Полученное уравнение является общим уравнением плоскости. Приведем его к нормальному виду. Для этого найдем нормирующий множитель:
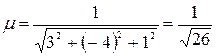 .
.
Умножим обе части общего уравнения плоскости на найденный нормирующий множитель:
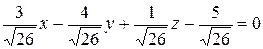 .
.
Это и есть нормальное уравнение данной плоскости. ▲
