Сечения цилиндра плоскостью
Начальные понятия
| Окружность | Геометрическая фигура, состоящая из всех точек плоскости, находящихся на заданном расстоянии от данной точки этой плоскости. Данная точка называется центром окружности. |
| Радиус окружности | Отрезок, соединяющий центр окружности с какой-либо точкой этой окружности |
| Хорда окружности | Отрезок, соединяющий две точки окружности |
| Диаметр окружности | Хорда, проходящая через центр окружности |
| Дуга окружности | Каждая из частей окружности, на которые делят окружность любые две её точки |
| Касательная к окружности | Прямая, имеющая с окружностью только одну общую точку. Эта точка называется точкой касания. |
| Круг | Геометрическая фигура, состоящая из окружности и части плоскости, ограниченной этой окружностью |
| Круговой сектор | Часть круга, ограниченная двумя радиусами и дугой окружности |
| Круговой сегмент | Часть круга, ограниченная дугой окружности и хордой |
| Геометрическое тело | Ограниченная фигура в пространстве, обладающая следующими свойствами: 1) у неё есть внутренние точки, и любые две из них можно соединить ломаной, каждая точка которой является внутренней точкой фигуры; 2) фигура содержит свою границу и её граница совпадает с границей её внутренности. Граница тела называется его поверхностью. |
2.1.Понятие тела вращения. Виды поверхностей и тел вращения
1) 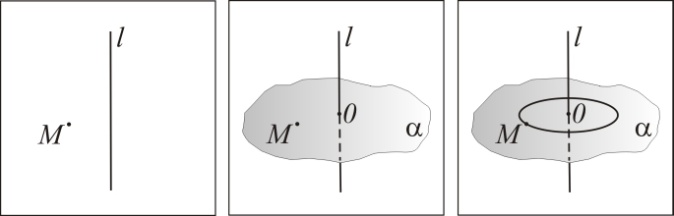 Пусть дана прямая l и точка MÏl. Через точку M проведём плоскость a^l, aÇl=O. Рассмотрим окружность с центром в точке O и радиусом OM. О такой окружности говорят, что она получена в результате вращения точки M вокруг оси l.
Пусть дана прямая l и точка MÏl. Через точку M проведём плоскость a^l, aÇl=O. Рассмотрим окружность с центром в точке O и радиусом OM. О такой окружности говорят, что она получена в результате вращения точки M вокруг оси l.
2)  Рассмотрим фигуру F, принадлежащую плоскости, содержащей прямую l. Каждой точке фигуры F поставим в соответствие окружность, полученную при вращении данной точки вокруг прямой l. Объединение всех таких окружностей и точек фигуры F, принадлежащих прямой l, называется фигурой вращения, полученной в результате вращения фигуры F вокруг прямой l, которая называется осью вращения.
Рассмотрим фигуру F, принадлежащую плоскости, содержащей прямую l. Каждой точке фигуры F поставим в соответствие окружность, полученную при вращении данной точки вокруг прямой l. Объединение всех таких окружностей и точек фигуры F, принадлежащих прямой l, называется фигурой вращения, полученной в результате вращения фигуры F вокруг прямой l, которая называется осью вращения.
Если при этом фигура является ограниченной и обладает всеми свойствами геометрического тела, то её называют телом вращения.
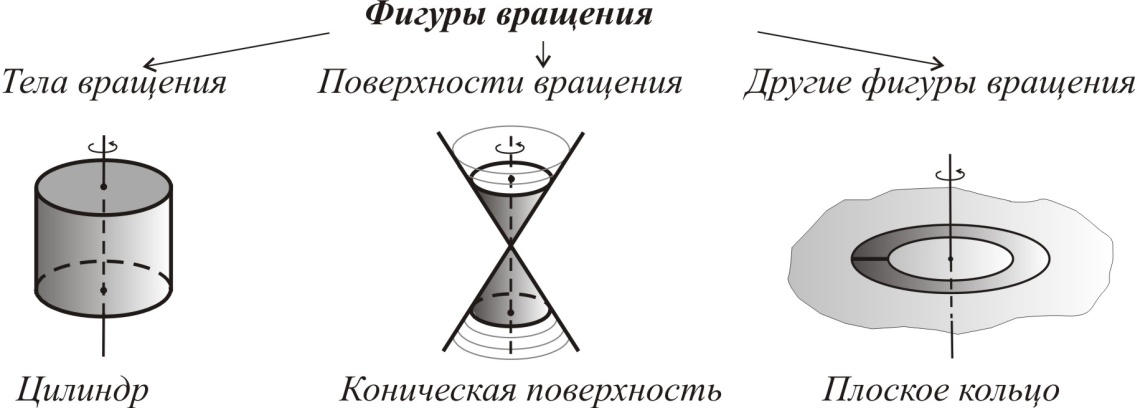
Виды поверхностей вращения
1) Цилиндрическая поверхность – результат вращения прямой, параллельной оси вращения.
2) Коническая поверхность – результат вращения прямой, не параллельной и не перпендикулярной оси вращения.
3) Сфера – результат вращения полуокружности вокруг диаметра.
Виды тел вращения
1) Цилиндр – результат вращения прямоугольника вокруг одной из его сторон.
2) Конус – результат вращения прямоугольного треугольника вокруг одного из катетов.
3) Шар – результат вращения полукруга вокруг диаметра.
2.2. Цилиндр. Боковая поверхность цилиндра. Объём цилиндра. Сечения цилиндра. Сечения цилиндрической поверхности
Можно выделить три подхода к определению понятия цилиндра:
Через понятие тела вращения Тело вращения –фигура вращения, полученная в результате вращения геометрической фигуры вокруг прямой, лежащей в плоскости этой фигуры, обладающая всеми свойствами геометрического тела. 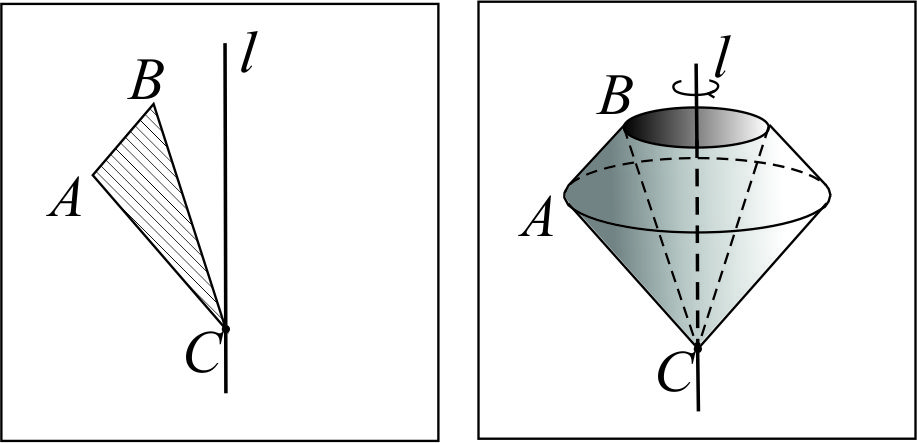 | Через понятие обобщённого цилиндра 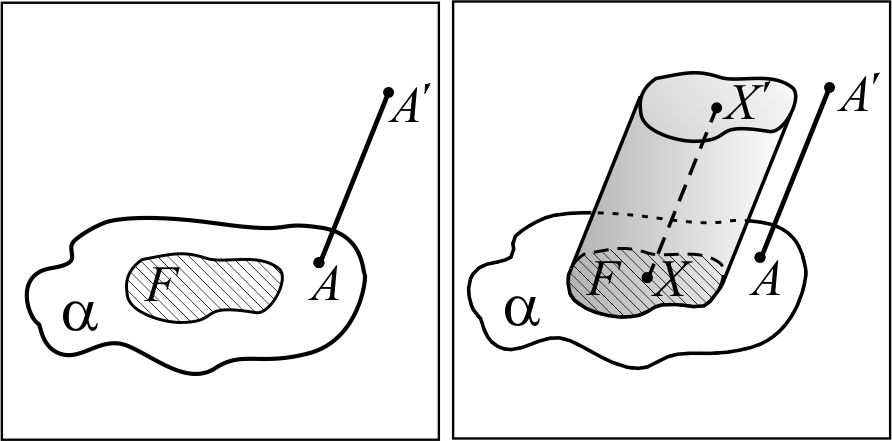 Рассмотрим фигуру F, лежащую в некоторой плоскости α и отрезок AA¢, не лежащий в этой плоскости, AÎα. Из каждой точки X фигуры F проведём отрезок XX¢ || AA¢. Фигура, образованная всеми отрезками XX¢, лежащими по одну сторону от плоскости α, называется обобщённым цилиндром. Если AA¢^α, то обобщённый цилиндр называют прямым. Фигуры F и F¢, которая состоит из концов отрезков XX¢, не принадлежащих фигуре F, называются основаниями обобщённого цилиндра. Если точка X отрезка XX¢ принадлежит границе фигуры F, то отрезок XX¢ называется образующей обобщённого цилиндра. Фигура, состоящая из всех образующих, называется боковой поверхностью обобщённого цилиндра. Полной поверхностьюобобщённого цилиндра называется фигура, состоящая из боковой поверхности и двух его оснований. Рассмотрим фигуру F, лежащую в некоторой плоскости α и отрезок AA¢, не лежащий в этой плоскости, AÎα. Из каждой точки X фигуры F проведём отрезок XX¢ || AA¢. Фигура, образованная всеми отрезками XX¢, лежащими по одну сторону от плоскости α, называется обобщённым цилиндром. Если AA¢^α, то обобщённый цилиндр называют прямым. Фигуры F и F¢, которая состоит из концов отрезков XX¢, не принадлежащих фигуре F, называются основаниями обобщённого цилиндра. Если точка X отрезка XX¢ принадлежит границе фигуры F, то отрезок XX¢ называется образующей обобщённого цилиндра. Фигура, состоящая из всех образующих, называется боковой поверхностью обобщённого цилиндра. Полной поверхностьюобобщённого цилиндра называется фигура, состоящая из боковой поверхности и двух его оснований. | Через понятие цилиндрической поверхности 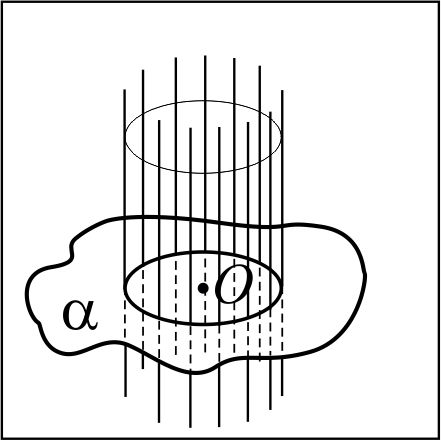 В некоторой плоскости α рассмотрим окружность ω(O, R) с центром в точке О и радиуса R. Через каждую точку окружности ω(O, R) проведём прямую, перпендикулярную к плоскости α. Фигура, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые – образующими цилиндрической поверхности. В некоторой плоскости α рассмотрим окружность ω(O, R) с центром в точке О и радиуса R. Через каждую точку окружности ω(O, R) проведём прямую, перпендикулярную к плоскости α. Фигура, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые – образующими цилиндрической поверхности. |
Цилиндр вращения (прямой круговой цилиндр) – тело вращения, полученное в результате вращения прямоугольника вокруг прямой, содержащей его сторону. Пусть прямоугольник ABCD вращается вокруг прямой BC, тогда ломаная BADC описывает поверхность цилиндра, отрезок AD – его боковую поверхность, а отрезки AB и DC – его основания. 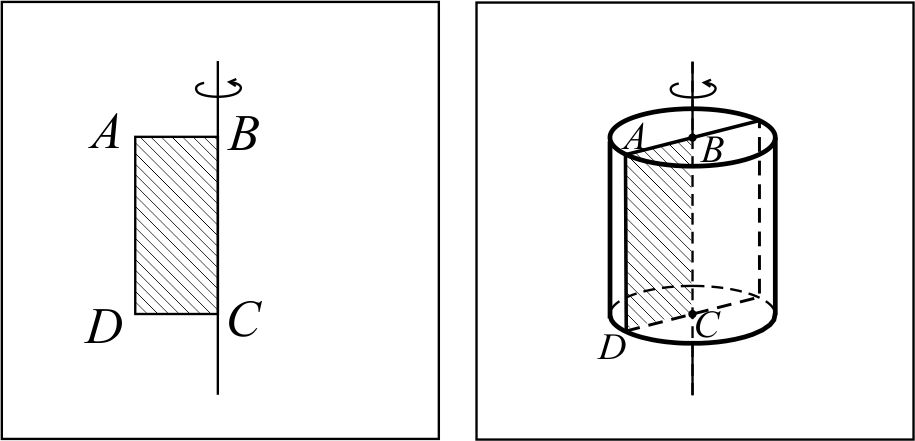 | Прямой круговой цилиндр – обобщённый цилиндр, основаниями которого являются круги, расположенные так, что их плоскости перпендикулярны прямой, проходящей через центры оснований. Прямая, проходящая через центры оснований цилиндра, называется осью прямого кругового цилиндра, радиусы кругов – радиусом прямого кругового цилиндра. 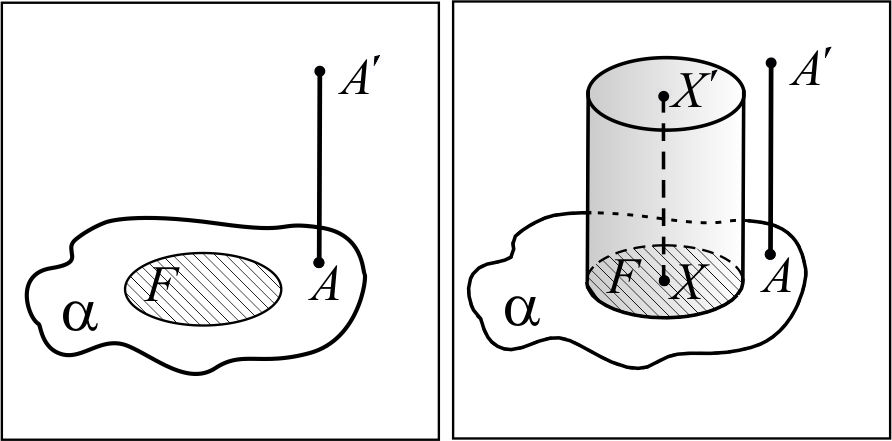 | Прямой круговой цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями, которые перпендикулярны образующим цилиндрической поверхности. 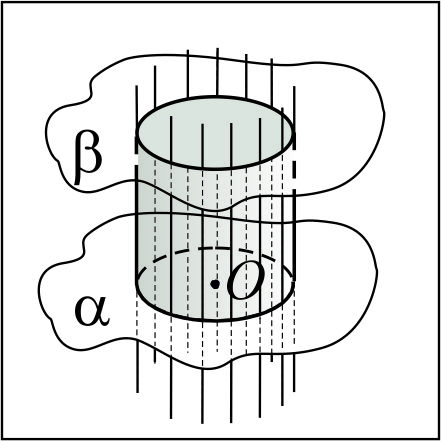 Круги, отсекаемые цилиндрической поверхностью от этих плоскостей, называются основаниями цилиндра. Часть цилиндрической поверхности, которая расположена между этими плоскостями, называется боковой поверхностью цилиндра. Отрезки образующих цилиндрической поверхности, расположенные между плоскостями оснований цилиндра, называются образующими цилиндра. Прямая, проходящая через центры оснований цилиндра, называется осью цилиндра, длина его образующей – высотой цилиндра, а радиус его основания – радиусом цилиндра. Круги, отсекаемые цилиндрической поверхностью от этих плоскостей, называются основаниями цилиндра. Часть цилиндрической поверхности, которая расположена между этими плоскостями, называется боковой поверхностью цилиндра. Отрезки образующих цилиндрической поверхности, расположенные между плоскостями оснований цилиндра, называются образующими цилиндра. Прямая, проходящая через центры оснований цилиндра, называется осью цилиндра, длина его образующей – высотой цилиндра, а радиус его основания – радиусом цилиндра. |
Первый подход используется в учебном пособии Л.А. Латотина и Б.Д. Чеботаревского; второй – в российском пособии [3] и в учебном пособии И.Ф. Шарыгина; третий подход – в учебных пособиях В.В. Шлыкова, Л.С. Атанасяна.
В школе рассматриваются только прямые круговые цилиндры. Для краткости их называют цилиндрами.
Свойства цилиндра:
· Основания цилиндра лежат в параллельных плоскостях.
· Образующие цилиндра параллельны и равны между собой.
· Развёрткой боковой поверхности цилиндра является прямоугольник.
Теорема(о площади боковой поверхности цилиндра).
…
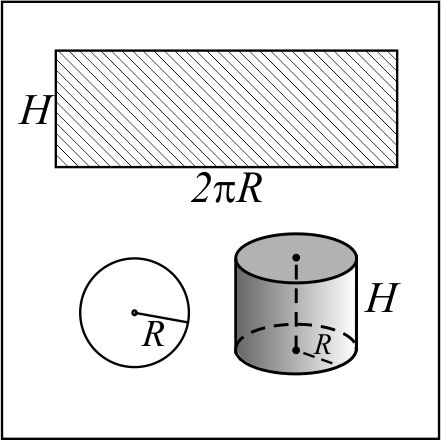
Иначе к этой формуле можно прийти, рассмотрев развёртку боковой поверхности цилиндра:
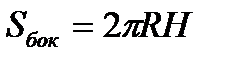
Теорема(об объёме цилиндра).
…
Сечения цилиндра плоскостью
При решении задач школьного курса геометрии рассматривают два вида сечений цилиндра плоскостью:
· 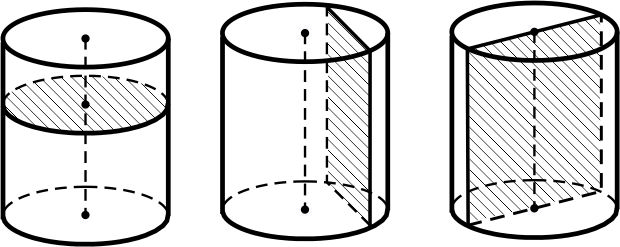 сечения, перпендикулярные оси цилиндра – круги;
сечения, перпендикулярные оси цилиндра – круги;
· сечения, параллельные оси цилиндра или проходящие через его ось – прямоугольники.
Сечение цилиндра плоскостью, проходящей через его ось, называется осевым сечением. Если осевым сечением цилиндра является квадрат, то цилиндр называют равносторонним.
Виды сечений цилиндрической поверхности плоскостью:
· сечение, перпендикулярное образующим – окружность;
· сечение, параллельное образующим – пара параллельных прямых;
· сечение, не перпендикулярное и не параллельное образующим – эллипс, т.е. множество точек плоскости, сумма расстояний от которых до двух заданных точек плоскости, называемых фокусами, есть величина постоянная.
Докажем это утверждение.
Утверждение 1. Сечение цилиндрической поверхности, не параллельное и не перпендикулярное образующей цилиндра – эллипс.
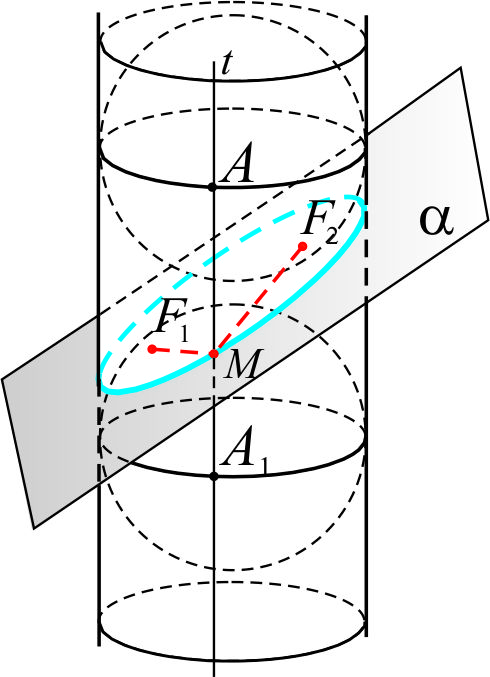 Пусть плоскость α, не параллельная и не перпендикулярная образующей цилиндра, пересекает поверхность цилиндра по некоторой линии l. Докажем, что эта линия – эллипс.
Пусть плоскость α, не параллельная и не перпендикулярная образующей цилиндра, пересекает поверхность цилиндра по некоторой линии l. Докажем, что эта линия – эллипс.
Рассмотрим два шара, которые касаются боковой поверхности цилиндра и плоскости α. Пусть точки F1 и F2 – точки касания. Через произвольную точку M линии l проведём образующую t. Пусть длина отрезка AA1 этой образующей, заключённого между диаметральными плоскостями шаров, перпендикулярными образующим цилиндра, равна 2a. Тогда по свойству касательных,
MF1 = MA1
+ MF2 = MA
MF1+MF2=MA1+MA=2a, т.е. MF1+MF2= const, значит, линия l – эллипс.Š
2.3. Конус. Боковая поверхность конуса. Объём конуса. Сечения конуса. Сечения конической поверхности
Можно выделить три подхода к определению понятия конуса:
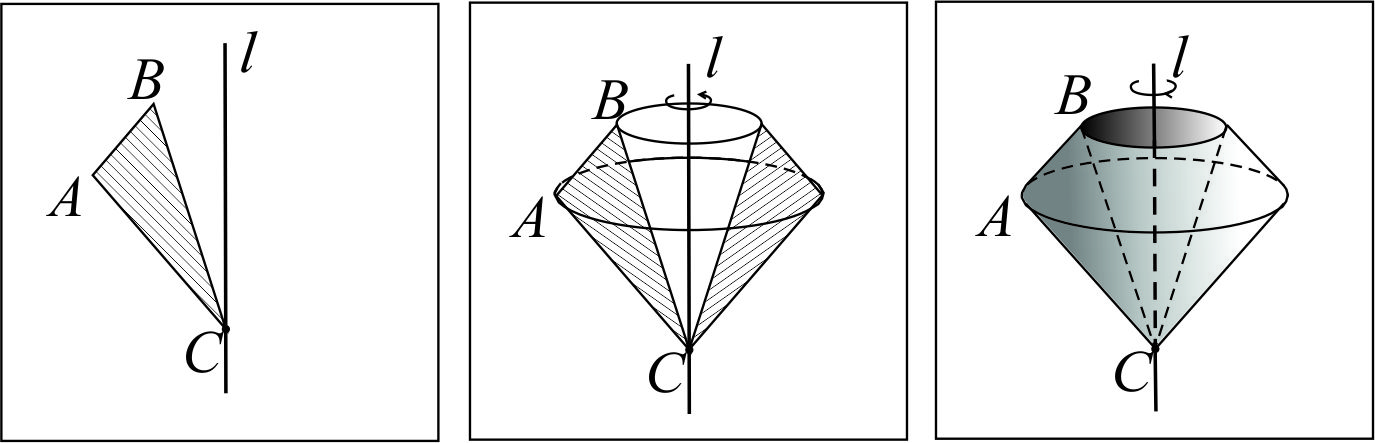
Через понятие тела вращения Тело вращения –фигура вращения, полученная в результате вращения геометрической фигуры вокруг прямой, лежащей в плоскости этой фигуры, обладающая всеми свойствами геометрического тела.  | Через понятие обобщённого конуса 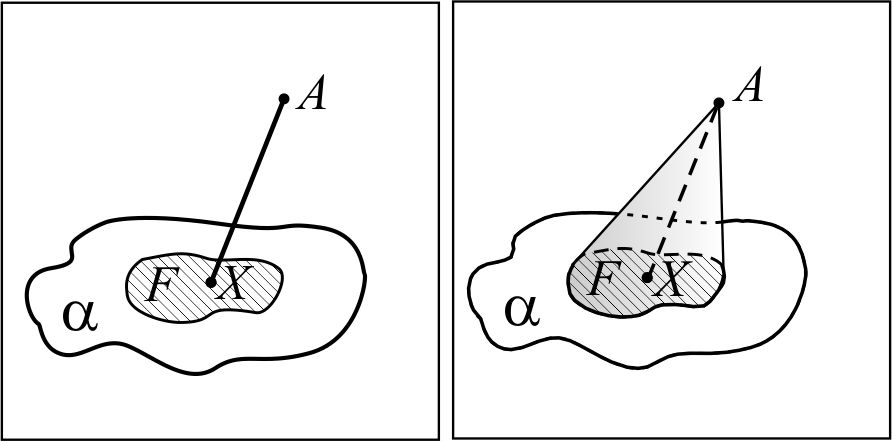 Рассмотрим фигуру F, лежащую в некоторой плоскости α и точку A вне этой плоскости. Из каждой точки X фигуры F проведём отрезок XA. Фигура, образованная всеми отрезками XA, называется обобщённым конусом. Фигура F называется основанием обобщённого конуса, точка A – его вершиной. Перпендикуляр, проведённый из вершины конуса к плоскости его основания, называется высотой обобщённого конуса. Если точка X отрезка AX принадлежит границе фигуры F, то отрезок AX называется образующей обобщённого конуса. Фигура, состоящая из всех образующих, называется боковой поверхностью обобщённого конуса. Полной поверхностью обобщённого конуса называется фигура, состоящая из боковой поверхности и его основания. Рассмотрим фигуру F, лежащую в некоторой плоскости α и точку A вне этой плоскости. Из каждой точки X фигуры F проведём отрезок XA. Фигура, образованная всеми отрезками XA, называется обобщённым конусом. Фигура F называется основанием обобщённого конуса, точка A – его вершиной. Перпендикуляр, проведённый из вершины конуса к плоскости его основания, называется высотой обобщённого конуса. Если точка X отрезка AX принадлежит границе фигуры F, то отрезок AX называется образующей обобщённого конуса. Фигура, состоящая из всех образующих, называется боковой поверхностью обобщённого конуса. Полной поверхностью обобщённого конуса называется фигура, состоящая из боковой поверхности и его основания. | Через понятие конической поверхности 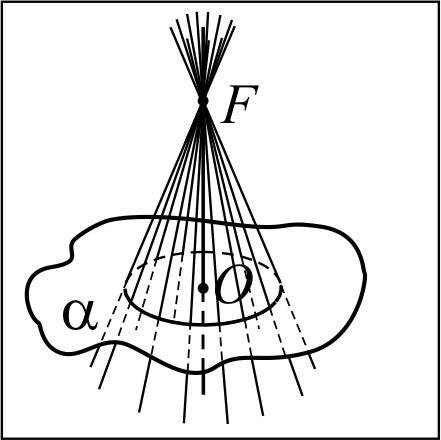 В некоторой плоскости α рассмотрим окружность ω(O, R) с центром в точке О и радиуса R и прямую FO (FÏα), которая перпендикулярна плоскости α. Через F и каждую точку окружности ω(O, R) проведём прямую. Фигура, образованная этими прямыми, называется конической поверхностью, сами прямые – образующими конической поверхности; прямая FO – осью конической поверхности. В некоторой плоскости α рассмотрим окружность ω(O, R) с центром в точке О и радиуса R и прямую FO (FÏα), которая перпендикулярна плоскости α. Через F и каждую точку окружности ω(O, R) проведём прямую. Фигура, образованная этими прямыми, называется конической поверхностью, сами прямые – образующими конической поверхности; прямая FO – осью конической поверхности. |
Конус вращения (прямой круговой конус) – тело вращения, полученное в результате вращения прямоугольного треугольника вокруг прямой, содержащей один из его катетов. Пусть прямоугольный треугольник ABC вращается вокруг прямой AC, тогда ломаная ABC описывает поверхность конуса, отрезок AB – его боковую поверхность, а отрезок BC – его основание. 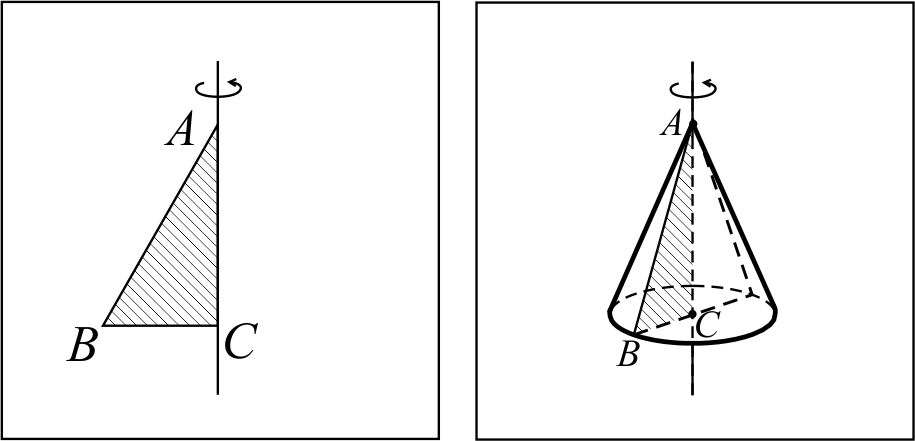 | Обобщённый конус, основанием которого является круг, называют круговым конусом. Прямым круговым конусом называют круговой конус, высота которого проецируется в центр круга. Прямая, проходящая через вершину и центр основания, называется осью прямого кругового конуса, радиус основания – радиусом прямого кругового конуса. 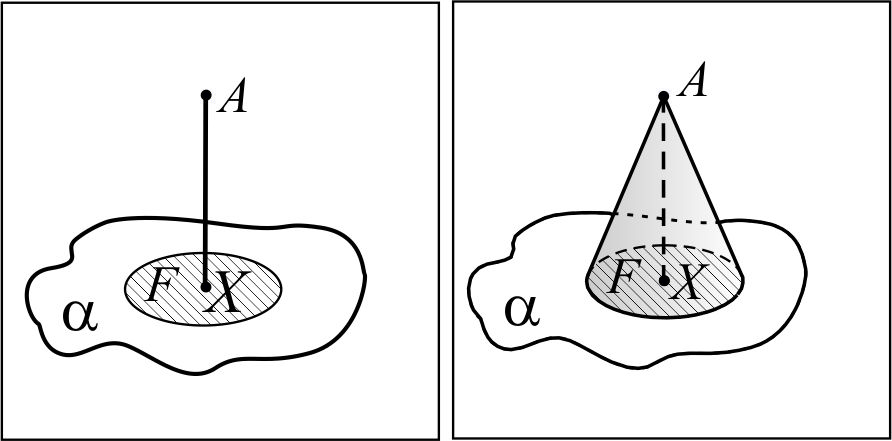 | Прямой круговой конус – геометрическое тело, ограниченное конической поверхностью и плоскостью, перпендикулярной оси этой поверхности. 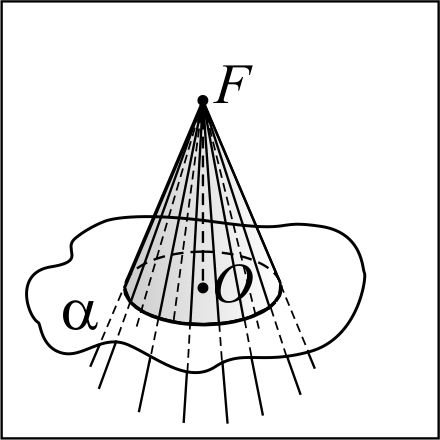 Круг, отсекаемый конической поверхностью от этой плоскости, называется основанием конуса, точка F – вершиной конуса. Отрезки конической поверхности, расположенные между вершиной и основанием конуса, называются образующими конуса. Фигура, образованная всеми образующими конуса, называется боковой поверхностью конуса. Прямая, проходящая через вершину и центр основания конуса, называется осью конуса, длина отрезка, концами которого служат вершина и центр основания конуса – высотой конуса, а радиус его основания – радиусом конуса. Круг, отсекаемый конической поверхностью от этой плоскости, называется основанием конуса, точка F – вершиной конуса. Отрезки конической поверхности, расположенные между вершиной и основанием конуса, называются образующими конуса. Фигура, образованная всеми образующими конуса, называется боковой поверхностью конуса. Прямая, проходящая через вершину и центр основания конуса, называется осью конуса, длина отрезка, концами которого служат вершина и центр основания конуса – высотой конуса, а радиус его основания – радиусом конуса. |
В школе рассматриваются только прямые круговые конусы. Для краткости их называют конусами.
Теорема(о площади боковой поверхности конуса).
…
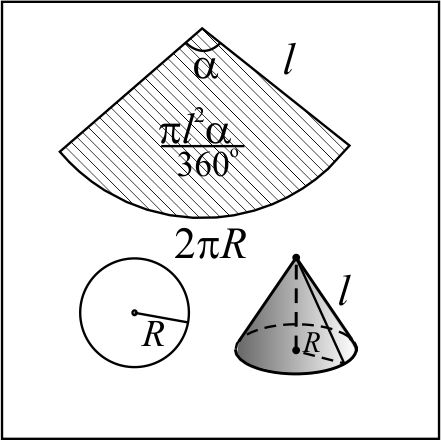 Иначе к этой формуле можно прийти, рассмотрев развёртку боковой поверхности конуса:
Иначе к этой формуле можно прийти, рассмотрев развёртку боковой поверхности конуса:
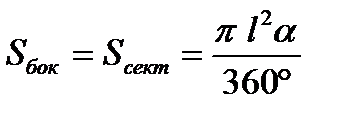 . Выразим угол α через радиус конуса и длину его образующей.
. Выразим угол α через радиус конуса и длину его образующей.
С одной стороны длина дуги сектора равна 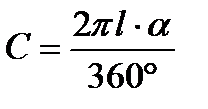 =
= 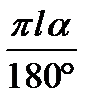 . С другой стороны, она равна длине окружности основания конуса:
. С другой стороны, она равна длине окружности основания конуса: 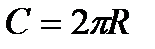 . Из уравнения
. Из уравнения 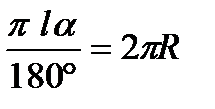 находим
находим 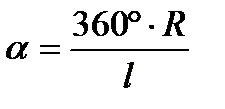 , тогда
, тогда 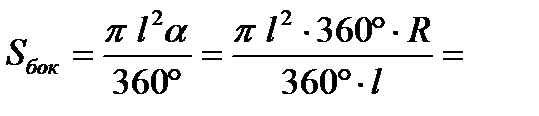
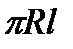 .
. 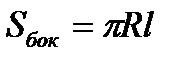
Теорема(об объёме конуса).
…
