Задачи для самостоятельного решения. а) Вычислить расстояние от прямой 2х - у + 1 = 0 до начала координат и до точки М(-1, 2).

а) Вычислить расстояние от прямой 2х - у + 1 = 0 до начала координат и до точки М(-1, 2).

б) В треугольнике с вершинами А(1, 2), В(2, -2), С(6, 1) найти:

1) уравнение стороны АВ;

2) уравнение высоты, проходящей через вершину С, и вычислить ее длину;

3) найти угол между этой высотой и медианой, проходящей через точку В.

в) Даны две вершины треугольника А(-10, 2) и B(6, 4); его высоты пересекаются в точке М(5, 2). Определить координаты третьей вершины С.

ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

Плоскость в пространстве

При рассмотрении плоскости в пространстве необходимо иметь в виду, что методика решения задач аналогична методике решения задач на прямую в плоскости. Это связано с тем, что различные уравнения плоскости в пространстве подобны уравнениям прямой на плоскости.

Приведем уравнения плоскости в пространстве:

- общее уравнение плоскости

- Ах + Ву + Сz + D = 0, (9.1)

где 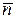= (А, В, С) – вектор, ортогональный плоскости (вектором нормали);

-уравнение плоскости в отрезках

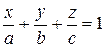, (9.2)

где 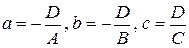, причем (а, 0, 0), (0, в, 0), (0, 0, с) - координаты точек пересечения плоскости с осями координат;

- уравнение плоскости, проходящей через точку (х₀, у₀, z₀) с вектором нормали 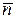= (А, В, С)

А(х - х₀) + В(у - у₀) + С(z - z₀) = 0, (9.3)

- нормальное уравнение плоскости

хcos a + уcos b + zcos g - p = 0, (9.4)

где р - расстояние от плоскости до начала координат, a, b, g - углы между координатными осями и вектором нормалью к плоскости, направленным от начала координат к плоскости;

- уравнение плоскости, проходящей через три точки (х₁, у₁, z₁), (х₂, у₂, z₂),

(х₃, у₃, z₃)

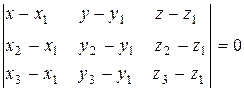(9.5)

Приведение общего уравнения плоскости (9.1) к нормальному виду (9.4) осуществляется домножением на множитель:

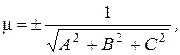
где знак выбирается из условия mD<0.

Расстояние d от точки (х₀, у₀, z₀) до плоскости (9.1) вычисляется по формуле:

d = 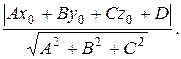(9.6)

Угол между плоскостями А₁х + В₁у + С₁z + D₁ = 0 и

А₂х + В₂у + С₂z + D₂ = 0 определяется из формулы:

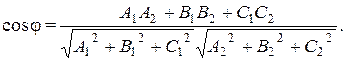(9.7)

Условие параллельности плоскостей:

А₁/А₂ = В₁/В₂ = С₁/С₂, (9.8)

и условие ортогональности:

А₁А₂ + В₁В₂ + С₁С₂ = 0. (9.9)

Примеры.

а) Приведем уравнение плоскости 2х + 4у - 5z + 21 = 0 к нормальному виду.

Домножив уравнение на нормирующий множитель

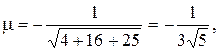
где знак минус взят, так как D>0, получим нормальное уравнение плоскости в виде

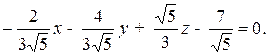
б) Составим уравнение плоскости, проходящей через точку (1, 2, 3) и ортогональную вектору (3, 2, 1).

Из уравнения (9.3) и геометрического смысла коэффициентов уравнения сразу имеем 3(х - 1) + 2(у - 2) + (z - 3) = 0 или

3х + 2у + z - 10 = 0.

в) Найдем уравнение плоскости, проходящей через точку (3, 2, -1) и параллельную плоскости 3х - 5у + 2z - 10 = 0.

В силу параллельности плоскостей векторы нормали у обеих плоскостей можно взять равными, т.е. вектор (3, -5, 2) является вектором нормали нашей плоскости. Тогда из уравнения (9.3) имеем

3(х - 3) - 5(у - 2) + 2(z + 1) = =0 или 3х - 5у + 2z + 3 = 0.

г) Найдем уравнение плоскости, проходящей через точки А(2, -1, 4) и В(3, 2, -1) перпендикулярно плоскости х + у + 2z - 3 = 0.

Для нахождения уравнения заданной плоскости нам необходимо найти вектор нормали 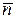этой плоскости. Так как он ортогонален нашей плоскости, то он ортогонален любому вектору, параллельному этой плоскости. Таким образом, вектор нормали 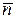ортогонален векторам 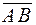и вектору нормали плоскости х + у + 2z - 3 = 0, т.е. 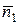= (1, 1, 2). Из свойств векторного произведения вытекает, что в качестве вектора нормали нашей плоскости можно взять вектор 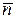= 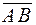´ 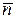₁.

Итак,

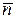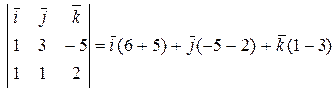= = (11, -7, -2).

Из (9.3) теперь легко имеем 11(х - 2) - 7(у + 1) - 2(z - 4) = 0 или

11х - 7у - 2z -21 = 0.

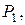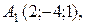
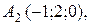
д) Найти угол между плоскостью проходящей через точки 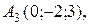и плоскостью 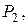заданной уравнением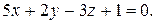

Взяв текущую точку 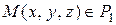и определив вектора 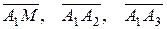, уравнение плоскости 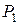находим по формуле (9.5):

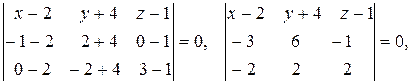
т.е.

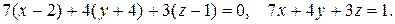
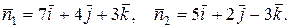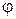По уравнению плоскостей определяем их нормальные векторы: Угол между плоскостям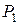и и 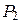находим по формуле (9.7):

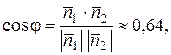
откуда 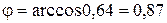рад.