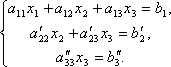Называется определителем системы.

Вопрос 7.

Рассмотрим квадратную матрицу:

Обозначим D =det A.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если D = 0.

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Свойства:

Определитель обратной матрицы равен обратной величине определителя исходной матрицы

2. 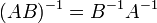для любых обратимых матриц А и В

3. 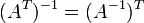, где Т-транспонированная матрица

4. 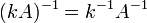, при любом к, не равном 0

Вопрос 8.

Ранг матрицы - наибольший из порядков ее миноров не равных нулю. Ранг матрицы А обозначают одним из символов: rang А, r. Если все миноры матрицы равны нулю, то ранг ее считается равным нулю.

Из определения ранга матрицы получаем следующие утверждения:

Ранг матрицы определяется целым числом, заключенным между 0 и меньшим из чисел m, n.

Ранг матрицы равен нулю, если матрица нулевая.

3. Для квадратной матрицы n-го порядка r = n тогда и только тогда, когда матрица невырожденная.

Свойства ранга:

Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы.

Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец.

Вопрос 9.

Системой m линейных уравнений с n неизвестными называется система вида

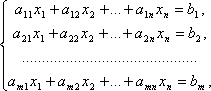
Коэффициенты при неизвестных будем записывать в виде матрицы, которую назовём матрицей системы:

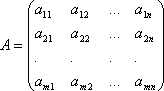
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.

Система может иметь одно решение.

Иметь бесконечное множество решений(записывается общее и частное решение)

Не иметь решений.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Вопрос 10.

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

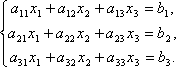
Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов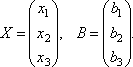

Найдем произведение

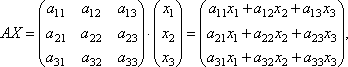
Это левая часть системы уравнений. В итоге получается

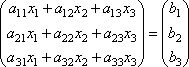
Или АХ=В, откуда Х находится, как X = A-1B.

Вопрос 11.

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

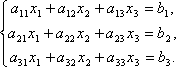
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

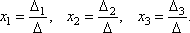
Вопрос 12.

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

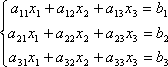
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:

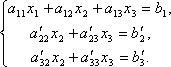
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

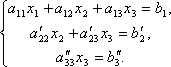
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.