Уравнения состояния и выхода соединений

МНОГОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ

ВОЗДЕЙСТВИЯХ

1.2.1. Описание сигналов и систем

1. Описание сигналов. Входные, выходные и промежуточные детермини­рованные сигналы в многомерных системах представляются вектор-функциями времени, например:

, ,

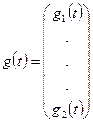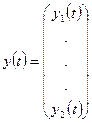где 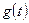— 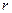-мерный входной, a 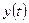— 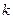-мерный выходной сигналы. В качестве компонент входного сигнала 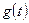могут использоваться единичные ступенчатые функции (1.2) и дельта-функции (1.1).

2. Описание систем. Многомерныелинейные нестационарные системы в от­личие от одномерных имеют 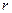входов и 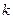выходов (рис. 1.16). Они описываются уравнениями состояния вида

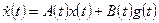(1.35)

С начальными условиями

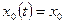(1.36)

И уравнениями выхода

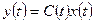, (1.37)

где 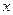— 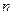-мерный вектор состояния; 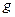— 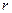-мерный вектор входных воздействий (управлений); 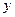— 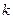-мерный вектор выхода (вектор измерений); 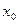— начальное ан-тояние; 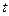— время; 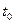— начальный момент времени (момент подачи входного воздействия); 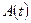, , 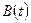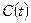— матрицы размера 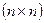, , 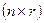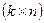соответственно.

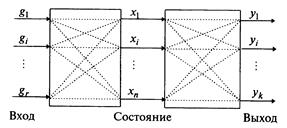
Рис. 1.16

Многомерную систему можно рассматривать как совокупность 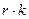одномерных систем, каждая из которых связывает один из 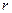входов с одним из 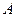выходов. Есл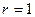и и 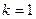, система является одномерной. Если матрицы 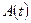, , 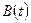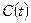не зависят от времени 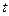, система называется многомерной стационарной.

Пример 1.15. Записать уравнения состояния и выхода многомерной системы:

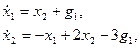
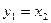
в матричной форме.

□ Определяем размерности сигналов: 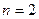, , 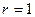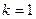и записываем соответствующие уравнения:

, .

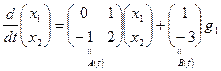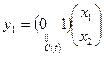Пример 1.16. Записать уравнения состояния и выхода многомерной системы

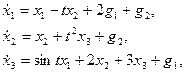
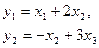
в матричной форме.

□ Определяем размерности сигналов: 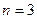, , 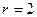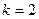и записываем соответствующие уравнения:

, .

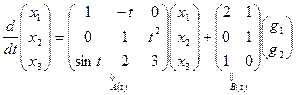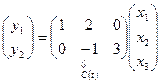Пример 1.17. Записать уравнения состояния и выхода многомерной системы:

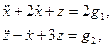
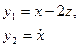
в матричной форме.

□ Обозначим 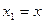, , 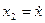, 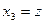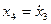. Тогда уравнения можно переписать в виде

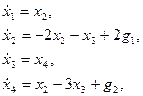
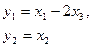
или в матричной форме ( , , ):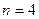

, .

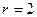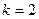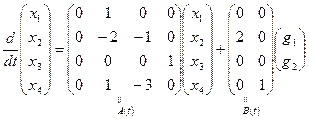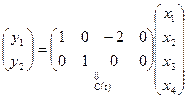Уравнения состояния и выхода соединений

Как следует из разд. 1.2.1, многомерная система, описываемая уравнения­ми состояния и выхода, полностью характеризуется набором трех матриц: 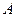, , 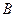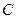. Здесь и далее аргумент 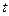для сокращения записи опущен. Две многомерные системы могут образовывать три типа соединений: параллельное, последователь­ное и с обратной связью, изображенные на рис. 1.17,а — в.

Предполагается, что обе системы, образующие соединения, описываются в пространстве состояний соотношениями:

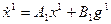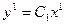, , (1.38)

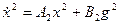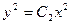, , (1.39)

где 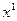, , 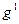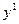— векторы состояния, входного сигнала и выхода первой системы размерности 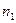, , 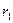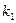соответственно; 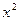, , 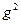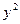— векторы состояния, входного сигнала и выхода второй системы, размерности которых 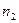, , 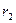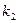соответ­ственно.

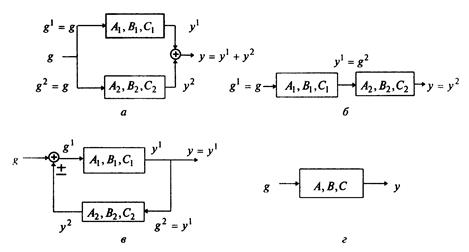
Рис. 1.17

Требуется заменить соединение эквивалентной системой, описываемой уравнениями (1.35), (1.37) и изображенной на рис. 1.17, г, в которой 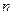, , 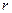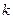—размерности векторов состояния 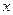, входного сигнала 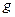и выхода .

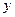1. Параллельное соединение (рис. 1.17, а). Условия соединения:

, , , .

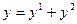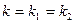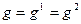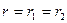Перепишем соотношения (1.38), (1.39) с учетом того, что :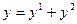

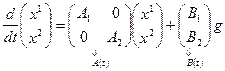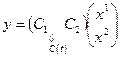, (1.40)

Полагая 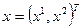, 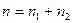и сравнивая с (1.35), (1.37), получаем матрицы

, ,

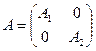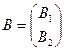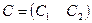
эквивалентной системы размера 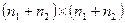, , 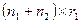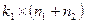соответственно.

Пример 1.18. Системы, образующие параллельное соединение, описывают­ся уравнениями:

первая система:

, ,

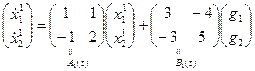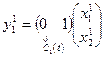где , , ;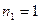

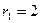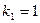вторая система:

, ,

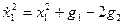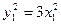где , , , , , .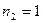

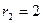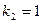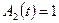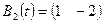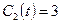Требуется записать уравнение эквивалентной системы.

□ Условия соединения 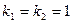, 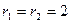выполняются. Согласно (1.40) эквивалентная система имеет вид

, ,

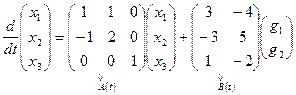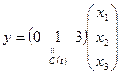где , , .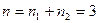

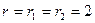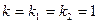2. Последовательное соединение (рис. 1.17,б). Условие соединения 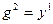, 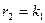. В первом соотношении (1.39) учтем, что 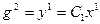, а из сравнения рис. 1.17,б и 1.17,г, получаем: 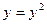, , 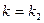, 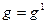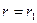. Эквивалентная сис­тема имеет вид

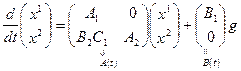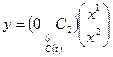, (1.41)

Полагая матрицы 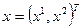, 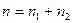и сравнивая с (1.35), (1.37), получаем

, ,

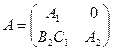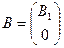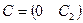
эквивалентной системы размера 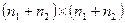, , 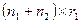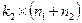соответственно.

Пример 1.19. Системы, образующие последовательное соединение, описы­ваются уравнениями: первая система:

, ,

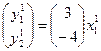где , , , , , ;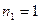

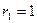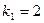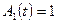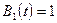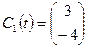вторая система:

, ,

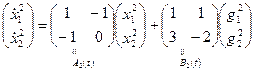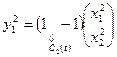где , , .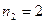

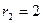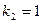Требуется записать уравнения эквивалентной системы.

□ Условие соединения 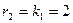выполняется. Согласно (1.41) эквива­лентная система имеет вид

, ,

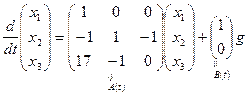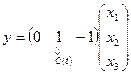где , , , .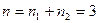

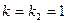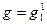3. Соединение с обратной связью (рис. 1.17, в). Условия соединения: 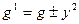, , 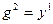, 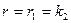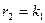. В первом соотношении (1.38) положим 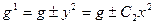, а в первом уравнении (1.39) 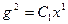. Сравнивая рис. 1.17, в и 1.17, г, получаем 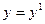. Эквивалентная система имеет вид

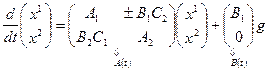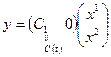, . (1.42)

Полагая 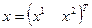, 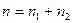и сравнивая с (1.35), (1.37), получаем матрицы

, ,

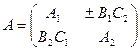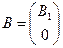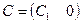
эквивалентной системы размера 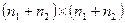, , 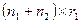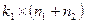соответственно. Знак «плюс» — для положительной, а знак «минус» — для отри­цательной обратной связи.

Пример 1.20. Системы, образующие соединение с отрицательной обратной связью, описываются уравнениями первая система

, ,

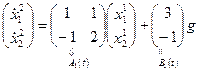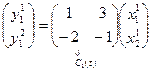где , , ;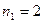

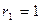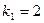вторая система:

, ,

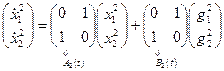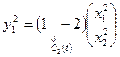где , , .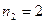

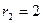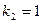Требуется записать уравнения жвивалентной системы.

□ Условия соединения 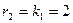, 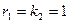выполняются. Согласно (1.42) эквивалентная система имеет вид

, ,

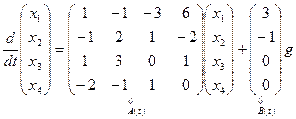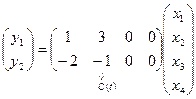где 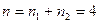, , .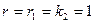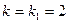