Модель управления запасами при вероятностном спросе и мгновенных поставках
Рассмотрим некоторые задачи управления запасами при вероятностном спросе. Простейшим случаем управления запасами является однократное принятие решений на пополнение запасов [І8]. Рассмотрим этот вариант.
I вариант. Рассмотрим модель управления запасами при вероятностном спросе и мгновенных поставках. Пусть 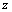 - запас продукта к началу операции;
- запас продукта к началу операции; 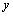 - запас после пополнения (
- запас после пополнения ( 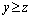 ), а (
), а ( 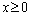 ) - случайный спрос за время операции
) - случайный спрос за время операции 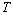 ;
; 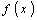 - плотность распределения спроса;
- плотность распределения спроса; 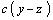 - расходы на пополнение запасов.
- расходы на пополнение запасов.
Предположим, что заказ на пополнение выполняется мгновенно. Если к концу операции на складе остается часть невостребованного запаса 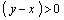 , то система снабжения несет расходы на сохранение избыточного запаса
, то система снабжения несет расходы на сохранение избыточного запаса 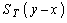 (при
(при 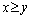 ,
, 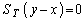 ). Наоборот, при неполном удовлетворении спроса (
). Наоборот, при неполном удовлетворении спроса ( 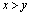 ) система платит штраф за дефицит
) система платит штраф за дефицит 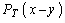 . Тогда математическое ожидание суммарных расходов системы за период равно
. Тогда математическое ожидание суммарных расходов системы за период равно
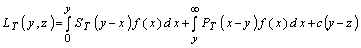 . (7.3.28)
. (7.3.28)
Найдем, при каких значениях 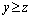 величина
величина 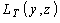 будет минимальной. Для этого определим
будет минимальной. Для этого определим
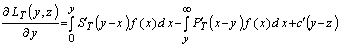 , (7.3.29)
, (7.3.29)
где 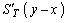 ,
, 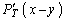 ,
, 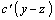 - обозначены частные производные по соответствующим функциям ( в (7.3.29) учтено, что
- обозначены частные производные по соответствующим функциям ( в (7.3.29) учтено, что 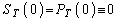 , и положим
, и положим 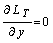 ).
).
В общем случае функция 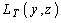 при фиксированных
при фиксированных 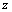 может иметь несколько минимумов.
может иметь несколько минимумов.
Обозначим через 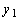 абсциссу абсолютного минимума
абсциссу абсолютного минимума 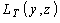 , а через
, а через 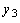 ,
, 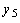 ,
, 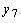 точки следующих относительных минимумов, причем пусть
точки следующих относительных минимумов, причем пусть 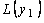 <
< 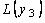 <
< 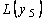 < .<
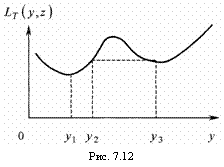
< .< 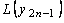 (рис. 7.12). Пусть далее
(рис. 7.12). Пусть далее 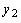 ,
, 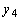 ,
, 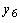 - точки, удовлетворяющие таким условиям:
- точки, удовлетворяющие таким условиям: 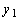 <
< 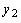 <
< 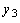 <
< 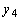 <.;
<.; 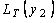 =
= 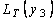 ,
,
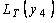 =
= 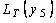 и т.д.
и т.д.
Тогда оптимальная стратегия управления запасами будет такой [18; 49]:
 при
при 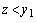 заказывать
заказывать 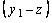 ;
;
при 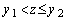 ничего не заказывать;
ничего не заказывать;
при 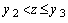 заказывать
заказывать 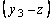 и т.д.
и т.д.
Приведем достаточные условия, при которых оптимальная стратегия имеет более простую форму, отвечающую одному минимуму функции 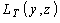 [49]:
[49]:
a) 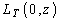 - не является относительным минимумом и
- не является относительным минимумом и
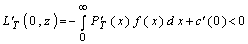 ;
;
в) уравнение 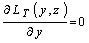 имеет не более одного вещественного корня;
имеет не более одного вещественного корня;
c) 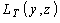 → ∞ при
→ ∞ при 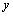 → ∞.
→ ∞.
Поясним физический смысл условий: а) экономическая целесообразность создания положительного запаса; с) неэффективность слишком больших запасов.
 Обозначим через
Обозначим через 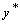 решение уравнения
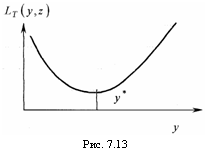
решение уравнения 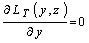 (рис. 7.13). Тогда оптимальная стратегия единственная и будет следующей:
(рис. 7.13). Тогда оптимальная стратегия единственная и будет следующей:
при 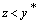 заказывать (делать заказа на поставку)
заказывать (делать заказа на поставку) 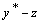 ;
;
при 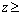
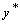 ничего не заказывать.
ничего не заказывать.
ІІ вариант. Допустим, что стоимость пополнения запасов равна 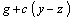 при
при 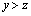 и нулю при
и нулю при 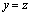 . Как видим, в этом случае в сравнении с вариантом І появился дополнительный член
. Как видим, в этом случае в сравнении с вариантом І появился дополнительный член 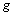 (фиксированная плата за заказ). В этом случае заказ целесообразно делать лишь при условии
(фиксированная плата за заказ). В этом случае заказ целесообразно делать лишь при условии
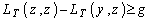 . (7.3.30)
. (7.3.30)
 Если уравнение (7.3.30) имеет единственное решение
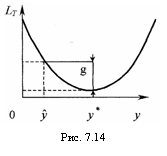
Если уравнение (7.3.30) имеет единственное решение 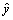 , то оптимальная стратегия, как видно из рис. 7.14, имеет вид [49]:
, то оптимальная стратегия, как видно из рис. 7.14, имеет вид [49]:
при 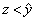 заказывать
заказывать 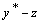 ;
;
при 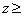
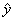 ничего не заказывать.
ничего не заказывать.
В литературе эта стратегия называется 'стратегией двух уровней' или (S,s)-стратегией [49].
