Системы линейных уравнений, методы их решения

Основные понятия

Рассмотрим систему m линейных уравнений с n неизвестными:

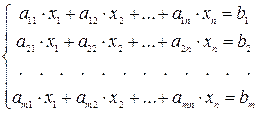(1)

x_j – неизвестное системы;

a_ij – коэффициент при неизвестном;

j = 1, n;

i = 1,m;

b_i – свободный член; i = 1, m.

Рассмотрим различные формы записи системы (1):

а) Краткая запись

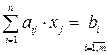(1`)

б) Матричная форма записи

Составим матрицу из коэффициентов при неизвестных:

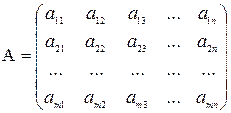
– основная матрица системы (1).

Составим матрицу-столбец неизвестных системы

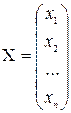
и матрицу-столбец свободных членов

Тогда матричная форма записи системы (1) имеет вид:

А ∙ Х = В

в) Векторная форма записи (1``)

Рассмотрим следующие векторы-столбцы системы (1) вида:

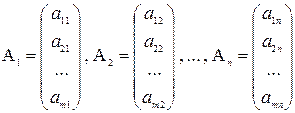
Х = (x₁, x₂, x₃, … , x_n) – n переменных.

Составим линейную комбинацию векторов условий вида:

А₁ ∙ х₁ + А₂ ∙ х₂ + … + А_n ∙ х_n

где х₁, х₂, … , х_n коэффициенты системы (1).

Линейная комбинация векторов – новый вектор, т.е. система (1) в векторной форме имеет вид:

А₁ ∙ х₁ + А₂ ∙ х₂ + … + А_n ∙ х_n = 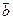(1```)

Решить систему линейных уравнений значит найти ее решения, или убедиться, что их нет.

Решением системы линейных уравнений (СЛУ) называется такой вектор
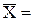(α₁; α₂; … ; α_n), координаты которого обращают в тождество каждое уравнение системы, если в каждое уравнение системы подставить вместо

Х₁ – α₁, Х₂ – α₂, … , Х_n – α_n.

Система уравнений называется совместной, если существует хотя бы одно решение (одно или ∞).

СЛУ называется несовместной, если она не имеет ни одного решения.

Совокупная система уравнений может иметь одно решение ( совместная и определенная) или бесконечное множество решений (совместная и неопределенная). Случай, когда решений конечное множество невозможен.

Две системы называются равносильными, если они имеют одни и те же решения.

Методы решения СЛУ

10.2.1 Решение системы с помощью обратной матрицы

Этот метод может быть применен для решения систем когда m = n. В этом случае основная матрица системы А – квадратичная порядка n.

Если при этом определитель |А| ≠ 0, т.е. квадратная матрица А – невырожденная, то она имеет единственную обратную матрицу.

Рассмотрим систему вида (1), записанную в матричной форме:

А ∙ Х = В

А^-1 ∙ А ∙ Х = А^-1 ∙ В

Е ∙ Х = А^-1 ∙ В

Х = А^-1 ∙ В

Х = (α₁; α₂; … ; α_n) – вектора решения

х₁ = α₁

х₁ = α₁

. . . . . .

х_n = α_n

10.2.2 Решение систем линейных уравнений с помощью определителей.

Применяется при условии m = n.

Составим определитель из коэффициентов при неизвестных системы линейных уравнений, у которой n уравнений и n неизвестных. Такой определитель называют основным определителем системы.

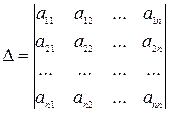
Составим вспомогательные определители для данной системы следующим образом:

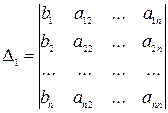
Δ₁ – определитель, который получается из основного определителя заменой его первого столбца столбцом свободных членов системы.

. . . . . . . . . . . . . . . . . . .

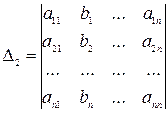
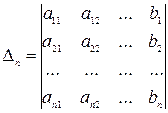
Неизвестные данной системы можно найти по формуле Крамера:

; ; … ; .

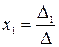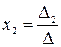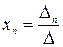1) Если основной определитель системы отличен от нуля, то такая система уравнений имеет единственное решение – она совместна и определенна, и это решения находят по формуле Крамера;

2) Если основной определитель системы равен нулю, то система уравнений может быть совместной неопределенной (∞ решений) или несовместной (не имеет решений):

а) Если основной определитель системы равен нулю и все вспомогательные определители равны нулю, то система уравнений имеет ∞ решений;

б) Если основной определитель системы равен нулю и хотя бы один из вспомогательных определителей не равен нулю, то система – несовместна.

Рассмотрим случай 2 а, т.е. Δ = 0; Δ₁, Δ₂, … , Δ_n = 0.

Тогда исключают одно из уравнений данной системы (оно является следствием других уравнений системы). Затем выделяют основные переменные (базисные) и свободные переменные, которые могут принимать любые значения из множества действительных чисел.

Если какие-то векторы полученной системы будут линейно независимыми, значит они образуют базис, а следовательно переменные при этих векторах также будут базисными.

Набор переменных, входящих в базис, может быть разным, а количество базисных переменных в каждом наборе – одно и то же.

Иначе за базисные переменные можно принять такие переменные, при которых определитель, составленный из коэффициентов при данных переменных, отличен от нуля.

После того, как выбраны базисные переменные, их выражают в рассматриваемой системе через свободные переменные. Полученная при этом СЛУ и будет являться общим решением исходной системы.

Если свободным переменным придавать любые значения из множества действительных чисел, то будем получать частные решения исходной системы в виде векторов, и таких векторов будет бесконечное множество.

Базисным решением исходной таблицы будет являться вектор, у которого все свободные переменные равны нулю, а базисные переменные равны свободным членам системы общего решения.

Базисное решение называется допустимым, если все координаты вектора базисного решения не отрицательны.

10.2.3 Решение СЛУ методом последовательного исключения переменных.

Этот метод основан на применении элементарных преобразований над системой уравнений, которые преобразуют данную систему уравнений в эквивалентную ей.

Различают два метода исключения переменных: метод Гаусса и метод Жордана – Гаусса (метод полного исключения переменных). Это универсальные методы решения систем линейных уравнений, т.к. их можно применять для решения систем в случае когда m = n и m ≠ n.

Рассмотрим метод Жордана – Гаусса.

Этот метод состоит из нескольких шагов (итераций), которые позволяют за конечное число операций сделать вывод о существовании решения данной системы или о том, что решений нет.

На каждом шаге исключается одна из переменных, которая называется ведущей. Ведущая переменная остается в одном из уравнений, которое также называется ведущим (ключевым). Из оставшихся уравнений ведущая переменная исключается с помощью элементарных преобразований.

Процесс исключения переменных производится с помощью таблиц Гаусса. Таблицей Гаусса обычно называют расширенную матрицу данной системы вида:

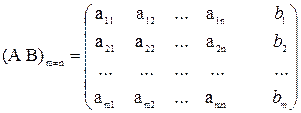
На основании элементарных преобразований над строками расширенной матрицы системы m линейных уравнений с n неизвестными, сформируем правила исключения переменных:

1) Выбираем ведущий элемент,то-есть ведущую строку, ведущий столбец.

Каждый элемент ведущей строки делим на ведущий элемент, и результат записываем в такую же по номеру строку новой (эквивалентной) матрицы;

2) Ведущий столбец в эквивалентной матрице превращается в единичный вектор;

3) Если в ведущей строке есть нули, то соответствующие столбцы переписываются без изменения;

4) Если в ведущем столбце есть нули, то соответствующие строки переписываются без изменения;

5) все остальные элементы эквивалентной матрицы находятся по правилу прямоугольника:

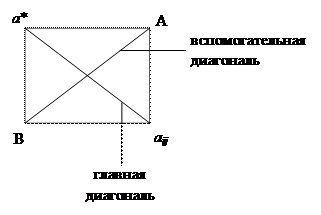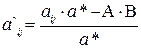
где a_ij – соответствующий элемент первой таблицы;

a`_ij – новый элемент эквивалентной таблицы;

a* –разрешающий элемент расширенной матрицы;

A – элемент расширенной матрицы, стоящий в ведущей строке;

B – элемент расширенной матрицы, стоящий в ведущем столбце.

6) Все предыдущие пункты повторяются шаг за шагом, пока:

а) либо основная матрица системы будет состоять из единичных векторов (СЛУ имеет единственное решение, она совместна и определенна);

б) либо на некотором шаге преобразованной матрицы в одной из строк все элементы превратятся в нули, и при этом не встретится строка вида:

(0 0 0 … 0 b), b ≠ 0, (*)

то строку из нулей вычеркивают, и система будет иметь бесконечное множество решений (она будет совместна и неопределенна).

В этом случае выделяют базисные и свободные переменные. Базисные переменные выражают через свободные, получают общее решение исходной системы, из которого можно получить бесконечное множество частных решений.

Базисное- это такие решение, когда все свободные переменные равны нулю, а базисные переменные принимают значения любых действительных чисел.

Если компоненты вектора базисного решения не отрицательны, то это базисное решение будет допустимым базисным решением (опорным решением данной системы).

в) либо на некотором шаге получим строку вида (*), тогда решение системы заканчивается, говорят, что система не совместна, не имеет решений.

Пример:

Решить СЛУ:

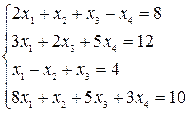
Применим метод Жордана – Гаусса.

Составим расширенную матрицу системы:

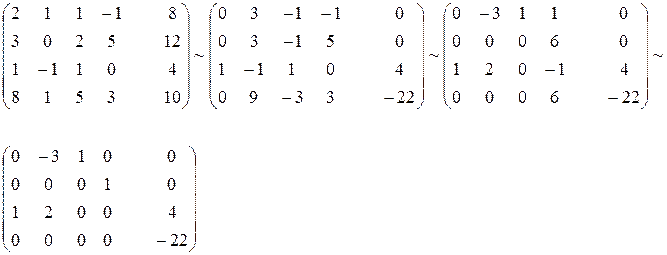
0 = -22 – неверно, следовательно система не совместна, не имеет решений.