Определение уравновешивающих сил и моментов методом Н. Е. Жуковского

Согласно принципу Даламбера все реально действующие на звенья механизма силы, дополненные уравновешивающими, а также инерционными силами и моментами, образуют равновесную систему.

Согласно принципу возможных перемещений для такой системы сумма мгновенных мощностей всех сил и моментов в любой момент времени (и в любом положении механизма) равна нулю. И, что особенно важно, при расчетах без учета трения, т.е. в случае идеальных связей, реакции в кинематических парах в этом балансе мощностей не уча­ствуют.

Мощность каждого момента вычисляют по формуле

, (4.14)

где – угловая скорость звена, к которому приложен вращающий момент (это может быть момент полезного сопротивления, инерционный и т.д.); мощность – величина алгебраическая, она положительна, если направления момента и угловой скорости совпадают.

Мощность силы , приложенной в точке, скорость которой равна (рис. 4.11, а) находят как скалярное произведение указанных векторов

. (4.15)

а б в

Рис. 4.11

Поскольку – модули соответствующих векторов, т.е. величины заведомо положительные, то знак мощности полностью определяется знаком величины или правилом: мощность положительна, если угол между векторами острый, и отрицательна, если этот угол тупой (очевидно, что мощность , если ).

Произведение представляет собой проекцию вектора (рис. 4.11, б); но тогда мощность, определяемую равенством (4.15), можно рассчитать как момент силы , повернутой относительно своего истинного направления на и приложенной к концу вектора , относительно начала этого вектора
(рис. 4.11, в), т.е.

; (4.16)

здесь имеет размерность скорости.

На равенстве (4.16) и основан метод Н. Е. Жуковского, реализация которого при вычислении уравновешивающих сил и моментов сводится к следующему (при условии, что план скоростей механизма уже построен в некотором масштабе ):

1) на плане скоростей отмечают точки приложения всех внешних сил (веса, инерции, полезного сопротивления);

2) к отмеченным точкам плана прикладывают соответствующие силы, повернутые на относительно их истинных направлений; направление поворота векторов сил может быть любым, но оно должно быть одинаковым для всех сил; для каждой «повернутой» силы измеряют ее плечо (в миллиметрах) относительно полюса плана ;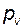

план скоростей с приложенными к указанным точкам силами интерпретируют как жесткий рычаг, шарнирно прикрепленный в полюсе 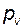к стойке; заметим, что результат выполненного построения называют «рычагом Н. Е. Жуковского»;

3) устанавливают правило знаков для выполненного построения; здесь нужно исходить из следующего:

· знак момента любой силы в рычаге Жуковского должен совпадать со знаком ее мощности;

· все силы, имеющие мощности одинакового знака, имеют в рычаге Жуковского моменты одинакового направления;

таким образом, правило знаков можно установить по любой одной силе, для которой знак мощности достоверно известен;

4) составляют уравнение, которое, например, для механизма с одной степенью свободы и вращающимся начальным звеном имеет вид

. (4.17)

Это уравнение имеет единственную неизвестную , которая легко определяется. Если полученное значение уравновешивающего момента положительно, то он направлен в сторону вращения начального звена.

4.8. Определение уравновешивающих сил и моментов методом, основанным на применении принципа
возможных перемещений

Предлагаемый аналитический способ расчета уравновешивающих сил и моментов использует ту же теоретическую основу, что и графо-аналитический метод Н.Е.Жуковского. Разница состоит в том, что здесь мощность любой силы рассчитывают по формуле

, (4.18)

где и − проекции на координатные оси векторов соответственно (мощности, развиваемые моментами, по-прежнему находят по формуле (4.14)).

Поскольку при аналитических расчетах все величины в (4.14) и (4.18) являются алгебраическими, то уравнение баланса мощностей для равновесной системы сил и моментов, действующих на звенья механизма, в самом общем случае принимает вид

; (4.19)

здесь g = 9.81 м/с² − ускорение силы тяжести; − проекции на координатные оси скоростей и ускорений центров масс звеньев; − проекции на координатные оси скорости точки приложения силы ; слагаемое учитывает мощность, развиваемую всеми силами веса, − инерционными силами, − инерционными моментами; − суммарная мощность силы и момента полезного сопротивления.

Значения , найденные методами планов сил и Н. Е. Жуковского должны незначительно отличаться от величины, найденной аналитическим методом (обычно величину допускаемой погрешности оговаривают в задании на курсовую или иную расчетную работу).

Вопросы для самопроверки

1. Назовите цели и методы силового анализа механизма.

2. Определите понятия «уравновешивающая сила», «уравновешивающий момент».

3. Сформулируйте условие статической определимости плоского механизма.

4. Почему всегда является статически определимой структурная группа?

5. Опишите последовательность силового анализа плоского механизма, подчиняющегося классификации Ассура.

6. Как найти уравновешивающий момент, не определяя реакций в кинематических парах?

7. С какой целью при силовом анализе механизма к его звеньям прикладывают инерционные силы и моменты (которые в действительности не являются реальными силами, действующими на эти звенья)?

Задачи

Задача 4.01 Для кинематической цепи рассчитать величину реакции в шарнире B от действия внешней силы . Заданы размеры звеньев:

точка C расположена посередине звена 3. Линия действия силы Q пер­пендику­лярна прямой AB, взаимное расположение звеньев 3 и 5 определяется углом .

	Задача 4.02 Для кинематической цепи рассчитать величину реакции в шарнире A от действия силы . Заданы размеры звеньев: . Линия действия силы Q пер­пендику­лярна прямой AC, взаимное расположение звеньев 3 и 4 определяется расстоянием .
	Задача 4.03 Для кинематической цепи рассчитать величину реакции в шарнире A от действия силы . Заданы размеры: ; взаимное распо­ложение направляющих 2 и 5 в текущем положении определяется углом . Линия действия силы Q пер­пендику­лярна прямой AB.
Задача 4.04(см. рисунок к задаче 4.03) Для кинематической цепи рассчитать величину реакции в поступательной паре (4-5) от действия силы . Заданы размеры: ; взаимное распо­ложение направляющих 2 и 5 в текущем положении определяется углом . Линия действия силы Q пер­пендику­лярна прямой AB.

Задача 4.05(см. рисунок к задаче 4.03) Для кинематической цепи рассчитать величину реакции в поступательной паре (2-3) от действия силы . Заданы размеры звеньев: ; взаимное распо­ложение направляющих 2 и 5 в текущем положении определяется углом . Линия действия силы Q пер­пендику­лярна прямой AB.
	Задача 4.06 Для кинематической цепи рассчитать величину реакции в шарнире B от действия силы . Заданы размеры звеньев: ; . Взаимное распо­ложение направляющей 5 и шатуна AB в текущем положении определяется углом . Линия действия силы Q направлена под углом к направляющей 5.
Задача 4.07(см. рисунок к задаче 4.06) Для кинематической цепи рассчитать величину реакции в шарнире A от действия силы . Заданы размеры звеньев: ; . Взаимное распо­ложение направляющей 5 и шатуна AB в текущем положении определяется углом . Линия действия силы Q направлена под углом к направляющей 5.
Задача 4.08(см. рисунок к задаче 4.06) Для кинематической цепи рассчитать величину реакции в поступательной паре (4-5) от действия силы . Заданы размеры звеньев: ; . Взаимное распо­ложение направляющей 5 и шатуна AB в текущем положении определяется углом . Линия действия силы Q направлена под углом к направляющей 5.
	Задача 4.09 Для кинематической цепи рассчитать величину реакции в шарнире B от действия силы . Задано соотношение длин . Взаимное распо­ложение прямых AB и BC в текущем положении определяется углом . Линия действия силы Q направлена перпендикулярно прямой AB.
Задача 4.10(см. рисунок к задаче 4.09) Для кинематической цепи рассчитать величину реакции в шарнире A от действия силы . Задано соотношение длин . Взаимное распо­ложение прямых AB и BC в текущем положении определяется углом . Линия действия силы Q направлена перпендикулярно прямой AB.
Задача 4.11(см. рисунок к задаче 4.09) Для кинематической цепи рассчитать величину реакции в шарнире С от действия силы . Задано соотношение длин . Взаимное распо­ложение прямых AB и BC в текущем положении определяется углом . Линия действия силы Q направлена перпендикулярно прямой AB.
Задача 4.12 Определить уравновешивающий момент , приложенный к звену 1, при следующих данных: звено 1 - вертикально, звено 3 - горизонтально, угол ; линия действия силы направлена перпендикулярно прямой AB, причем .

	Задача 4.13 Определить уравновешивающий момент , приложенный к звену 1 при следующих данных: звено 1 вертикально, звено 3 - горизонтально, угол ; линия действия силы направлена перпендикулярно прямой AB, причем .
Задача 4.14 Определить уравновешивающий момент , приложенный к звену 1 при следующих данных: звено 1 вертикально, звено 3 - горизонтально, угол ; линия действия силы направлена перпендикулярно прямой AB, причем .
	Задача 4.15 Какую силу Q способен преодолеть при равновесном состоянии механизма момент , приложенный к кривошипу 1 при . Размеры звеньев механизма: ; .
Задача 4.16(см. рисунок к задаче 4.15) Определить реакцию в шарнире B, возникающую при равновесном состоянии механизма, от момента , приложенного к кривошипу 1 при . Размеры звеньев механизма: ; .
Задача 4.17(см. рисунок к задаче 4.15) Считая состояние механизма равновесным, определить реакцию в поступательной паре, возникающую от момента , приложенного к кривошипу 1 при . Размеры звеньев механизма: ; .