Ионно-релаксационная поляризация

В диэлектриках, содержащих подвижные ионы при наложении постоянного электрического поля наблюдается их смещение в пределах параметра элементарной ячейки. Это создает неравномерность их распределения по объему образца и приводит к поляризации диэлектрика. Переходы ионов осуществляются под действием тепловой энергии. Вероятности перехода ионов по направлению поля и против поля различны и протекают в определенном временном интервале. Такие процессы относятся к релаксационным и характеризуются временем релаксации τ.

Релаксация - есть процесс постепенного изменения заданной физической величины с течением времени, приводящий к достижению равновесного значения заданного параметра.

Ионно-релаксационная поляризация возникает вследствие преимущественного переноса ионов по направлению поля. Рассмотрим ион, который в отсутствие внешнего электрического поля может находиться в кристалле в двух положениях равновесия с одинаковым минимумом потенциальной энергии (рис.)

-Рисунок 9.

Пусть расстояние между ионами соответствует параметру элементарной ячейки а. При включении электрического поля ион приобретает энергию qEa. При qEa << ΔU электрическое поле не может вызвать перехода иона из положения 1 в положение 2. Такие переходы оказываются возможными благодаря тепловому движению. Согласно соотношению Больцмана вероятность перехода из 1 в 2 путем преодоления потенциального барьера определяется величиной:

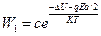, (68)

где с- постоянный коэффициент, а из положения 2 в1:

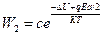, (69)

Если в единице объема находятся n₁ ионов в положении 1 и n₂ ионов в положении 2, то число переходов из 1 в 2 и из 2 в 1 за время dt равно:

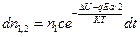, (70)

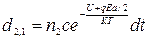. (71)

Изменение числа ионов в положении 1 определяется разностью:

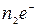
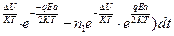, (72)

При равновесии 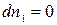и следовательно:

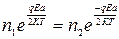, (73)

Интенсивные переходы из положения 1 в 2 и обратно происходят при равенстве тепловой энергии и величине потенциального барьера KT~ΔU. Поэтому при 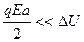следует считать 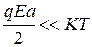. При этом условии экспоненты можно разложить в ряд.

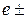
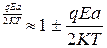, (74)

С учетом (74) соотношение (73) преобразуется следующим образом:

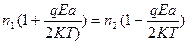, (75)

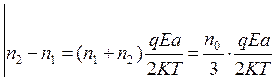, (76)

В (76) учтено, что в направлении поля перемещается лишь 1/3 всех перемещающихся ионов 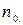и сумма (n₁+n₂₎ заменена на 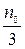. Когда из 1 в 2 переходит один ион с зарядом q, возникает электрический момент qa. При этом n₁ уменьшается на 1, n₂ увеличивается на 1 и следовательно n₂-n₁=2. Поэтому, когда из 1 в 2 переходят 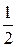(n₂-n₁) ионов возникает поляризация:

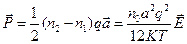, (77)

Сопоставляя полученное соотношение (77) с (8) можно оценить вклад в диэлектрическую проницаемость ионно-релаксационной поляризации.

, (78)

Из соотношения (78) следует, что 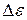уменьшается с ростом температуры. Этот результат на первый взгляд противоречит исходному предположению о тепловой активации ионной поляризации, однако, в конечном счете, температурное воздействие разупорядочивает направленное по полю смещение ионов.

Следует также учесть, что выражение для 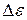получено из условия установившегося равновесия 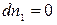. В тоже время общая поляризация диэлектрика будет зависеть от времени приложения внешнего электрического поля. Рассмотрим процесс установления равновесия. В этом случае .

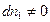Тогда, изменение концентрации ионов в положении 1 будет описываться дифференциальным уравнением:

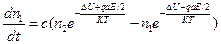, (79)

С учетом того, что 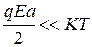используя соотношения (79) получим:

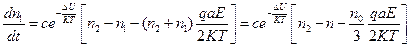, (80)

Так, как 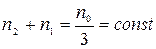, то первая производная концентрации по времени будет равна нулю, откуда следует:

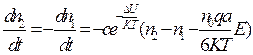, (81)

Изменение числа ионов в положении 1 и 2 за интервал времени описывается соотношением:

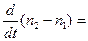
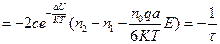
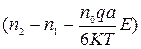(82),

где = 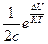- время релаксации.

Дифференциальное уравнение (82) имеет решение:

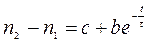
, (83)

где с и b - постоянные величины и могут быть найдены из начальных условий. Подставляя полученное решение (83) в (82) получим, что константа с имеет вид:

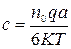, (84)

Постоянную 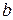определяем из начальных условий полагая, что в начальный момент времени при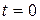

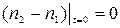, (85)

Экспонента в выражении при этих условиях равна единице и коэффициент b может быть вычислен по формуле:

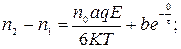(86)

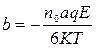, (87)

Используя соотношения (77), (86) и (87) получим выражение описывающее общую поляризацию диэлектрика

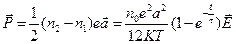, (88)

Из соотношения (86) вычислим изменение концентрации ионов в положении 1 и 2

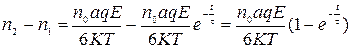, (89)

Подставляя (89) в (77) получим выражение для диэлектрической проницаемости, учитывающее изменение поляризации диэлектрика от времени приложения электрического поля:

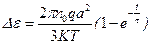, (90)