Понятие о корректно и некорректно поставленных задачах математической физики, примеры
Корректность - непрерывная зависимость решения от дополнительных условий в любой конечной точке области, т.е. если имеем уравнение 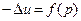 и два условия
и два условия 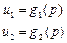 , причём
, причём 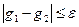 (отличные на малую величину), то и
(отличные на малую величину), то и 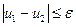 (тоже мало отличаются).
(тоже мало отличаются).
Пусть 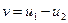 ,
, 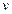 - гармоническая функция, тогда:
- гармоническая функция, тогда: 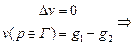
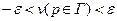 , тогда по теореме о максимумах и минимумах везде в области D верно:
, тогда по теореме о максимумах и минимумах везде в области D верно: 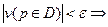
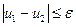
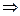 то есть малому изменению граничных условий отвечает малое изменение решений. Задача Дирихле корректна.
то есть малому изменению граничных условий отвечает малое изменение решений. Задача Дирихле корректна.
Пример некорректной задачи: 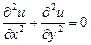 - уравнение Лапласа. Рассмотрим задачу Коши:
- уравнение Лапласа. Рассмотрим задачу Коши: 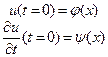 .
.
Рассмотрим два типа начальных условий: 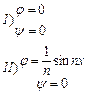 . Эти граничные условия мало отличаются при
. Эти граничные условия мало отличаются при 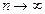 . Но решения не будут близкими при этом:
. Но решения не будут близкими при этом: 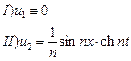 , т.к.
, т.к. 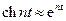 . Таким образом, решения будут существенно различны.
. Таким образом, решения будут существенно различны.
10. Уравнение с оператором 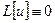 с особенностью
с особенностью 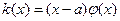 , свойства, ограниченность, постановка задачи.
, свойства, ограниченность, постановка задачи.
Теория специальных функция – это теория следующих уравнений: (*) 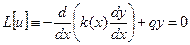 - линейное дифференциальное уравнение второго порядка. Пусть функция
- линейное дифференциальное уравнение второго порядка. Пусть функция  , т.е.
, т.е. 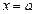 - нуль первого порядка. Решение (*) всегда:
- нуль первого порядка. Решение (*) всегда: 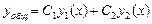 . Рассмотрим решение в окрестности особой точки, в которой
. Рассмотрим решение в окрестности особой точки, в которой 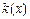 обращается в ноль.
обращается в ноль.
Теорема. Если уравнение 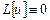 имеет ограниченное в точке
имеет ограниченное в точке 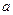 решение
решение 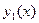 , то все остальные решения
, то все остальные решения  (линейно независимые) не ограничены:
(линейно независимые) не ограничены:  . То есть существует одно ограниченное решение.
. То есть существует одно ограниченное решение.
Доказательство: Из теории ОДУ знаем, что 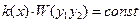 ,
, 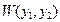 - Вронскиан двух решений. Докажем:
- Вронскиан двух решений. Докажем: 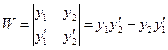 , тогда
, тогда 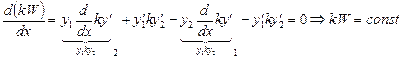 , чтд.
, чтд.
У нас 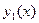 ограничено, а
ограничено, а  - нет. Рассмотрим следующую величину:
- нет. Рассмотрим следующую величину: 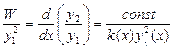 . Проинтегрируем эту величину:
. Проинтегрируем эту величину: 
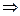
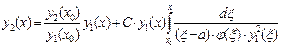 ,
,  , следовательно, этот интеграл расходится при
, следовательно, этот интеграл расходится при 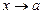 , а это значит, что
, а это значит, что  , чтд.
, чтд.
Уточним теорему: рассмотрим два случая.
1. 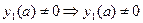 в окрестности точки
в окрестности точки 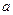 ,
, 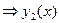 ~
~ 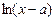 , т.е.
, т.е. 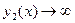 как логарифм.
как логарифм.
2.  ~
~ 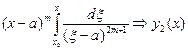 ~
~  - полюс порядка
- полюс порядка 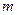 .
.
Проанализируем получившееся решение:
 | Если требуется ограниченное решение в особой точке, то 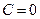 , т.к. , т.к. 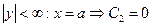 . Так как полное решение (*) всегда является суммой двух решений: ограниченного и неограниченного, то ограниченность этого первого решения уже есть само по себе граничное условие. . Так как полное решение (*) всегда является суммой двух решений: ограниченного и неограниченного, то ограниченность этого первого решения уже есть само по себе граничное условие. |
Уравнение Бесселя.
Рассмотрим уравнение вида:  - уравнение Бесселя. Это уравнение для цилиндрических функций – его решения – цилиндрические функции. Рассмотрим лапласиан в цилиндрических координатах,
- уравнение Бесселя. Это уравнение для цилиндрических функций – его решения – цилиндрические функции. Рассмотрим лапласиан в цилиндрических координатах, 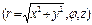 и
и 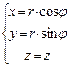 :
: 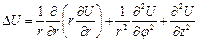 - возникает в связи с решением уравнения Лапласа в цилиндрических координатах.
- возникает в связи с решением уравнения Лапласа в цилиндрических координатах.
Решением этого уравнения (1-ым базисным решнием) является функция Бесселя первого рада:  .
.
Рассмотрим некоторые её свойства.
1) Рекуррентные соотношения. 
2) Функции Бесселя с полуцелыми номерами 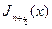 . Вычислим
. Вычислим 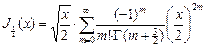 .
.
Для этого выполним преобразования: 
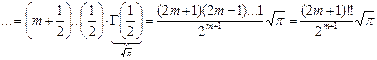 , подставим
, подставим 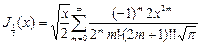 , но
, но  , тогда
, тогда  .
.
Таким образом, мы получили следующие значения: 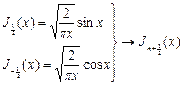 , используя рекуррентные соотношения можно получить остальные значения полуцелых индексов.
, используя рекуррентные соотношения можно получить остальные значения полуцелых индексов.
3) Нули функции Бесселя.
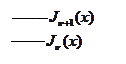  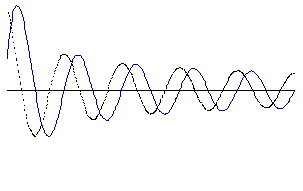 | 1. Они есть и их бесконечно много, следует из асимптотики:  . 2. Все нули, кроме . 2. Все нули, кроме 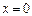 , простые, изолированные. 3. Все нули действительные, положительные. 4. , простые, изолированные. 3. Все нули действительные, положительные. 4. 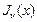 и и  не имеют общих нулей (см. рисунок). 5. При возрастании не имеют общих нулей (см. рисунок). 5. При возрастании 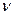 корень смещается, корень смещается, 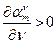 , , 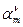 - корни функции Бесселя. - корни функции Бесселя. |
a) особенность, построение ограниченного решения 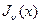 .
.
Будем искать решение уравнения Бесселя в виде ряда Тейлора, умноженного на 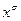 :
: 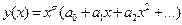 . Подставим это решение в уравнение
. Подставим это решение в уравнение  ,
, 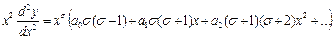 , найдём коэффициенты и выберем ограниченное решение.
, найдём коэффициенты и выберем ограниченное решение.
Подставив решение в уравнение, сравниваем коэффициенты при разных степенях:
При  : :  При При 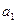 : : 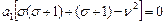 При При 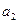 : : 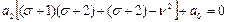 При При 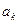 : : 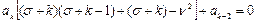 |  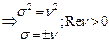 |
Пусть 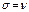 . Таким образом :
. Таким образом :  . Вычислим коэффициент
. Вычислим коэффициент 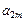 , и выразим его через
, и выразим его через  .
.
 , коэффициент
, коэффициент 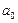 выбираем произвольно:
выбираем произвольно:  , где
, где 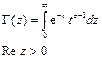 .
.
Таким образом, получили коэффициенты ряда: 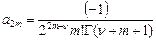 , т.к.
, т.к. 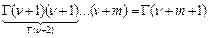 .
.
Запишем формальный ряд: 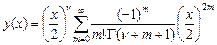 , если
, если 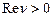 , тогда решение ограничено. Оно решение, т.к. ряд сходится для любых
, тогда решение ограничено. Оно решение, т.к. ряд сходится для любых 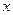 по признаку Даламбера:
по признаку Даламбера:  , сходится при всех
, сходится при всех 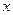 , радиус сходимости равен бесконечности. Таким образом, мы получили единственное, с точность до множителя решение:
, радиус сходимости равен бесконечности. Таким образом, мы получили единственное, с точность до множителя решение:  - функция Бесселя первого рода – это первое базисное решение.
- функция Бесселя первого рода – это первое базисное решение.
Случай 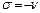 рассмотрен в следующем пункте.
рассмотрен в следующем пункте.
b) общее решение, 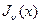 ,
, 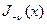 ,
, 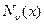 , понятие о функциях
, понятие о функциях 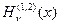 .
.
Будем искать решение уравнения Бесселя в виде ряда Тейлора, умноженного на 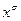 :
: 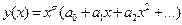 . Подставим это решение в уравнение
. Подставим это решение в уравнение 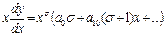 ,
, 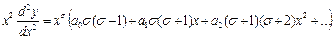 , найдём коэффициенты и выберем ограниченное решение.
, найдём коэффициенты и выберем ограниченное решение.
Подставив решение в уравнение, сравниваем коэффициенты при разных степенях:
При  : :  При При 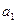 : : 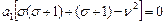 При При 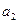 : : 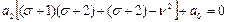 При При 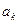 : : 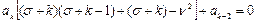 |  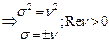 |
Пусть 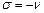 : тогда уравнение решение Бесселя будет:
: тогда уравнение решение Бесселя будет:  , где
, где  - любое нецелое число. Это неограниченное решение значит, оно может выступать в роли второго базисного, но только в случае не целого значения
- любое нецелое число. Это неограниченное решение значит, оно может выступать в роли второго базисного, но только в случае не целого значения 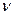 .
.
Пусть 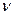 - целое число, тогда
- целое число, тогда  при
при 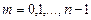 .
. 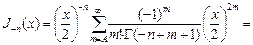 сменим индекс:
сменим индекс: 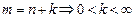
 , получили соотношение:
, получили соотношение: 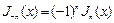 , то есть решения стали линейно зависимыми..
, то есть решения стали линейно зависимыми..
В качестве второго линейно независимого решения уравнения Бесселя можно взять функцию, построенную следующим образом:  - это функция Неймана.
- это функция Неймана.
Её асимптотика 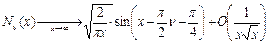 . Оно тоже может играть роль базисного уравнения.
. Оно тоже может играть роль базисного уравнения.
Могут быть и другие линейно-независимые комбинации (базисные решения):
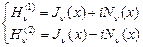 - функции Ханкеля, их асимптотика
- функции Ханкеля, их асимптотика  .
.
Т.о. общее решение уравнения Бесселя имеет вид (линейная комбинация 2-х базисных решений):