Уравнение прямой на плоскости

Прямую l на плоскости можно задать

а) с помощью точки A_oÎ l и ненулевого вектора ½½ l ; тогда можем написать, что

l ={M½ ½½ }; (*)

б) с помощью точки A_oÎ l и ненулевого вектора ^ l ; тогда можем написать, что

l ={M½ ^ }; (**)

в) с помощью двух точек A_o, A₁Î l .

Вектор ½½ l называется направляющим вектором прямой, а вектор ^ l называется вектором нормали к прямой.

Теорема 1. 1. Прямая l, проходящая через точку A_o(x_o, y_o), и имеющая направляющий вектор (a₁, a₂), задается уравнением

= , (9 )

которое называется каноническим уравнением прямой, или параметрическими уравнениями:

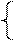x = x_o + a₁t ,

y = y_o + a₂t , tÎR,

которые можно записать в векторном виде так:

= + t, tÎR, (10¢ )

где = – радиус-вектор точки A_o.

2. Прямая, проходящая через две точки A_o(x_o, y_o) и A₁(x₁, y₁), задается уравнением

= , (11 )

3. Прямая, проходящая через точку A_o(x_o, y_o), и имеющая вектор нормали (A, B), задается в декартовой СК уравнением

A(x – x_o) + B(y – y_o) = 0. (12 )

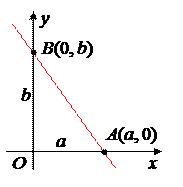4. Прямая, отсекающая на координатных осях отрезки длины a ¹ 0, b ¹ 0, задается уравнением

+ = 1 , (13 )

(уравнение прямой в отрезках).

Предполагается, что в пунктах 1, 2 и 4

СК является произвольной аффинной, а числа a и b в п^o4 могут быть отрицатель-

ными. В уравнениях (10) и (10¢) в дальнейшем писать tÎRне будем: это будет подразумевается.

Доказательство. 1. Пусть M(x, y) – произвольная точка прямой l. Тогда (x – x_o, y – y_o)½½ (a₁, a₂), а по второму признаку коллинеарности векторов (теор.1¢ §7, гл.1) это равносильно (9).

Обратно, если для координат точки M(x, y) выполнено (9), то по тому же признаку ½½ , а значит, MÎ l .

По первому признаку коллинеарности векторов ½½ Û $ tÎR, такое что = t . В координатах последнее равенство имеет вид

x – x_o = t a₁, y – y_o = t a₂,

Для того, чтобы получить уравнение (10) осталось перенести x_o и y_o в другую часть равенства.

2. Если прямая проходит через две точки A_o(x_o, y_o) и A₁(x₁, y₁) , то вектор (x₁– x_o, y₁– y_o) можно взять в качестве направляющего вектора прямой. Подставляя его координаты в (9) вместо a₁, a₂, получим (11).

3. Пусть M(x, y) – произвольная точка прямой l. Тогда

(x – x_o, y – y_o) ^ (A, B) Û · = 0, а в координатах это условие как раз имеет вид (12). Обратно, если координаты точки M(x, y) удовлетворяют (12), то ^ , а значит, MÎ l .

4. Условие означает, что прямая проходит через точки A(a, 0) и B(0, b). Подставляя их координаты в (10), получим

= Û = Û (13) .

При ответе на экзамене недостаточно написать уравнение прямой: требуется обязательно указать, что означает каждый из параметров, входящих в уравнение. Например, выписав каноническое или параметрическое уравнение прямой, следует указать, что (x_o, y_o) – это координаты точки, через которую проходит прямая, а (a₁, a₂) – координаты направляющего вектора. Без данных пояснений ответ в виде выписанного уравнения расценивается, как отсутствие ответа.

Следствие. Любая прямая на плоскости может быть задана уравнением вида

Ax + By + C = 0 , (14)

которое называется общим уравнением прямой. И обратно, любое уравнение вида (14) на плоскости задает прямую.

Доказательство. Любую прямую на плоскости можно задать с помощью точки и вектора нормали. Тогда ее уравнение в декартовой СК будет иметь вид (12). Раскроем скобки:

Ax + By – Ax_o– By_o = 0

и обозначим C = – Ax_o– By_o= const . Получим уравнение (14).

Обратно, пусть некоторое множество l определяется уравнением (14), и A_o(x_o, y_o) – произвольная точка этого множества. Тогда ее координаты удовлетворяют (14): Ax_o + By_o + C = 0 Þ C = – Ax_o– By_o. Подставляя это значение в (14) получим (12), а это уравнение, как уже известно, определяет прямую.

Попутно мы выяснили геометрический смысл коэффициентов A и B в общем уравнении прямой: это координаты вектора нормали к прямой: (A, B). И этот факт чрезвычайно важен при исследовании положения прямой и при решении различных задач про прямую на плоскости. Но этот факт верен только в случае декартовой СК.

Если СК на плоскости не является декартовой, то это следствие можно доказать с помощью уравнения (9). В дальнейшем, СК предполагается декартовой, если не оговорено противное.

Рассмотрим различные частные случаи общего уравнения прямой.

1. C = 0 Û l : Ax + By = 0. Тогда урав-нению удовлетворяют координаты точки O(0, 0), т.е. прямая проходит через начало координат.

2. A = 0 Û By + C = 0 Û y = – C /B. Прямая l||Ox .

3. B = 0 Û Ax + C = 0 Û x = – C /A. Прямая l||Oy .

4. B ¹ 0 . Тогда (14) можно переписать так: y = – x –. Обозначим k = – A/B, q = – C /B, и получим уравнение

y = k x + q, (15)

которое называется уравнением прямой с угловым коэффициентом. Угловым называется коэффициент k. Выясним почему.

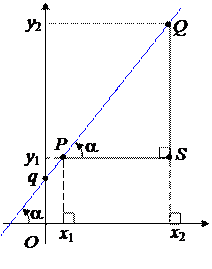
Пусть P(x₁, y₁), Q(x₂, y₂) – две произвольные точки на прямой l, где y₂ ³ y₁. Подставим их координаты в уравнение прямой: y₁ = k x₁ + q, y₂ = k x₂ + q . Вычтем из второго равенства первое:

y₂ – y₁= k (x₂ – x₁).

Поскольку мы исключили случай l½½Oy, то x₂ ¹ x₁ Þ

k = . (*** )

Выберем на прямой l направление, соответствующее возрастанию ординаты y, и назовем его положительным. Пусть a – угол между положительным направлением оси Ox и положительным направлением прямой l. Назовем его углом наклона прямой. Пусть S – точка с координатами (x₂, y₁).

1 случай: x₂ > x₁. Тогда y₂ – y₁ = QS, x₂ – x₁ = PS и из DPQS находим, что k = QS/PS = tg a.

2 случай: x₂< x₁. Тогда y₂ – y₁= QS, x₂ – x₁= – PS Þ k = – QS/PS = = – tg b , где b = ÐQPS. Но b = p – a Þ – tg b = tg a . Значит, как и в первом случае k = QS/PS = tg a.

Итак, мы доказали, что k есть тангенс угла наклона прямой. Поэтому он называется угловым коэффициентом. А геометрический смысл коэффициента q очевиден: это отрезок, отсекаемый прямой на оси Oy.