Метод поиска минимума функции обратным половинным шагом
Применен для указанной функции: y=(x+2)*(x-4)
ВВОД ИСХОДНЫХ ДАННЫХ края диапазона поиска, точность по аргументу ИЛИ по функции
метод обратным половинным шагом
для одномерного поиска экстремума указанной ниже функции
y=(x+2)*(x-4)
исходные данные
введите левую границу интервала поиска -10
введите правую границу интервала поиска 10
ВОПРОС завершение работы по минимальному изменению функции? Да=1 нет=00
введите допустимую погрешность по аргументу:0.1
аргумент:-9.8 функция:107.64
аргумент:-9.6 функция:103.36
аргумент:-9.4 функция:99.16
аргумент:-9.2 функция:95.04
аргумент:-9 функция:91
аргумент:-8.8 функция:87.04
Часть вывода вырезана
аргумент:-0.2 функция:-7.56
аргумент:-2.0539e-015 функция:-8
аргумент:0.2 функция:-8.36
аргумент:0.4 функция:-8.64
аргумент:0.6 функция:-8.84
аргумент:0.8 функция:-8.96
аргумент:1 функция:-9
аргумент:1.2 функция:-8.96
В отличии от приведенного выше примера, работа при достижении минимального изменения функции завершена не была, поэтому произошла смена знака шага по аргументу и его уменьшение вдвое.
dx = -0.1000
аргумент:1.1 функция:-8.99
аргумент:1 функция:-9
xeps
ВОПРОС выводить пошагово как таблицу? Да=1 нет=0 1
ВОПРОС выводить график? Да=1 нет=0 1
вывод результатов
номер= 1 аргумент= -9.800 функция=107.640
номер= 2 аргумент= -9.600 функция=103.360
номер= 3 аргумент= -9.400 функция= 99.160
номер= 4 аргумент= -9.200 функция= 95.040
номер= 5 аргумент= -9.000 функция= 91.000
номер= 6 аргумент= -8.800 функция= 87.040
Часть вывода вырезана
номер= 54 аргумент= 0.800 функция= -8.960
номер= 55 аргумент= 1.000 функция= -9.000
номер= 56 аргумент= 1.200 функция= -8.960
номер= 57 аргумент= 1.100 функция= -8.990
номер= 58 аргумент= 1.000 функция= -9.000
НАЙДЕН МИНИМУМ
оптимальное значение аргумента=1 с точностью (по аргументу):0.1
минимум функции=-9 с точностью (по функции):0.01
выполнено:58 итераций
Метод золотого сечения
В основе этого метода лежит правило геометрического отношения или золотого сечения:
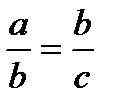или 
,
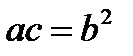где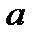 
– длина всего отрезка; 
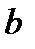– длина его большей части; 
– длина его меньшей части.
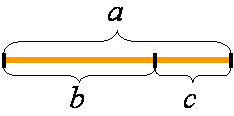
Рис. 2.5. Графическая иллюстрация правила золотого сечения
В соответствии с этим правилом определяются точки исследуемого интервала, в которых необходимо производить вычисление функции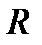 
.
Из рис. 2.5 следует, что:
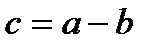. (1)
Тогда, подставляя в (1) соотношение (2) получим:
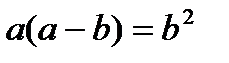. (2)
Обозначив отношение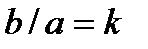 
и подставив его в (2), получим:
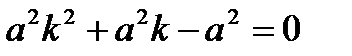, (3)
откуда следует:
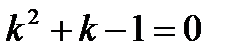. (4)
Решение этого уравнения дает:
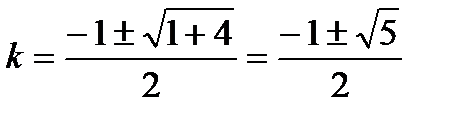. (5)
Поскольку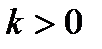 
, то его значение принимается равным:
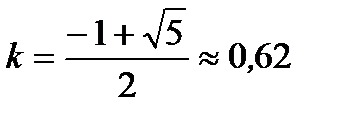. (6)
| R |
| х3 |
| х1 |
| х2 |
| х4 |
| хmin |
| хmax |
Рис. 2.6. Графическая иллюстрация метода золотого сечения
На исследуемом интервале (рис. 2.6) определяются две точки X1 = Xmin + k²a и X2 = Xmin + ka, где а – длина интервала [Xmin, Xmax]. Находим значения функции в точках Xmin, X1, X2, Xmax. Если наименьшее значение R будет соответствовать точке X1, то новым интервалом поиска будет [Xmin, X2], и на этом интервале находится новая точка X3 = Xmin + k²a, где ka – длина интервала [Xmin, X2] Если наименьшее значение R будет в соответствовать точке X2, то новым интервалом поиска будет [X1, Xmax], и на этом интервале находится новая точка X4 = X1 + ka, где ka – длина интервала [X1, Xmax]. Затем процедура повторяется. Абсолютная ошибка в определении экстремума после s вычислений будет вычисляться по формуле:
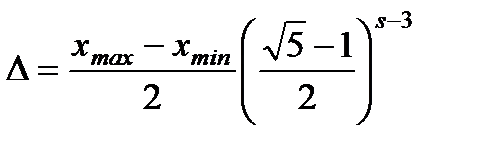. (7)
Далее приведен текст программы, позволяющий реализовать описанный выше алгоритм.
function[]=ZolotSechenie1D_170809();
function y=f(x)
y=(x+2).*(x-4);
end
disp('МЕТОД ПОИСКА МИНИМУМА ФУНКЦИИ МЕТОДОМ ЗОЛОТОГО СЕЧЕНИЯ');
disp('Применен для указанной функции: y=(x+2)*(x-4)');
disp('ВВОД ИСХОДНЫХ ДАННЫХ точность по аргументу, края диапазона поиска');
function [x,y,xleft1,xright1,nn]=ZolS1()
eps=input('точность=');
xleft=input('левый край поиска=');
xright=input('правый край поиска=');
xleft1=xleft; %возвращаемые значения
xright1=xright; %возвращаемые значения
k=(sqrt(5)-1)/2; %число К, показывающее отношения длин отрезков
x1=xleft+k*k*abs(xleft-xright);
x2=xleft+k*abs(xleft-xright);
z=0;
j=0;
nn=1;
disp('ВЫВОД ПРОМЕЖУТОЧНЫХ РЕЗУЛЬТАТОВ ПОШАГОВО ');
while abs(xleft-xright)>eps
R1=f(x1);
R2=f(x2);
if R1<R2 % если минимум в точке Х1
z=x1; % для возвращения значения минимума
j=R1; % для возвращения значения минимума
%для следующей итерации подготавливаем интервал с четырьмя точками по правилу золотого сечения вместо xleft,x1,x2
xright=x2;
x2=x1;
x1=xleft+k*k*abs(xleft-xright);
%возвращаемые значения
mas1x(nn)=x1;
mas1y(nn)=R1;
else %если минимум в точке Х2
z=x2;
j=R2;
%для следующей итерации подготавливаем интервал с четырьмя точками по правилу золотого сечения вместо x1,x2,xright
xleft=x1;
x1=x2;
x2=xleft+k*abs(xleft-xright);
%возвращаемые значения
mas1x(nn)=x2;
mas1y(nn)=R2;
end %конец if
%вывод на экран минимума функции и соответствующего аргумента соответствующего аргумента для выполнения итерации
string=strcat('шаг номер:',int2str(nn),' аргумент:',num2str(mas1x(nn)),' функция от него:',num2str(mas1y(nn)));
disp(string);
nn=nn+1;
end %конец while
%возвращаемые значения найденного минимума и возвращения значения
x=z;
y=j;
nn=nn-1;
end
%обращение к функции методом золотого сечения
[x,y,xleft1,xright1,nn]=ZolS1();
%выбор оформления вывода на экран
choiceTab=input('ВОПРОС выводить пошагово как таблицу? Да=1 нет=0 ');
choiceGraf=input('ВОПРОС выводить график? Да=1 нет=0 ');
%вывод таблицы
if choiceTab==1
disp('вывод результатов');
for i=1:nn
string=print(‘номер= %4i\tаргумент= %7.3f\tфункция= %7.3f’,i,mas1x(i),mas1y(i));
disp(string);
end
end
disp('НАЙДЕН МИНИМУМ')
sx=strcat('оптимальное значение аргумента=',num2str(x),' с точностью:',num2str(abs(mas1x(nn)-mas1x(nn-1))));
sy=strcat('минимум функции=',num2str(y),' с точностью:',num2str(abs(mas1y(nn)-mas1y(nn-1))));
sn=strcat('выполнено:',num2str(nn),' итераций');
disp(sx) % вывод на экран
disp(sy)
disp(sn)
% подготовка к построению графика
h=0.1;
x1=xleft1:h:xright1;
y1=f(x1);
plot(x1,y1,'k-');
grid on;
title('y=(x+2)(x-4)');
xlabel('X'); ylabel('Y');
text(x,y,’\leftarrow Minimum’);
zeroMas=x1*0;
hold on;
if choiceGraf==1
plot(mas1x,mas1y,’r.’);
legend(‘plot with minimal step’,’points by Gold method’,0);
else
legend(‘plot with minimal step’,0);
end
hold on;
plot(x1,zeroMas,’k-‘,zeroMas,y1,’k-‘);
end
После выполнения этой программы пользователь видит на экране соответствующий текст, вводит нужные значения и получает график:
МЕТОД ПОИСКА МИНИМУМА ФУНКЦИИ МЕТОДОМ ЗОЛОТОГО СЕЧЕНИЯ
Применен для указанной функции: y=(x+2)*(x-4)
ВВОД ИСХОДНЫХ ДАННЫХ точность по аргументу, края диапазона поиска
точность=0.1
левый край поиска=-10
правый край поиска=10
ВЫВОД ПРОМЕЖУТОЧНЫХ РЕЗУЛЬТАТОВ ПОШАГОВО
шаг номер:1 аргумент:5.2786 функция от него:-7.1486
шаг номер:2 аргумент:0.55728 функция от него:-7.1486
шаг номер:3 аргумент:-0.55728 функция от него:-8.804
шаг номер:4 аргумент:1.2461 функция от него:-8.804
Часть вывода вырезана
шаг номер:9 аргумент:0.92089 функция от него:-8.9997
шаг номер:10 аргумент:1.0214 функция от него:-8.9997
шаг номер:11 аргумент:0.95928 функция от него:-8.9997
шаг номер:12 аргумент:0.99767 функция от него:-8.9997
ВОПРОС выводить пошагово как таблицу? Да=1 нет=0 1
ВОПРОС выводить график? Да=1 нет=0 1
вывод результатов
номер= 1 аргумент= 5.279 функция= -7.149
номер= 2 аргумент= 0.557 функция= -7.149
номер= 3 аргумент= -0.557 функция= -8.804
номер= 4 аргумент= 1.246 функция= -8.804
номер= 5 аргумент= 1.672 функция= -8.939
номер= 6 аргумент= 0.983 функция= -8.939
номер= 7 аргумент= 0.820 функция= -9.000
номер= 8 аргумент= 1.084 функция= -9.000
номер= 9 аргумент= 0.921 функция= -9.000
номер= 10 аргумент= 1.021 функция= -9.000
номер= 11 аргумент= 0.959 функция= -9.000
номер= 12 аргумент= 0.998 функция= -9.000
НАЙДЕН МИНИМУМ
оптимальное значение аргумента=0.98301 с точностью:0.038388
минимум функции=-8.9997 с точностью:0
выполнено:12 итераций
Рис. 2.7. Пример применения метода золотого сечения