Выпуклость и вогнутость графика функции. Точки перегиба

Для уточнения поведения функции и формы графика функции рассмотрим вопросы, связанные с понятием направления выпуклости.

Определение.

График дифференцируемой функции 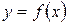называется выпуклым (вогнутым) на интервале 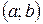, если он расположен ниже (выше) любой касательной, проведенной к данному графику (рис.5.8).

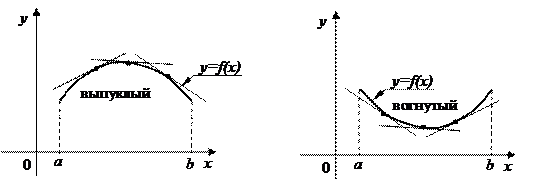Рис. 5.8

График функции в одних интервалах может быть выпуклым, а в других − вогнутым. Интервалы выпуклости и вогнутости находят с помощью следующей теоремы.

Теорема.

Если функция 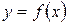во всех точках интервала 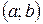имеет отрицательную вторую производную: 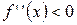, то график функции в этом интервале выпуклый. Если 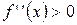− график вогнутый.

Определение.

Точка графика непрерывной функции 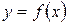, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба (рис.5.9).

Рис. 5.9

Из определения следует, что при переходе через точку перегиба, меняется направление выпуклости кривой, следовательно, 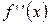в этой точке меняет свой знак. Заметим, что 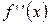может менять свой знак лишь в точках, где она равна нулю, или в точках, где 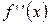не существует. Отсюда получаем необходимое и достаточное условия точки перегиба.

Теорема(необходимое условие существования точки перегиба)

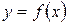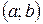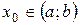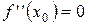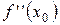Если функция дважды дифференцируема на интервале и является точкой перегиба, то или не существует.

Теорема(достаточное условие существования точки перегиба)

Если вторая производная 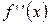при переходе через точку 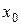, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой 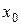есть точка перегиба.

Для отыскания интервалов выпуклости и вогнутости и точек перегиба графика функции используют следующую схему:

1) найти ;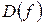

2) найт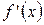и и ;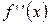

3) определить точки, в которых 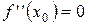или не существует (в частности, );

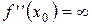4) исследовать знак 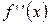слева и справа от каждой такой точки;

5) указать координаты точек перегиба и интервалы выпуклости и вогнутости.

Пример

Найти интервалы выпуклости и вогнутости и точки перегиба графика функции .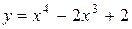

1) ;

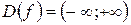2) , ;

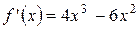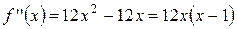3) , , , ;

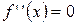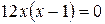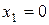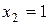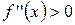для ; (« »);

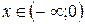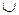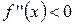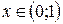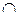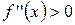для ; (« »);

для ; (« »);.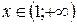

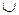4) , .

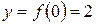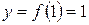Точки перегиба имеют координаты 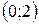и .

И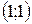нтервалы выпуклости: .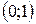

Интервалы вогнутост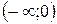и: и .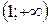

Асимптоты графика функции

Построение графика функции значительно облегчается, если знать его асимптоты.

Определение.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).

Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.

Рис. 5.10

Вертикальные асимптоты

Определение.

Прямая 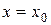называется вертикальной асимптотой графика функции 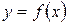, если выполнено одно из условий:

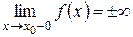или 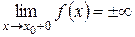(рис.5.11)

Рис. 5.11

Вертикальные асимптоты, уравнение которых х=x₀ , следует искать в точках, где функция терпит разрыв второго рода, или на концах ее области определения, если концы не равны 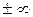. Если таких точек нет, то нет и вертикальных асимптот.

Например, для кривой 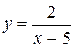, вертикальной асимптотой будет прямая 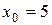, так как 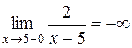, 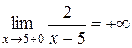. Вертикальной асимптотой графика функции 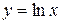является прямая 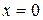(ось Оу), поскольку

.
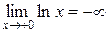