Основные типы расчетов на прочность

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Методические указания для самостоятельной

работы студентов

Красноярск 2011

ОГЛАВЛЕНИЕ

Введение 4

1. Растяжение-сжатие 5

Задача 1. Расчёт статически определимой стержневой

системы при растяжение (сжатие) 8

Задача 2. Расчёт статически определимого ступенчатого

бруса при растяжение (сжатие) 16

Задача 3. Расчёт статически неопределимого

ступенчатого бруса при растяжение (сжатие) 23

Плоский изгиб 30

Задача 4. Плоский изгиб балки 32

Кручение вала 39

Задача 5. Кручение вала 40

Рекомендуемая литература 46

Введение

Современная действительность требует ускорения научно-технического прогресса, повышения конкурентоспособности выпускаемой продукции, снижения материалоемкости конструкции, повышения производительности, долговечности, надежности машин. Исключительная роль в обеспечении этого процесса принадлежит инженерам, конструкторам, машиностроителям. Значительная роль в формировании облика инженеров широкого профиля отводится дисциплинам общеинженерного цикла и, в частности, дисциплине «Сопротивление материалов». Создавая новую конструкцию, инженер назначает первоначальные размеры ее элементов, проводя прочностные расчеты методами сопротивления материалов. Дальнейший расчет конструкций, как правило, производится с помощью ЭВМ численными методами с использованием пакетов прикладных программ. Однако для анализа достоверности получаемых результатов используется сравнение с результатами расчетов по упрощенным моделям методами сопротивления материалов.

В решении задачи по ускорению развития агропромышленного комплекса страны важная роль принадлежит науке о прочности материалов и конструкций, назначение которой – повысить качество расчета и проектирования, дать теоретическую основу для разработки новых эффективных материалов и конструкций и тем самым способствовать повышению эффективности качества, надежности и экономичности сооружений конструкций машин и приборов.

Цель курса «Сопротивление материалов» - выработка у студента умения производить расчеты на прочность, жесткость и устойчивость элементов инженерных конструкций, применяемых в агропромышленном комплексе, подготовить его к правильному выбору методов расчета и проектирования, с целью обеспечения надежности, экономичности и снижения материалоемкости этих конструкций.

У студентов, изучающих курс «Сопротивление материалов», наибольшие трудности обычно возникают при решении задач. Настоящее методическое указание призвано облегчить процесс изучения данного курса, а главное помочь овладеть методикой решения задач и получить необходимый навык в их решении.

Методическое указание содержит материал, относящийся к разделам: растяжение-сжатие, плоский поперечный изгиб, кручение вала.

В данное методическое указание включены задания для самостоятельной работы студента (30 вариантов задач на каждую тему) и примеры решения типовых задач.

Номер схемы определяется по сумме двух последних цифр шифра зачётной книжки, а номер варианта – по последней цифре шифра.

Растяжение-сжатие

Осевым растяжением бруса называется вид нагружения, при котором равнодействующая внешних сил прикладывается в центре тяжести поперечного сечения и действует вдоль продольной оси. В этом случае в поперечных сечениях стержня из шести внутренних силовых факторов возникает только один – продольная осевая сила N.

Для определения внутренних усилий используется метод сечений.

Сущность метода заключается в следующем:

1. Рассекают (мысленно) тело на две части плоскостью, перпендикулярной продольной оси тела (поперечным сечением).

2.Отбрасывают правую или левую часть тела. Чтобы оставшаяся часть находилась в равновесии, по плоскости сечения должны действовать внутренние силы.

3.Заменяют действие одной части на другую внутренними силами. Так как отсеченная часть тела находится в равновесии, то для определения внутренних усилий, в общем случае нагружения, составляют шесть уравнений статического равновесия:

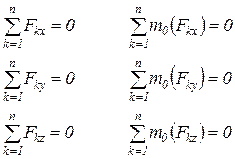
При растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N.

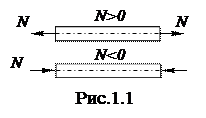Нормальная сила считается положительной, если она растягивает отсеченную часть стержня, (направлена по внешней нормали), при сжимающем действии нормальная сила считается отрицательной, что можно изобразить графически, как показано на рис.1.1.

Нормальная сила в сечении бруса является равнодействующей нормальных напряжений, действующих в плоскости поперечного сечения

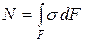
Закон распределения напряжений может быть определен из эксперимента. Установлено, что если на стержень нанести прямоугольную сетку, то после приложения продольной нагрузки вид сетки не изменится, она по-прежнему останется прямоугольной, а все линии прямыми. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций, а на основании закона Гука ( 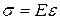) и нормальных напряжений s = const. Тогда N = s F , откуда получим формулу для определения нормальных напряжений в поперечном сечении при растяжении .

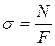Подставляя напряжение в закон Гука получим:

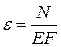
От сюда .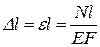

Эта формула выражает закон Гука для абсолютных удлинений. Произведение EF называется жёсткостью поперечного сечения при растяжении и сжатии.

Полное удлинение участка длиной l получим, суммируя удлинения всех бесконечно малых участков.

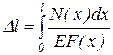
Основные типы расчетов на прочность

Используя условие прочности, можно решать следующие основные типы расчетов:

Проектировочный расчет - определение по известной нагрузке и допускаемому напряжению размеров поперечного сечения стержня .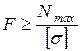

Проверочный расчет - проверка прочности стержня, т.е. определение по заданным нагрузке и размерам поперечного сечения стержня фактических напряжений и сравнение их с допускаемыми .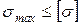

Определение максимальной нагрузки по заданным размерам поперечного сечения и [s]

.

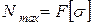Определив допускаемую нормальную силу N_max и установив связь между нормальной силой и нагрузкой с помощью метода сечений, можно определить и максимальную нагрузку P_max.