Исследование функций на монотонность и экстремумы

Производная помогает также при исследовании функции на возрастание и убывание. Напомним вначале соответствующее определение.

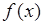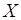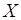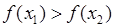
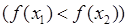
Определение. Пусть функция определена на промежутке . Говорят, что она возрастает (убывает) на промежутке , если 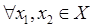таких, что .

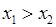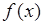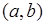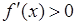
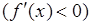
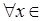
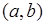Теорема. Если функция дифференцируема на интервале и , то 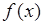возрастает (убывает) на интервале .

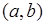Пусть производная функции 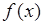непрерывна на промежутке 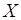. Для исследования ее на возрастание и убывание обычно придерживаются следующего плана:

1) Найти точки из 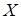, где 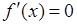. Эти точки называются стационарными.

2) Во всех промежутках, на которые разбивают 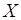стационарные точки, определить знак 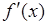. Для этого достаточно определить знак 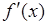в одной точке каждого промежутка (знак внутри каждого промежутка не меняется, поскольку в противном случае внутри этого промежутка по теореме Больцано-Коши должен быть нуль производной, что невозможно). Если внутри промежутка 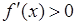, то здесь 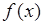согласно теореме возрастает. Если 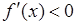, то убывает.

Определение. Точки, в которых производная функции равна нулю, называются стационарными. Точки, в которых производная функции равна нулю или не существует, называются критическими.

Пример. Исследовать на возрастание и убывание функцию

.

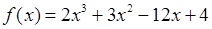Данная функция дифференцируема на всей числовой прямой.

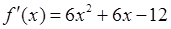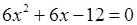
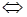
1) . Найдем стационарные точки: 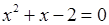. Корнями уравнения являются числа , .

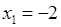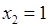2) Точки 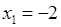, 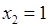разбивают числовую прямую на три интервала: , , .

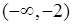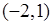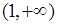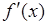+ - + На первом интервале возьмем .

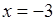-2 1 ;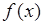

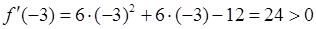Следовательно, на промежутке 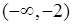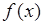возрастает. На промежутке 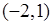возьмем 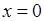, 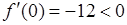. Поэтому 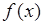убывает. На интервале 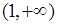возьмем 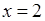, 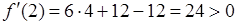. Поэтому на интервале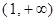 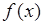возрастает.

Определение.Пусть функция 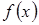определена в 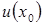. Точка 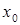называется точкой локального максимума (минимума), если cуществует 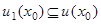такая, что

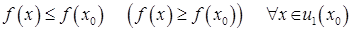. (1)

Если неравенства (1) строгие при 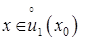, то точка 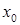называется точкой строгого локального максимума (минимума). Точки локального максимума и минимума называются точками экстремума.

Теорема(необходимое условие экстремума). Если функция 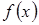дифференцируема в точке 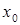и 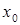является точкой экстремума, то

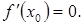(2)

Доказательство теоремы не сложно получить из определения производной.

Замечание.Из теоремы следует, что точки экстремума функции 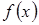нужно искать среди стационарных точек и точек, где производная не существует. Одно из достаточных условий экстремума непосредственно вытекает из следующей теоремы.

Замечание.Необходимое условие не является достаточным. Например, для функции 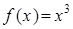имеем 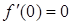, но точка 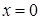не является экстремумом, поскольку функция 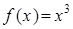возрастает на всей числовой прямой.

Теорема (достаточное условие экстремума). Пусть функция 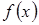непрерывна в точке 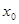и дифференцируема в 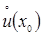. Тогда:

а) если производная 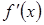при переходе через точку 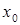меняет знак с плюса на минус, то точка 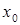является точкой локального максимума;

б) если производная 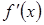при переходе через точку 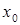меняет знак с минуса на плюс, то точка 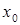является точкой локального минимума функции .

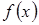Заметим, что из теоремы следует, что в предыдущем примере точка 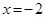является точкой локального максимума, а точка является точкой локального минимума функции .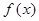

Часто при решении различных задач приходится находить наибольшее и наименьшее значения функции на некотором множестве .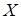

Рассмотрим как решается эта задача сначала для случая, когда 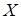это отрезок 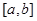. Пусть функция 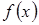непрерывна на отрезке 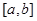и дифферецируема на интервале 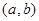за исключением, быть может, конечного числа точек. Тогда, согласно теореме Вейерштрасса функция 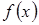достигает на отрезке 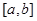наибольшее и наименьшее значения.

Из приведенных теорем вытекает следующий план отыскания наибольшего и наименьшего значений функции .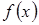

1) Найти производную 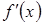и нули производной из .

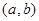2) Найти значения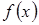

а) в нулях производной из ;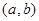

б) на концах отрезка ;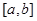

в) в точках, где производная не существует.

3) Из полученных чисел выбрать наибольшее и наименьшее.

Замечание 1.Заметим, что находить промежутки возрастания и убывания здесь совсем не обязательно.

Замечание 2.Если 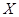является интервалом, полуинтервалом или бесконечным промежутком, то выше приведенным планом пользоваться нельзя. В этом случае для решения задачи о наибольшем и наименьшем значении нужно найти промежутки возрастания и убывания функции, пределы в граничных точках и с помощью не сложного анализа получить ответ.

Пример 3. Найти наибольшее и наименьшее значения функции 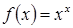на промежутке .

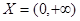Найдем промежутки возрастания и убывания. Для этого найдем производную:

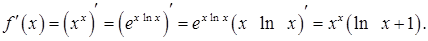
Далее действуем по плану. Найдем нули производной:

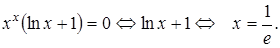
Точка 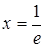разбивает промежуток 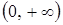на два интервала: 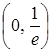и 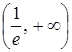. Найдем в этих интервалах знак производной. Для этого вычислим

,

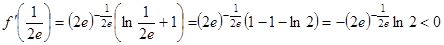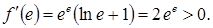
Таким образом, на полуинтервале 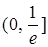функция убывает, а на промежутке 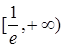возрастает. Поэтому 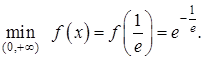Наибольшего значения не существует, так как 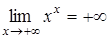. В этом случае пишут: .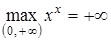