Системы линейных алгебраических уравнений

Матрицы

Матрицей называется прямоугольная таблица чисел размерности m´n.Она кратко записывается в виде А=(а_ij), .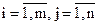

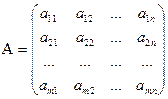
Числа (а_ij) 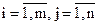-элементы матрицы; i-номер строки; j-номер столбца.

Две матрицы А=(а_ij), В=(b_ij), одинаковой размерности m´n называются равными, если а_ij= b_ij, .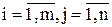

Суммой матриц А=(а_ij), В=(b_ij) одинаковой размерности m´n называется матрица С=( а_ij + b_ij), .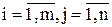

Сложение матриц подчиняется законам коммутативности и ассоциативности и сочетательным законам: А + В = В + А, (А + В) + С = А + (В + С).

Матрица, все элементы которой нули, называется нулевой матрицей, обозначается 0. А + 0 =А.

Произведением матрицы А на число m называется матрица В=mА=(m а_ij), .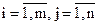

Произведением матрицы А=(а_ij) размерности m´p на матрицу В=(b_ij) размерности p´n (число столбцов матрицы А должно быть равно числу строк матрицы В) называется матрица С=(a_i1b_1j+ ai₂b_2j + ...+ a_ipb_pj), .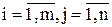

Произведение матриц в общем случае не подчиняется коммутативному закону: АВ¹ВА.

Для более простого запоминания и понимания правила умножения матриц возможно его восприятия следующим образом: при умножении строка первой матрицы накладывается на столбец второй, все числа наложенные друг на друга перемножаются, а результаты этих произведений складываются между собой.

Таким образом для получения элемента c_ij результирующей матрицы С необходимо i-тую строку матрицы А наложить на j-тый столбец матрицы В.

Для матриц остаются справедливы следующие соотношения:

А(ВС)=(АВ)С, (А + В)С = АС + ВС.

Особый класс среди матриц представляют собой, так называемые квадратные матрицы.

Квадратной матрицей n-ого порядка называется таблица чисел.

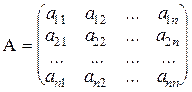
Одной из характеристик квадратной матрицы служит ее определитель (детерминант).

Определителем (детерминантом) II порядка, соответствующим квадратной матрице II порядка, называется число, обозначаемое символом:

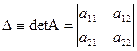и вычисляемое по правилу: произведение элементов лежащих на главной диагонали минус произведение элементов лежащих на дополнительной диагонали D=a₁₁ a₂₂ - a₂₁ a₁₂.

Определителем III порядка, соответствующим квадратной матрице III порядка, называется число, вычисляемое по правилу: произведение элементов лежащих на главной диагонали плюс произведение элементов лежащих в углах треугольника с основанием параллельным главной диагонали минус произведение элементов лежащих на дополнительной диагонали и минус произведение элементов лежащих в углах треугольника с основанием параллельным дополнительной диагонали

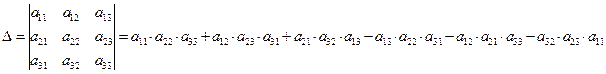
К сожалению, для матриц более высокого порядка таких простых правил вычисления определителя не существует.

Минором М_ij элемента а_ij определителя называется определитель, полученный из данного путем вычеркивания i-ой строки и j-го столбца.

Алгебраическим дополнением А_ij элемента а_ij называется число А^(ij)=(-1)^i+j М_ij

Определителем (детерминантом) матрицы n-ого порядка является число вычисляемое при помощи следующей формулы: 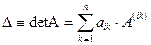. Применение данной формулы при вычислении определителей называют разложением определителя по строке.

Для определителя справедливо выполнение следующих свойств:

1. Определитель равен нулю, если: все элементы какой-нибудь строки равны нулю или соответствующие элементы двух строк пропорциональны.

2. Определитель матрицы равен определителю транспонированной матрицы (матрица транспонируется если в ней поменять местами строки и столбцы)

3. При перестановке двух строк в квадратной матрице определитель меняет знак.

4. Общий множитель всех элементов строки можно вынести за знак определителя.

5. Определитель не изменится, если к одной его строке прибавить другую строку, умноженную на одно число не равное нулю.

На использовании вышеперечисленных свойств основан метод Гаусса вычисления определителя матрицы. Метод Гаусса заключается в том, чтобы используя свойства 3-5 получить из исходной матрицы матрицу треугольную, т.е. такую у которой ниже диагонали нули. Определитель треугольной матрицы равен произведению диагональных элементов (Это не сложно показать, раскладывая определитель каждый раз по последней строке).

Для квадратных матриц одинакового порядка умножение всегда возможно. Особое значение при таком умножении имеет так называемая единичная матрица Е, у которой по главной диагонали стоят единицы, а выше и ниже диагонали - нули:

Очевидно, что определитель единичной матрицы detE=1. Легко проверяется, что АЕ=ЕА=А.

Если матрица С=АВ для квадратных матриц А и В, то detC=detA^.detB. Для квадратной матрицы вводится понятие обратной матрицы.

Матрица А^-1 называется обратной для квадратной матрицы А, если:

АА^-1=А^-1А=Е

Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. detA=D¹0

Нахождение обратной матрицы возможно двумя способами.

1. Способ присоединенной матрицы: по формуле ,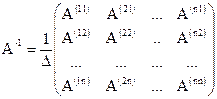

где А^(ij), 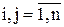-алгебраические дополнения элементов a_ij определителя

D=detA= .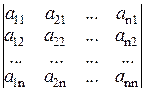

2. Нахождения обратной матрицы методом элементарных преобразований:

Элементарными преобразованиями являются:

а) перестановка двух строк в матрице.

б) умножение или деление всех элементов строки на одно и тоже число .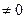

в) вычитание из одной строки матрицы другой строки умноженной на число .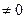

Записав рядом с исходной квадратной матрицей, через черту, единичную квадратную матрицу того же порядка, и применяя к вновь построенной матрице элементарные преобразования таким образом чтобы на месте исходной матрицы получилась единичная, получим на месте единичной матрицы матрицу обратную к исходной.

Вектора.

Вектором называется направленный отрезок, т.е. отрезок прямой, характеризующийся длиной и направлением: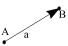

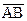Из двух граничных точек этого отрезка одна является началом, а другая концом. Вектор обозначается или , где А - начало, В - конец вектора; длина вектора (модуль) обозначается символом |а| или | |.

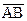Нуль - вектором называют вектор, конец которого совпадает с началом.

Два вектора называются коллинеарными, если они расположены на параллельных прямых.

Три вектора называются компланарными, если они расположены в параллельных плоскостях.

Равными считаются векторы, которые : коллинеарны, сонаправлены и имеют равные модули.

Суммой + векторов и при условии, что конец вектора совмещен с началом вектора , называется вектор 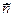соединяющий начало вектора сконцом вектора .

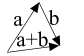
Сложение векторов коммутативно и ассоциативно:

+ = + ( + )+ = +( + )

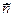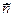Разностью - векторов и называется вектор 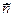для которого + =

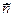Произведением l вектора на число l называется вектор ` такой,что |` | = |l| | |; ` коллинеарен вектору и направлен в ту же сторону при l>0 и в противоположную сторону - при l<0.

При умножении вектора на число выполняются следующие соотношения:

(lm) =l(m ) l( + )=l +l

Линейной комбинацией векторов 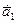, ,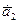…, 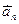называется вектор

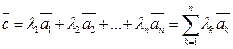
где 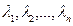-произвольные действительные числа.

Вектора 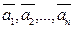линейно зависимы, если $ 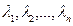одновременно не равные нулю такие что линейная комбинация равна нулю, в противном случае вектора 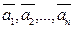линейно-независимы

Два коллинеарных вектора всегда линейно-зависимы, а два неколлинеарных вектора линейно независимы.

Три компланарных вектора линейно-зависимы, а три некомпланарных – линейно-независимы.

Любые четыре вектора в пространстве линейно-зависимы.

Базисом называется максимальная линейно-независимая система векторов (добавление к системе еще одного вектора делает ее линейно зависимой )

Базисом на плоскости являются любые два неколлинеарных вектора, взятых в определенном порядке, а базисом в пространстве - любые три некомпланарных вектора, взятых в определенном порядке.

Любой вектор представим как линейная комбинация базисных векторов.

Коэффициенты разложения вектора по базисным векторам называются координатами вектора в базисе ` : ={ }.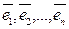

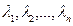При сложении или вычитании векторов складываются или вычитаются их соответствующие координаты.

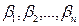={ }, ={ }, Þ 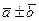={a₁ ± b₁, a₂ ± b₂,…, a_n ± b_n} ;

При умножении вектора на число l все его координаты умножаются на это число.

Отметим, что если векторы и коллинеарны, то их координаты пропорциональны.

По аналогии с множеством векторов на плоскости и в пространстве можно ввести понятие n – мерного вектора в n – мерном пространстве.

Множество всех n - мерных векторов = (a₁, a₂,...,a_n), a_iÎR, для которых определены операции сложения и умножения на число, называется арифметическим n- мерным векторным пространством Rⁿ

В частности, R² - множество векторов на плоскости,R³ - множество векторов в пространстве.

Для пространства Rⁿ сохраняются определения линейной комбинации и линейной зависимости векторов ` .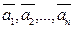

Базисом в Rⁿ называется любая система n линейно независимых векторов, число n называется размерностью пространства Rⁿ.

Прямоугольной декартовой системой координат (ПСК) называется совокупность точки О и ортонормированного базиса `i,`j,`k, т.е. такого базиса, в котором векторы единичны (имеют длины, равные 1) и взаимно перпендикулярны. Три взаимно перпендикулярные прямые в направлении базисных векторов называются осями координат: оси абсцисс, ординат, аппликат.

Обычно рассматривается правая система координат, т.е. такая, что из конца вектора `к кратчайший поворот от`i к`j виден против часовой стрелки.

Точке М в пространстве соответствует радиус-вектор 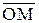. Координатами точки М назовем координаты вектора 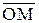: 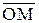=x_M`i +y<sub>M</sub> `j +z_M`k , т.е. М(х_М,y_M,z_M).

Длина 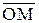- диагональ прямоугольного параллепипеда вычисляется как 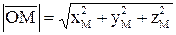. Если вектор `a расположен в пространстве произвольно, то `a=a_x`i+a<sub>y</s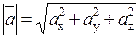ub>`j +a_z`k, . Пусть А(х_А,y_A,z_A)-его начало, B(x_B,y_B,z_B)-его конец, тогда =ОВ–ОА={x_B-x_A, y_B-y_A, z_B-z_A}, .

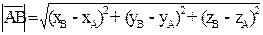Направляющими косинусами вектора называются косинусы углов, образуемых им с координатными осями.

Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла между ними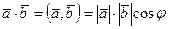

Для скалярного произведения справедливо:

1.

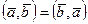
2.

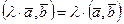
3.

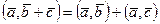
Из этих свойств следует, что при скалярном умножении можно раскрывать скобки так же, как при умножении многочленов.

Через координаты скалярное произведение представляется следующим образом: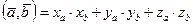

Необходимым и достаточным условием перпендикулярности ненулевых векторов и является равенство нулю их скалярного произведения.

Кроме того используя скалярное произведение становиться возможным находить угол между векторами 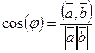где φ угол между векторами и .

Векторным произведением векторов и называется вектор 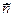, определяемый следующим образом:

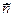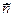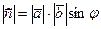^ , ^ ; ; вектора , и 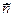образуют правую тройку

Векторное произведение обозначается символами = ´ =[ , ]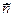

Для векторного произведения справедливо:

1.

2.

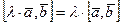
3.

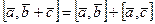
Через координаты векторное произведение представляется следующим образом: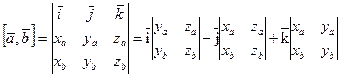

Необходимым и достаточным условием коллинеарности ненулевых векторов и является равенство нулю их векторного произведения.

Кроме того используя векторное произведение становиться возможным находить площадь параллелограмма и площадь треугольника построенного на этих векторах: S_□= ;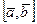

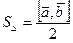
Смешанным (векторно-скалярным) произведением трех векторов , и 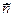называется число равное ( , , )=([ , ], )

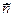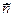Смешанное произведение ( , , 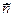) с точностью до знака равно объему параллелепипеда, построенного на векторах , , 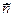. Произведение имеет знак (+), если тройка , , 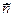- правая, (-) - если тройка , , 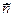- левая.

Необходимым и достаточным условием компланарности трех ненулевых векторов , , 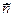является равенство нулю их смешанного произведения.

Через координаты смешанное произведение представляется следующим образом: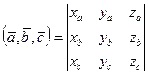

Системы линейных алгебраических уравнений.

Системой m линейных алгебраических уравнений (СЛАУ) с n неизвестными будем называть следующую систему:

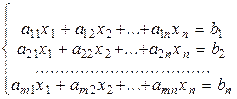
где x_j, j= 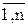-неизвестные; а_ij, 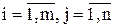-коэффициенты при неизвестных; b_i, 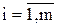- свободные члены. При b_i=0, 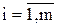, система называется однородной.

Решением системы называется такая совокупность чисел 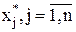, которая при подстановке 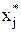вместо 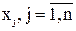в каждое уравнение системы обращает его в тождество.

СЛАУ называется совместной, если она имеет решение, несовместной - если решения нет

Однородная система всегда совместна, т.к. имеет нулевое решение.

Совместная система называется определенной, если она имеет единственное решение, неопределенной - если решений бесконечное множество.

Две совместные системы называются равносильными, если все их решения совпадают.

Коэффициенты при неизвестных в системе составляют прямоугольную таблицу - матрицу A_mn из m строк и n столбцов, она называется основной матрицей системы, а матрица (А\В) - расширенной:

.

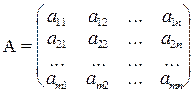
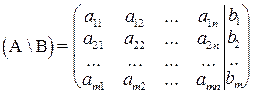Строки и столбцы матрицы можно воспринимать как вектора.

Рангом матрицы А (обозначается rgA) называется максимальное число линейно-независимых строк матрицы.

Теорема Крониккера-Капелли. Система линейных уравнений совместна тогда, когда rang(A)=rang(A\B).

В случае если матрица системы представляет из себя, не вырожденную квадратную матрицу, то возможны три метода ее решения.

Матричный метод.

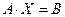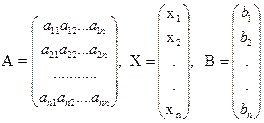
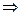
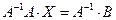
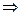
Исходную систему уравнений можно представить в виде , где 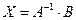. Таким образом, вектор столбец переменных представляет из себя произведение обратной матрицы к матрице системы на вектор столбец свободных членов.

Метод Крамера.

Неизвестные системы определяют по формулам: 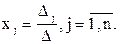Где D - определитель исходной матрицы системы, а D_j определитель получается из определителя D заменой j-го столбца столбцом свободных членов.

Метод Гаусса.

Данный метод заключается в последовательном исключении неизвестных из уравнений системы путем элементарных преобразований над расширенной матрицей.

Процесс продолжаем, пока не получим треугольную матрицу.

Из последней строки определим x_n, зная значение этой переменной из предпоследней строки определим значение x_n-1, …

Данный метод легко обобщаем на случай когда число переменных не равно числу уравнений.

Также при помощи элементарных преобразований приводим расширенную матрицу к ступенчатому виду

(A\B)~ ,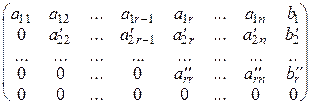

причем rg(A\B) равен числу ненулевых строк в ступенчатой матрице.

Возможны три случая:

1. Получилась строка (0 0 ...0| b_k¢¢),b_k¢¢¹0, ей соответствует уравнение

0=b_k¢¢ - система несовместна (rgA¹ rg(A\B)).

2. Число ненулевых строк r меньше числа неизвестных, тогда система имеет бесчисленное множество решений. Последней ненулевой строке соответствует уравнение a_rr¢¢x_r +...+ a_rn¢¢x_n=b_r¢¢ , из которого находим неизвестное x_r через n-r так называемых свободных неизвестных: x_r+1, ...., x_n. Из уравнений, соответствующих другим строкам, последовательно находим x₁, ..., x_r-1 также через свободные неизвестные.

3. r=n - решение системы единственно. Последней ненулевой строке соответствует уравнение a_nn¢¢x_n = b_n¢¢, из которого находим неизвестное х_n , а далее последовательно - x₁, x₂, ..., x_n-1.

Аналитическая геометрия.

Пусть на плоскости выбрана прямоугольная система координат.

Линия на плоскости может быть задана характерными геометрическими свойствами, по которым находится ее уравнение. Координаты произвольной точки линии являются текущими координатами этой точки, или при помощи уравнения.

Уравнение F(x,y) = 0 называется уравнением линии на плоскости, если ему удовлетворяют координаты (x,y) каждой точки данной линии и не удовлетворяют координаты точек, не лежащих на ней.

Прямая на плоскости в декартовой прямоугольной системе координат Оxy может быть задана уравнением одного из следующих видов.

1. 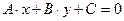– общее уравнение прямой.

2. 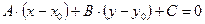– уравнение прямой, проходящей через точку 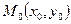перпендикулярно нормальному вектору .

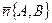3. 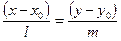– уравнение прямой, проходящей через точку 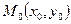параллельно направляющему вектору 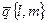(каноническое уравнение прямой).

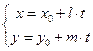
4. 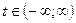– уравнение прямой, проходящей через точку 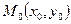параллельно направляющему вектору 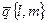(параметрическое уравнение прямой).

5. 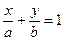– уравнение прямой в отрезках, где a и b – величины направленных отрезков, отсекаемых прямой на координатных осях.

6. 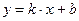– уравнением прямой с угловым коэффициентом k, где k – тангенс угла между прямой и положительным направлением оси абсцисс.

7. 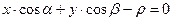– нормальное уравнение прямой, где 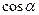, 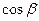– направляющие косинусы нормального вектора 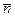направленного из начала координат в сторону прямой, 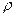– расстояние от начала координат до прямой.

Общее уравнение прямой приводится к нормальному виду путем умножения его на нормирующий множитель 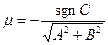, где .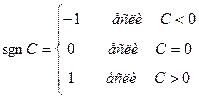

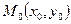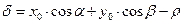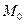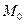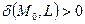
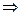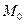Если прямая L задана своим нормальным уравнением, а – некоторая точка плоскости, то выражение задает отклонение точки от прямой L. Знак отклонения указывает на взаимное расположение точки и начала координат относительно прямой L: точка и начало координат лежат по разные стороны относительно прямой L;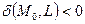 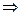точка 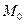и начало координат лежат по одну сторону относительно прямой L;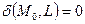 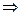точка 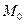лежит на прямой L.

Расстояние от точки 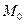до прямой L равно модулю отклонения .

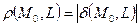Если две прямые L₁ и L₂ заданы уравнениями с угловыми коэффициентами, то тангенс угла между ними может быть определен по формуле: .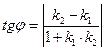

Достаточно часто рассматривается уравнение прямой на плоскости проходящей через две точк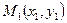и и 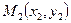, оно имеет вид: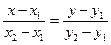

Аналогично линиям на плоскости поверхности могут быть заданы характерными геометрическими свойствами или при помощи уравнений.

Уравнение F(x,y,z)=0 называется уравнением поверхности, если ему удовлетворяют координаты (x,y,z) каждой точки данной поверхности и не удовлетворяют координаты точек, не лежащих на ней.

Плоскость в пространстве в декартовой прямоугольной системе координат Оxyz может быть задана уравнением одного из следующих видов.

1. 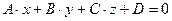– общее уравнение плоскости.

2. 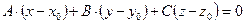– уравнение плоскости, проходящей через точку 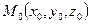перпендикулярно нормальному вектору .

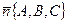3. 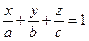– уравнение плоскости в отрезках, где a, b и c – величины направленных отрезков, отсекаемых прямой на координатных осях.

4. 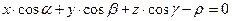– нормальное уравнение плоскости, где 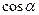, , 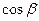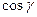– направляющие косинусы нормального вектора 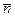направленного из начала координат в сторону плоскости, 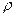– расстояние от начала координат до плоскости.

Общее уравнение плоскости приводится к нормальному виду путем умножения его на нормирующий множитель .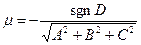

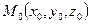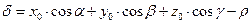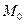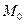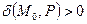
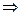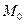Если плоскость P задана своим нормальным уравнением, а – некоторая точка прастранства, то выражение задает отклонение точки от плоскости P. Знак отклонения указывает на взаимное расположение точки и начала координат относительно плоскости P: точка и начало координат лежат по разные стороны относительно плоскости P;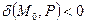 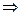точка 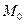и начало координат лежат по одну сторону относительно плоскости P;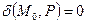 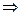точка 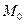лежит на плоскости P.

Расстояние от точки 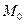до плоскости P равно модулю отклонения .

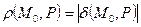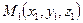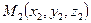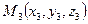Часто рассматривается уравнение плоскости проходящей через три точки , и оно имеет вид: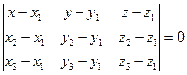

Линию в пространстве можно всегда определить как линию пересечения двух поверхностей. Если они заданы уравнениями F₁(x,y,z)=0 и F₂(x,y,z)=0, то система этих уравнений 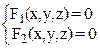задает уравнения линии пересечения поверхностей.

Прямая в пространстве может быть задана при помощи уравнения одного из следующих видов:

1. 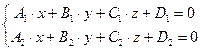– общее уравнение прямой.

2. 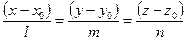– уравнение прямой, проходящей через точку 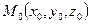параллельно направляющему вектору 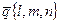(каноническое уравнение прямой).

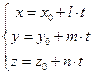
3. 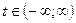– уравнение прямой, проходящей через точку 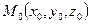параллельно направляющему вектору 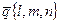(параметрическое уравнение прямой).

Достаточно часто рассматривается уравнение прямой в пространстве проходящей через две точк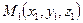и и 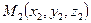, оно имеет вид: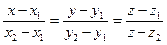

Кривые второго порядка

Общим уравнением кривой второго порядка называется уравнение II степени относительно текущих координат:

Ax²+Bxy+Cy²+2Dx+2Ey+F=0, A²+B²+C² ¹ 0, (A,B,C,D,E,F)Î R

Уравнение кривой второго порядка может определять вырожденную кривую (пустое множество, точку прямую или пару прямых), если же кривая второго порядка не вырожденная, то она представляет из себя эллипс, гиперболу или параболу. В любом случае существует такая декартовая прямоугольная система координат, в которой уравнение этой кривой примет так называемый канонический вид.

Эллипсом называют геометрическое место точек, сумма расстояний от которых до двух данных точек F₁ и F₂, называемых фокусами, есть величина постоянная и равная 2a. Если фокальное расстояние | F₁F₂| =2c, то 2c<2a

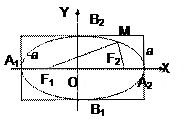Каноническое уравнение эллипса имеет вид: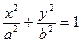

Эллипс симметричен относительно осей координат. Оси симметрии эллипса являются его осями, точка их пересечения - центром эллипса.

Ось, на которой расположены фокусы, называется фокальной. Числа a и b называются большой и малой полуосями эллипса, точки А₁(-a,0), А₂(a,0), B₁(0,-b), B₂(0,b) - вершинами эллипса.

Форму эллипса характеризует отношение c/a=e<1, ( 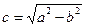) называемое эксцентриситетом эллипса, чем меньше эксцентриситет, тем меньше вытянут эллипс вдоль фокальной оси. В предельном случае при e=0 эллипс переходит в окружность.

Для построения эллипса сначала строится прямоугольник, ограниченный прямыми x=±a, y=±b, затем в него вписывается эллипс.

Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух данных точек F₁ и F₂, называемых фокусами, есть величина постоянная и равная 2a. Если фокальное расстояние |F₁F₂|=2c, то 2c>2a.

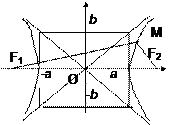Каноническое уравнение гиперболы имеет вид: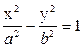

Гипербола симметрична относительно осей координат. Оси симметрии гиперболы являются ее осями. Числа a и b называются соответственно действительной и мнимой полуосями гиперболы, точки А₁(-a,0), А₂(a,0) - вершинами гиперболы.

Форму гиперболы характеризует эксцентриситет c/a=e>1, ( 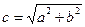) чем меньше эксцентриситет гиперболы, тем более вытянут ее основной прямоугольник в направлении фокальной оси.

Точки гиперболы при удалении их по графику в ¥ приближаются к прямым 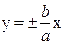, называемым асимптотами гиперболы.

Для построения гиперболы сначала строится прямоугольник, ограниченный прямыми x=±a, y=±b, затем проводятся его диагонали, которые совпадают с асимптотами гиперболы.

Параболой называется геометрическое место точек, равноудаленных от т. F, называемой фокусом, и прямой, называемой директрисой (т. FÏ директрисе).

Расстояние от т. F до директрисы обозначим через p (параметр параболы).

Y

M

Каноническое уравнение гиперболы имеет вид: y²=2px.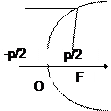

Ось OX является осью симметрии параболы, причем x³0, и график располагается справа от оси OY. ТочкаО(0,0) называется вершиной параболы.

Формулы преобразования координат, которые позволяют повернуть систему на угол j, имеют вид: 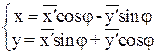, а формулы параллельного переноса начала координат в точку (a,b) имеют вид: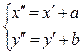

Таким образом, для приведения уравнения кривой второго порядка к каноническому виду целесообразно сначала повернуть систему координат на угол j, таким образом, чтобы избавиться от смешанного произведения переменных, а после этого переместить начало координат методом выделения полных квадратов таким образом, чтобы получилось каноническое уравнение.

Математический анализ

Множеством называют совокупность элементов объединенных, каким либо общим свойством. Множества обозначаются заглавными буквами X, Y, A, B; их элементы - строчными x, y, a, b; xÎX - означает, что элемент х принадлежит множеству Х, хÏХ - не принадлежит; АÌВ - множество А состоит из части элементов множества В, т.е. является подмножеством В.

Множества А и В называют равными, если АÌВ и ВÌА.

Объединением АÈВ множеств А и В называется множество, состоящее из элементов, входящих или в А или в В; пересечением АÇВ называется множество, состоящее из элементов, входящих в А и в В; разностью А\В множеств А и В называется подмножество множества А элементов, не входящих в В. Если ВÌА, то`В=А\В называется дополнением множества А до множества А

Пустое множество (множество, не содержащее ни одного элемента) обозначается символом Æ.

Считают, что между множествами Х и Y установлено соответствие (обозначение X 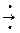Y), если для любого xÎX указаны соответствующие ему yÎY.

Соответствие между X и Y называется взаимно-однозначным, если для любого xÎX существует единственный элемент yÎY и наоборот, для любого yÎY существует единственный элемент xÎX (обозначение Х 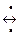Y).

Два множества X и Y называются эквивалентными или имеющими одинаковую мощность (X~Y), если между ними можно установить взаимно-однозначное соответствие.

Множество, эквивалентное множеству натуральных чисел, называется счетным.

Для сокращения записи математических высказываний употребляется символика математической логики. Пусть a, b - некоторые высказывания, относительно которых можно сказать, истинны они или ложны.

Запись `a означает “не a“, т.е. отрицание a;

aÞb - “из a следует b“ (Þ - символ импликации);

aÛb - “a эквивалентно b“ (Û - символ эквивалентности);

aÙb - “ a и b“ (Ù - символ конъюнкции);

aÚb - “ a или b“ (Ú - символ дизъюнкции);

"xÎA - “для любого xÎA” (" - квантор всеобщности);

$ yÎB - “существует yÎB” ($ - квантор существования);

" xÎA: a - “для любого х из А имеет место a“;

$! xÎХ - “существует единственный х из Х”.

d - окрестностью U_d(a) точки аÎR называется интервал (а-d,а+d) (d>0), dÎR. Проколотой d - окрестностью U_d(a) называется множество U_d(a)\{a}

Точка аÎА называется внутренней точкой множества А, если $(d>0: U_d(a)ÌА. Множество А называется открытым, если оно состоит из внутренних точек.

Функцией y=f(x), определенной на множестве Х и принимающей значения на множестве Y, называется такое соответствие между этими множествами, при котором для каждого xÎХ существует единственный элемент yÎY: y=f(x), xÎХ, yÎY ÛX 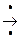Y: " xÎХ$! yÎY

Функция y=f(x) называется возрастающей на [a,b], если большему значению аргумента соответствует большее значение функции : x₁<x₂, x₁,x₂Î[a,b] Þ f(x₁)<f(x₂), убывающей на [a,b], если x₁<x₂, x₁,x₂Î[a,b] Þ f(x₁)>f(x₂). Функция только возрастающая или убывающая на [a,b], называется монотонной.

Функция x=f^-1(y) называется обратной к функции y=f(x), устанавливающей взаимно-однозначное соответствие между X=D(f) и Y=E(f) ( 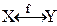), если x=f^-1(y) выражает то же соответствие, причем Y=D(f^-1), X=E(f^-1)

Сложной функцией y=j[y(x)] ( или суперпозицией) называется такая функция, для которой : y=j(z), yÎY, zÎZ, z=y(x), xÎX, zÎZ Þy=(j_°y)x.

Последовательностью называется числовая функция, определенная на множествеNнатуральных чисел, т.е. x_n=f(n).

Теория пределов

Число a называется пределом последовательности x_n при неограниченном возрастании n (a= 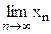), если для любого числа e>0 найдется номер N, зависящий только от e и такой, что при n³N(e) выполняется неравенство |x_n-a|<e

Символическая запись определения: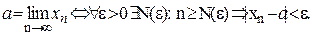

Число b называется пределом функции y=f(x) при х®a, если для любого числа e>0 существует такое число d, зависящее только от e, что из неравенства 0<|x - a|<d следует неравенство |f(x) - b|< e.

Символическая запись определения:

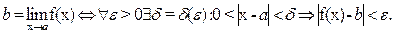
Аналогично определению предела последовательности можно ввести и предел функции при х®¥.

Теоремы о правилах предельного перехода.

Предел постоянной равен самой постоянной.

Для того чтобы 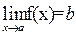, необходимо и достаточно выполнение равенства f(x)=b + a(x), где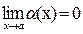

Предел суммы конечного числа функций, имеющих пределы при x®a, равен сумме их пределов

Предел произведения конечного числа функций, имеющих пределы при x®a равен произведению пределов

Постоянный множитель можно выносить за знак предела.

Предел отношения двух функций, имеющих пределы при x®a, равен отношению их пределов (если предел знаменателя не нуль).

Если j(x)£f(x)£y(x) в окрестности т.а и 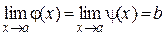, то и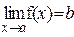

Основные теоремы о пределах облегчают нахождение пределов. В простейших случаях оказывается достаточным подставить в функцию предельное значение аргумента. Если же при такой подстановке получается неопределенное выражение вида , то нахождение предела для таких случаев называют раскрытием неопределенности.

При раскрытиях неопределенностей используются методы вынесения общего множителя за скобку и его сокращение (причем за скобку стремятся вынести такой множитель после сокращения которого предел считается простой подстановкой).

Кроме того в некоторых случаях неопределенности раскрываются с использованием так называемых I и II замечательных пределах.

I замечательный предел: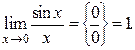

II замечательный предел: .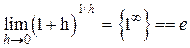

е»2,71828... Логарифмы чисел по основанию е обозначаются lnx и называются натуральными логарифмами.

Пусть функция y=f(x) определена в т. x₀ и ее окрестности: y₀=f(x₀). Если аргумент x получит приращение Dx в т. x₀, т.е. x=x+Dx-новое значение, то и функция получит приращение Dy. Новое значение функции будет y₀+Dy=f(x₀+Dx), а приращение функции в т.x₀ Dy= f(x₀+Dx)-f(x₀)

Функция y=f(x) называется непрерывной в т.x₀, если: она определена в т. х₀ и ее окрестности; .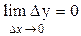

Функция y=f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.

Точка х₀ называется точкой разрыва функции y=f(x), если функция не является непрерывной в т. х₀

Предел 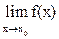, если х®х₀, оставаясь меньше х₀, называется левосторонним пределом и обозначается , предел при х®х₀, х>х₀, называется правосторонним пределом и обозначается ·

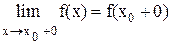Точки разрыва бывают трех типов:

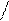1) х₀- устранимая т.р. Û$f(x₀-0)=f(x₀+0) и они конечны, но f(x₀) $.

2) х₀ - т.р. 1 рода f(x₀+0), f(x₀-0) - конечны, но f(x₀+0)¹f(x₀-0).

3) х₀ - т.р. 2 рода: все остальные т.р.

Если функция f(x) непрерывна на [a,b], то она достигает на [a,b] своего наибольшего М и наименьшего m значений (m£f(x)£M), т.е. непрерывная на [a,b] функция ограничена на [a,b].

Если функция ) непрерывна на [a,b] и на концах [a,b] принимает значения разных знаков, то $cÎ[a,b], в которой f(c)=0

Если f(x)Î ) непрерывна на [a,b], f(a)¹f(b), то для любого числа m между f(a) и f(b) найдется т. xÎ (a,b), в которой f(x)=m.Таким образом, непрерывная функция на [a,b] принимает все свои промежуточные значения.