Понятие сложной функции
Глава I. Производная и ее приложения.
Формулы дифференцирования.
Справочный материал.
Пусть функция y=f(x) определена на промежутке Х. Если аргумент изменяется от фиксированного значения х до нового значения 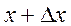
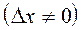 , то значение функции изменяется от
, то значение функции изменяется от 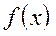 до
до 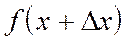 .
.
Определение 1.1. Дифференциальным отношением называется отношение приращения функции к приращению аргумента
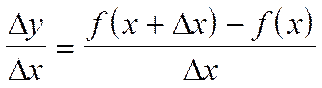
Определение 1.2. Дифференциальное отношение измеряет среднюю скорость изменения функции y=f(x).
Определение 1.3. Производной функции y=f(x) в некоторой точке x называется предел отношения приращения функции к приращению аргумента при 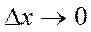 (если этот предел существует)
(если этот предел существует)
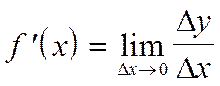
Определение 1.4. Процесс нахождения производной называется дифференцированием.
Производную обозначают символами
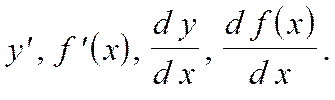
Таблица производных элементарных функций.
1. 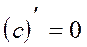
2. 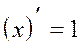
3. 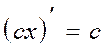
4. 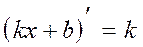
5. 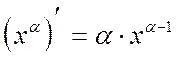
6. 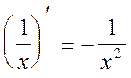
7. 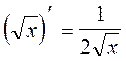
8. 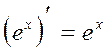
9. 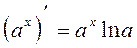
10. 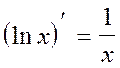
11. 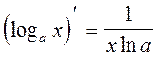
12. 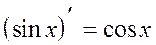
13. 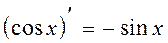
14. 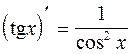
15. 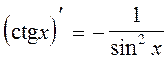
16. 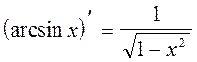
17. 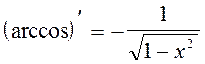
18. 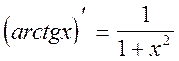
19. 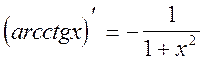
Пример 1.1. Вычислить производные:
1) 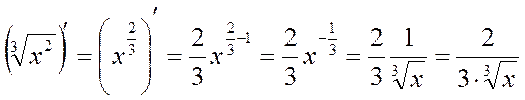
по формулам 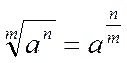
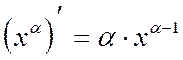 где
где 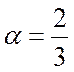
2) 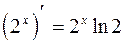 (по формуле
(по формуле 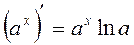 , где a=2)
, где a=2)
3) 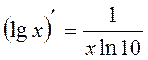 (по формуле
(по формуле 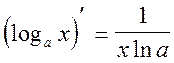 , где a=10)
, где a=10)
Производная суммы.
Определение 1.5.Производная суммы двух дифференцируемых в точке x функций u(x) и v(x) существует в этой точке и вычисляется по формуле:
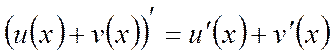
или короче
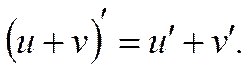 (1)
(1)
Пример 1.2. Вычислить производные:
1. 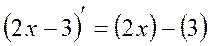 =2-0=2 (по формулам
=2-0=2 (по формулам 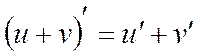 ,
, 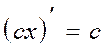 ,
, 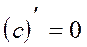 )
)
2. 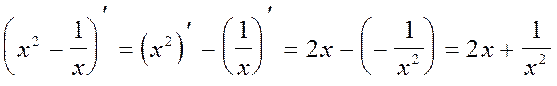
(по формулам 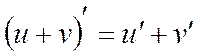 ,
, 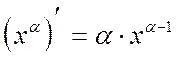 ,
, 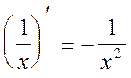 )
)
3. 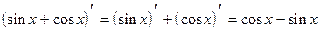
4. 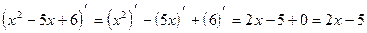
5. 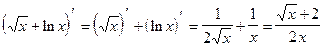
6. 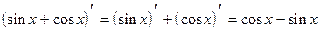
Производная произведения.
Определение 1.6.Производная произведения двух дифференцируемых в точке x функций u(x) и v(x) существует в этой точке и вычисляется по формуле:
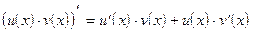
или короче
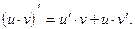 (2)
(2)
Утверждение 1.1Если функция u=u(x) дифференцируема в точке х, а С – постоянная, то функция Cu дифференцируема в этой точке и
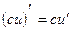 (3)
(3)
или короче: постоянный множитель можно выносить за знак производной.
Доказательство самостоятельно
Пример 3. Найти 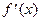 :
: 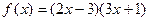 .
.
Решение. 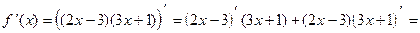
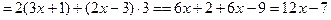 .
.
Была использована формула 4: 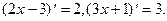
Производная частного.
Определение 1.6Производная частного двух дифференцируемых в точке x функций u(x) и v(x) при условии, что функция v(x) не равна нулю в этой точке, существует в этой точке и вычисляется по формуле:
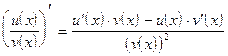
или короче
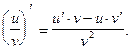 (4)
(4)
Пример 4. Найти значение производной функции 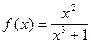 в точке х = 1:
в точке х = 1:
Решение.
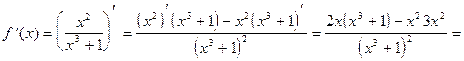
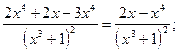
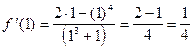
Ответ: 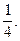
Понятие сложной функции.
Пример 5. Пусть требуется вычислить значение функции 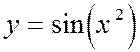 в некоторой фиксированной точке x. Для этого нужно:
в некоторой фиксированной точке x. Для этого нужно:
1) вычислить 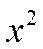 ;
;
2) найти значение синуса при полученном значении 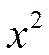 .
.
Иными словами, сначала надо найти значение функции 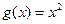 , а затем
, а затем 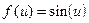 , аргумент u ( u =g(x))в этом случае называют промежуточным, а x – независимой переменной.
, аргумент u ( u =g(x))в этом случае называют промежуточным, а x – независимой переменной.
Пусть функция u=g(x) определена на некотором множестве X, а функция y=f(u) – на множестве значений функции u=g(x), тогда на множестве X определена функция y=f(g(x)), называемая сложной функцией.
Пример 6. Рассмотрим функцию 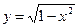 . Чтобы найти значение этой функции в фиксированной точке х, нужно сначала найти значение функции g(x) = 1 - x2, а потом найти значение
. Чтобы найти значение этой функции в фиксированной точке х, нужно сначала найти значение функции g(x) = 1 - x2, а потом найти значение 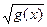 . В этом примере
. В этом примере 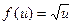 , где u = 1 - x2.
, где u = 1 - x2.
Пример 7. Составить сложную функцию 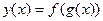 , если
, если 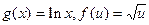 .
.
Решение. 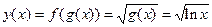 .
.
