Расчет болтовых и заклепочных соединений

Лекция 3

Сдвиг и кручение

Учебные вопросы

СдВИГ и срез

КРУЧЕНИЕ ВАЛОВ КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

3.ПОСТРОЕНИЕ ЭПЮР КРУТЯЩИХ МОМЕНТОВ

НАПРЯЖЕНИЯ И РАСЧЕТ НА ПРОЧНОСТЬ

Сдвиг

Кроме деформации растяжения или сжатия материал, нагруженного элемента конструкции, может испытывать деформацию сдвига.В сплошном материале деформацию сдвига можно осуществить, например, если подвергнуть кручению тонкостенную трубу (рис. 5.1, а).Прямоуголь­ные до деформации элементы материала стенок трубы превращаются в параллелограммы за счет изменения первоначально прямого угла на малый угол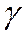 ,называ­емый углом сдвига.

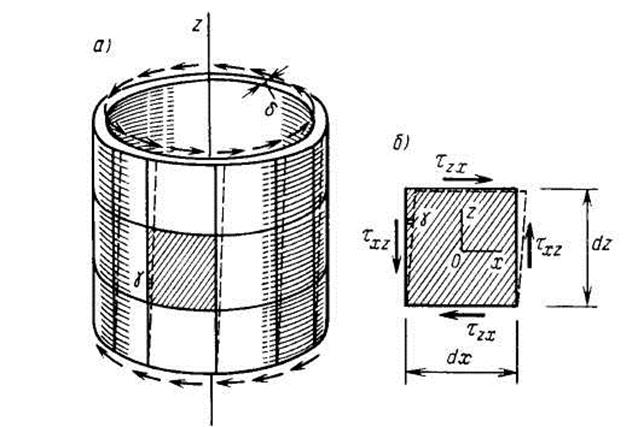
Рис. 5.1

На рис. 5.1, б показан элемент, выделенный из стенки трубы. Компоненту касательных напряжений, возника­ющих на горизонтальных площадках в окружном направ­лении, обозначим 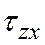. Одни напряжения 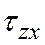существовать на гранях элемента не могут, так как они, образуя пару сил с моментом ( 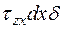)dz, где в скобках дано значение касательных сил

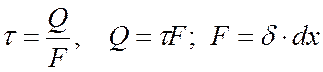( ), adz — плечо пары сил, вызвали бы вращение элемента. Поэтому на вертикальных гранях указаны компоненты напряжений 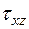, приводящиеся к па­ре ( 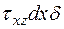)dх. Найдем соотношение этих напряжений из условия равновесия элемента в виде равенства нулю суммы моментов этих пар:

.

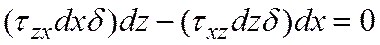Сократив это выражение на произведение 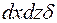,по­лучим равенство

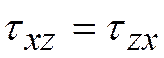, (5.1)

называемое законом парности касательных напряжений: на взаимно перпендикулярных площадках касательные напряжения численно равны и направлены так, что стре­мятся вращать элемент в противоположные стороны. Подчеркнем, что в общем случае на каждой площадке могут возникать две компоненты касательных напряже­ний, например 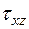и 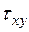. В законе о парности идет речь о компонентах, перпендикулярных линии пересечения ортогональных площадок.

Таким образом, в плоскости могут быть только два варианта действия касательных напряжений на гранях прямоугольного элемента материала, отличающиеся на­правлением векторов напряжений .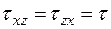

Напряженно-деформированное состояние, характери­зуемое тем, что на гранях элемента возникают только касательные напряжения, называют чистым сдвигом.

Все элементы стенки трубы на рис. 5.1, находятся в одинаковых условиях и испытывают чистый сдвиг.

Закон Гука при сдвиге.Экспериментальное изучение деформации чистого сдвига обычно проводят путем кру­чения трубчатых образцов, подобных показанному на рис. 5.1, а, б, получая из эксперимента зависимость между напряжением 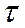и углом сдвига 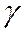. Такая диаграмма сдвига изображена на рис. 2 для пластичной стали. Для напряжения 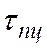, называемого пределом пропорциональности при сдвиге, справедлива линейная зависимость, которая носит название закона Гука при сдвиге.

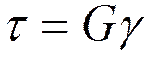, (5.2)

где G – модуль упругости второго рода; 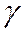- угол сдвига.

Напряжение 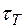является пределом текучести при сдвиге, т. е. касательным напряжением, при котором угол сдвига воз­растает при постоянном напряжении. Для пластичного материала протяженность диаграммы сдвига довольно велика (на рис. 5.2 отмечено пунктиром). Завершается испытание в этом случае срезом материала в плоскости поперечного сечения трубчатого образца.

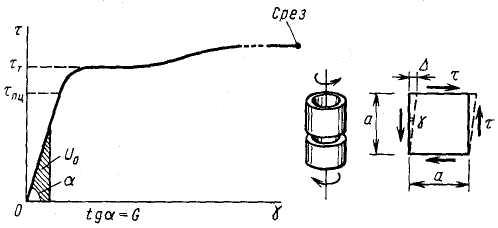
Рис. 5.2 – Диаграмма сдвига для пластичной стали

В формуле (5.2) G— это модуль упругости материала при сдвиге. Смещение 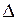(рис. 5.2) называют абсолютным сдвигом, а отношение

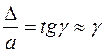
— относительным сдвигом или, как указывалось, углом сдвига. Эта вели­чина безразмерная, поэтому модуль сдвига G выражается в единицах напряжения (Па). Теоретически доказана формула, связывающая для изотропного мате­риала три константы упругости: Е — модуль упругости при растяжении; 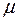— коэффициент Пуассона; G— мо­дуль сдвига, а именно:

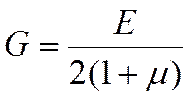. (5.3)

Например, для стали Е=200 ГПа, 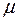=0,25 и по формуле (5.3) найдем, что G=80 ГПа. Зависимость (5.3) подтвер­ждается экспериментально. Характерно, что для многих материалов предел текучести при сдвиге 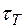связан с преде­лом текучести при растяжении 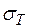следующим соотноше­нием:

.

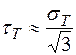Расчет болтовых и заклепочных соединений

Болты и заклепки применяются для соединения между собой элементов металлических конструкций. Наиболее часто встреча­ющиеся типы соединений, передающие растягивающую или сжимающую силу, показаны на рис. 5.3. На рис. 5.3, а показано соединение двух листов внахлестку, где каждый болт или зак­лепка при разрушении срезается по одной из плоскостей кон­такта соединяемых листов. Такие болты и заклепки называются односрезными.

На рис. 5.3, б показано соединение встык листов с одной на­кладкой. Болты или заклепки также односрезные. На рис. 5.3, в показано соединение встык с двумя накладками. Срез происхо­дит по двум плоскостям контакта накладок и соединяемых ли­стов. В этом случае болты и заклепки являются двухсрезными.

В методах расчета болтов и заклепок нет принципиальных различий.

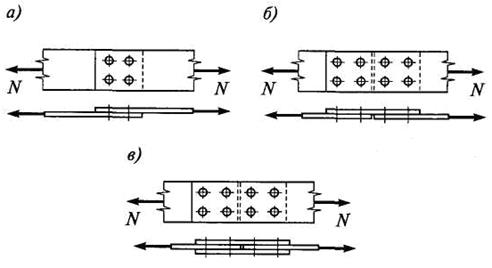
Рис. 5.3

В качестве примера рассмотрим работу односрезного болта или заклепки, соединяющей два листа (рис. 5.4, а, б).

При расчете предполагается, что касательные напряжения равномерно распределены по площади среза болта или заклеп­ки. Площадь среза односрезного болта или заклепки диаметром d равна 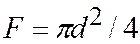. Тогда расчетное усилие, которое может быть воспринято односрезным болтом или заклепкой из условия прочности при срезе, определяется по формуле

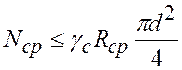, (5.3)

где 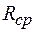— расчетное сопротивление материала болта или заклеп­ки на срез, 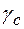— коэффициент условий работы.

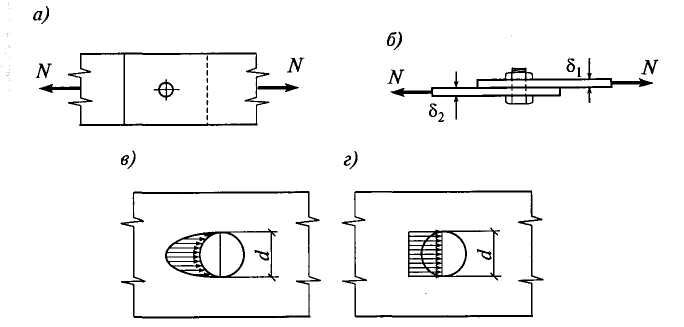
Рис. 5.4

Помимо среза возможно нарушение соединения вследствие смятия болта, заклепки или соединяемых листов в месте их контакта. Под смятием понимают местные пластические дефор­мации, происходящие на поверхностях контакта. Смятие проис­ходит по полуцилиндрической поверхности контакта, и напряже­ния смятия распределяются по ней неравномерно (рис. 5.4, в). Для упрощения в расчет вводится условное напряжение смятия, равномерно распределенное по площади диаметрального сече­ния F= dδ (рис. 5.4, г), где δ— меньшая из толщин соединяе­мых листов. Тогда расчетное усилие, которое может быть воспринято опре­деляется по формуле

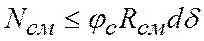, (5.4)

где 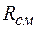— расчетное сопротивление смятию соединяемых элементов.

За расчетное усилие, которое может быть воспринято соеди­нением, принимается меньшее из усили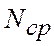й и .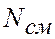

В общем случае, когда стык состоит из нескольких элемен­тов, соединенных болтами или заклепками, предполагается, что продольное усилие, действующее на соединение, распределяет­ся поровну между болтами или заклепками.

Расчетные усилия, которые могут быть восприняты соедине­нием из условий прочности на срез и смятие, определяются по формулам

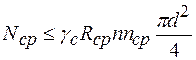; (5.5)

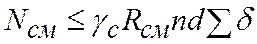, (5.6)

где п— число болтов или заклепок, работающих в одном на­правлении; 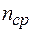— число плоскостей среза болта или заклепки; 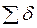— наименьшая суммарная толщина элементов, сминаемых в одном направлении.

Расчетные сопротивления на срез болтов и на смятие эле­ментов, соединяемых болтами, коэффициенты условий работы и конструктивные рекомендации (выбор типов и диаметров болтов, их размещение и т.п.) приведены в СНиП.