Необходимые и достаточные условия сходимости числовых рядов
Раздел 7. Числовые и степенные ряды
Числовые ряды
Основные определения
Определение. Пусть 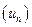 - произвольная числовая последовательность. Формальное выражение вида
- произвольная числовая последовательность. Формальное выражение вида
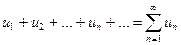
называется числовым рядом. Числа 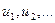 называются членами ряда, а
называются членами ряда, а 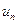 – общим членом ряда.
– общим членом ряда.
Определение. Суммы 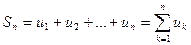 ,
, 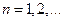 называются частичными суммами ряда.
называются частичными суммами ряда.
Определение. Ряд 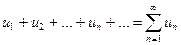 называется сходящимся, если существует конечный предел
называется сходящимся, если существует конечный предел 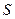 последовательности
последовательности 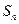
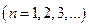 его частичных сумм. При этом число
его частичных сумм. При этом число 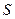 называется суммой ряда:
называется суммой ряда:
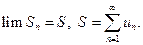
Определение. Если последовательность частичных сумм 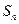
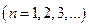 ряда
ряда 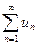 не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся.
не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся.
Свойства числовых рядов
1) Сходимость или расходимость ряда не нарушится, если отбросить или добавить произвольное конечное число членов ряда.
2) Рассмотрим два ряда 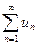 и
и 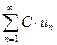 , где С – постоянное число.
, где С – постоянное число.
Теорема. Если ряд 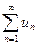 сходится и имеет сумму равную S, то ряд
сходится и имеет сумму равную S, то ряд 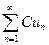 также сходится, и имеет сумму равную
также сходится, и имеет сумму равную 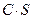
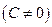 .
.
3) Рассмотрим два ряда 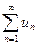 и
и 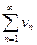 . Суммой (разностью) этих рядов называется ряд
. Суммой (разностью) этих рядов называется ряд 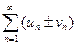 , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды 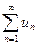 и
и 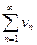 сходятся и их суммы равны соответственно
сходятся и их суммы равны соответственно 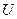 и
и 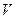 , то ряд
, то ряд 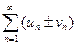 тоже сходится и его сумма равна
тоже сходится и его сумма равна 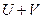 .
.
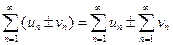
Сумма (разность) двух сходящихся рядов также является сходящимся рядом.
Сумма сходящегося и расходящегося рядов является расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Необходимые и достаточные условия сходимости числовых рядов
Теорема.(Критерий Коши) Для того, чтобы последовательность 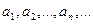 была сходящейся, необходимо и достаточно, чтобы для любого
была сходящейся, необходимо и достаточно, чтобы для любого 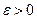 существовал такой номер N, что при
существовал такой номер N, что при 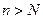 и любом p > 0, где р – целое число, выполнялось неравенство:
и любом p > 0, где р – целое число, выполнялось неравенство:
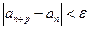 .
.
Доказательство. (необходимость) Пусть 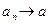 , тогда для любого числа
, тогда для любого числа 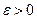 найдется номер N такой, что неравенство
найдется номер N такой, что неравенство 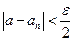 выполняется при
выполняется при 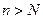 . При
. При 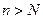 и любом целом
и любом целом 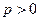 выполняется также неравенство
выполняется также неравенство 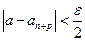 . Учитывая оба неравенства, получаем:
. Учитывая оба неравенства, получаем:
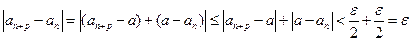
Необходимость доказана. Доказательство достаточности рассматривать не будем.
Сформулируем критерий Коши для ряда.
Для того чтобы ряд 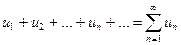 был сходящимся, необходимо и достаточно, чтобы для любого
был сходящимся, необходимо и достаточно, чтобы для любого 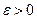 существовал номер N такой, что при n>N и любом p>0 выполнялось бы неравенство
существовал номер N такой, что при n>N и любом p>0 выполнялось бы неравенство
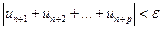 .
.
Однако на практике использовать непосредственно критерий Коши не очень удобно, поэтому, как правило, используются более простые признаки сходимости.
Теорема.(Необходимый признак сходимости ряда). Если ряд 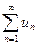 сходится, то его общий член un стремился к нулю при
сходится, то его общий член un стремился к нулю при 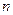 стремящемся к
стремящемся к 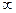 .
.
Это условие не является достаточным. Однако, если общий член ряда не стремится к нулю, то ряд расходится. Например, так называемый гармонический ряд 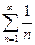 является расходящимся, хотя его общий член и стремится к нулю.
является расходящимся, хотя его общий член и стремится к нулю.
Пример. Исследовать сходимость ряда 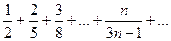
Найдем 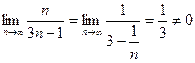 - необходимый признак сходимости не выполняется, значит ряд расходится.
- необходимый признак сходимости не выполняется, значит ряд расходится.
Теорема.Если ряд сходится, то последовательность его частичных сумм ограничена.
Это условие не является достаточным.
Например, ряд 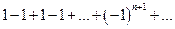 расходится, т.к. расходится последовательность его частичных сумм в силу того, что
расходится, т.к. расходится последовательность его частичных сумм в силу того, что
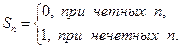
Однако при этом последовательность частичных сумм ограничена, т.к. 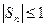 при любом n.
при любом n.
