Третье начало термодинамики
Третье начало термодинамики было сформулировано в 1906 году немецким физиком и химиком Вольтером Фридрихом Германом Нернстом (1864 - 1941) эмпирическим путем на основе обобщения экспериментальных данных и получило название теоремы Нернста:
При стремлении температуры любой равновесной термодинамической системы к абсолютному нулю ее энтропия стремится к некоторой универсальной постоянной величине, значение которой не зависит от каких-либо термодинамических параметров системы и может быть принято равной нулю:
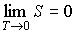 . | (3.62) |
В дополнение к условию (3.62) из утверждения теоремы Нернста о независимости значения энтропии равновесной системы при абсолютном нуле температуры от ее термодинамических параметров следует также выражение:
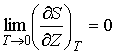 , | (3.63) |
где 
- любой термодинамический параметр системы, например, объем, давление и т.д. Здесь нижний индекс 
за скобками обозначает дифференцирование при постоянном значение величины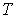 
.
Теорема Нернста применима только для систем, находящихся в состоянии термодинамического равновесия и не справедлива для неравновесных систем. В частности, при стремлении температуры аморфного тела, например, стекла, к абсолютному нулю, его энтропия не стремится к некоторому определенному постоянному значению. В зависимости от того, как осуществляется процесс охлаждения, энтропия аморфного тела при стремлении к абсолютному нулю будет различной. Это связано с тем, что для аморфных тел, которые находятся в неравновесном (метастабильном) состоянии, процесс охлаждения может происходить быстрее, чем переход их в равновесное (кристаллическое) состояние.
Из третьего начала термодинамики непосредственно следует недостижимость температуры равной абсолютному нулю. Действительно, для того, чтобы практически осуществить охлаждение термодинамической системы до абсолютного нуля температуры, необходимо чередовать изотермическое сжатие и адиабатическое расширение. При первом процессе происходит отвод теплоты, а при втором - уменьшение температуры системы. Но, если изотермический процесс при 
приведет к отводу некоторого конечного количества теплоты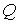 
, то в соответствии с формулой (3.53)это вызовет достаточно большое, в пределе бесконечное изменение энтропии. Это противоречит теореме Нернста, так как в соответствии с (3.63) изменение энтропии в изотермическом процессе при тоже стремится к нулю. Следовательно, охлаждение термодинамической системы до абсолютного нуля температуры невозможно.
Другим следствием третьего начала термодинамики является невозможность использования уравнения Клапейрона-Менделеева (2.10) для описания идеального газа при температурах, близких к абсолютному нулю. Так как для идеального газа на основании первого начала термодинамики (1.5) можно записать:
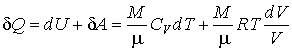 , | (3.64) |
то определение энтропии с помощью интеграла (3.53) дает:
 , | (3.65) |
где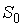 
- произвольная постоянная интегрирования. Здесь из соображений размерности введены величины 
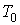и 
, которые можно считать равными единице в системе СИ: 
К и 
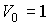м3.
Таким образом, при энтропия, вычисленная по формуле (3.65), не принимает нулевого значения, а стремится к минус бесконечности. А это противоречит третьему началу термодинамики, что делает невозможным применение уравнения Клапейрона-Менделеева для описания газа при температурах, близких к абсолютному нулю. Состояние газа при называется вырожденным состоянием и для его описания требуется применение законов, следующих из уравнений квантовой статистики.
10) Идеальный газ уравнения процесса