Корреляционный момент и корреляция
Случайных величин
Пусть  и
и  - две случайные величины. Положим,
- две случайные величины. Положим,
 =
=  +
+ 
По теореме сложения математических ожиданий будем иметь:
М  = М
= М  + М
+ М 
Вычитая это равенство из предыдущего, получим:
 =
=  +
+ 
где  обозначает отклонение величины
обозначает отклонение величины  от m
от m  , то есть
, то есть
 - m
- m  . Отсюда
. Отсюда
 2 =
2 =  2 +
2 +  2 + 2
2 + 2 

Найдем теперь дисперсию величины  +
+  :
:
D(  +
+  ) = D
) = D  = M
= M  2 = M
2 = M  2 + M
2 + M  2 + 2M
2 + 2M 
 =
=
= D  + D
+ D  + 2M(
+ 2M( 
 ) (1)
) (1)
Число M( 
 ) имеет особое значение для характеристики системы (
) имеет особое значение для характеристики системы (  ,
,  ). Его называют корреляционным моментом случайных величин
). Его называют корреляционным моментом случайных величин  и
и и обозначают через К(
и обозначают через К(  ,
,  ). Таким образом, по определению
). Таким образом, по определению
К(  ,
,  ) = M(
) = M( 
 ).
).
Формула (1) принимает теперь следующий вид:
D(  +
+  ) = D(
) = D(  ) + D(
) + D(  ) + 2K(
) + 2K( 
 ) (2)
) (2)
- дисперсия суммы равна сумме дисперсий плюс удвоенный корреляционный момент.
Корреляционный момент, как свидетельствует его название, (от латинского слова correlation – соответствие, взаимосвязь), играет определенную роль при оценке зависимости  и
и  . Основное свойство корреляционного момента выражается следующим предложением.
. Основное свойство корреляционного момента выражается следующим предложением.
Если величины  и
и  независимы, то их корреляционный момент равен нулю.
независимы, то их корреляционный момент равен нулю.
Действительно, пусть  и
и  независимы. Тогда,
независимы. Тогда,
очевидно, величины  и
и  будут тоже независимы. Отсюда вытекает, что математическое ожидание произведения
будут тоже независимы. Отсюда вытекает, что математическое ожидание произведения 
 будет: M(
будет: M( 
 ) = M
) = M  M
M  =
=  = 0.
= 0.
Из доказанного предложения следует: если К(  ,
,  ) ≠ 0, то величины
) ≠ 0, то величины  и
и  не могут быть независимыми. Таким образом, неравенство нулю корреляционного момента определенно свидетельствует о наличии связи между величинами
не могут быть независимыми. Таким образом, неравенство нулю корреляционного момента определенно свидетельствует о наличии связи между величинами  и
и  .
.
Предположим, что в некотором опыте наблюдаются две случайные величины  и
и  .
.
То обстоятельство, что  и
и  обусловлены одним и тем же опытом, вообще говоря, создает между этими величинами некоторого рода связь: как принято говорить,
обусловлены одним и тем же опытом, вообще говоря, создает между этими величинами некоторого рода связь: как принято говорить,  и
и  скоррелированы (согласованы) друг с другом.
скоррелированы (согласованы) друг с другом.
Одной из характеристик корреляции, как мы уже знаем, служит корреляционный момент 
K( 
 ) = M(
) = M( 
 ) = M((
) = M((  - m
- m  ) (
) (  -
-  )),
)),
где m  и
и  - математические ожидания величин
- математические ожидания величин  и
и  соответственно. Заметим, что справедлива формула
соответственно. Заметим, что справедлива формула
K (  ,
,  ) = M(
) = M( 
 ) - m
) - m 
 ;
;
чтобы получить эту формулу, надо записать
(  - m
- m  )(
)(  -
-  ) =
) = 
 - m
- m 
 -
- 
 + m
+ m 

и приравнять друг к другу математические ожидания левой и правой частей.
Поскольку если величина  и
и  независимы, то их корреляционный момент равен нулю. Поэтому неравенство нулю величины К(
независимы, то их корреляционный момент равен нулю. Поэтому неравенство нулю величины К(  ,
,  ) свидетельствует о наличии связи между
) свидетельствует о наличии связи между  и
и  .
.
Случайные величины  и
и  , для которых корреляционный момент равен нулю, называются некоррелированными. Таким образом, из независимости величин
, для которых корреляционный момент равен нулю, называются некоррелированными. Таким образом, из независимости величин  и
и  следует их некоррелированность. Обратное, вообще говоря, неверно: можно привести примеры
следует их некоррелированность. Обратное, вообще говоря, неверно: можно привести примеры  и
и  , для которых корреляционный момент равен нулю, между тем
, для которых корреляционный момент равен нулю, между тем  и
и  связаны между собой (даже функционально).
связаны между собой (даже функционально).
Приведём пример такого рода. Пусть величина  распределена непрерывно, причём плотность вероятности
распределена непрерывно, причём плотность вероятности  есть чётная функция; величина
есть чётная функция; величина  =
=  2. Тогда М
2. Тогда М  = 0 и значит
= 0 и значит

 K(
K(  ,
,  ) = M(
) = M( 
 ) = M(
) = M(  ) =
) = 
 3
3  dx = 0.
dx = 0.
Корреляционный момент, как следует из его определения, зависит от выбора единиц измерения для  и
и  ; например, если при измерении
; например, если при измерении  и
и  в килограммах было получено значение К = 5 кг2, то, приняв за единицу измерения 1 г, получим для корреляционного момента значение К = 5х106 г2. Это обстоятельство затрудняет сравнение корреляционных моментов различных систем случайных величин. Чтобы преодолеть такое затруднение, вводится другая характеристика связи между
в килограммах было получено значение К = 5 кг2, то, приняв за единицу измерения 1 г, получим для корреляционного момента значение К = 5х106 г2. Это обстоятельство затрудняет сравнение корреляционных моментов различных систем случайных величин. Чтобы преодолеть такое затруднение, вводится другая характеристика связи между  и
и  - коэффициент корреляции.
- коэффициент корреляции.
Определение. Коэффициентом корреляции случайных величин  и
и  называется число
называется число

- отношение корреляционного момента к произведению средних квадратичных отклонений величин  и
и  .
.
Очевидно, коэффициент корреляции не зависит от выбора единиц измерения для величин  и
и  (иначе говоря, r(
(иначе говоря, r(  ,
,  ) есть величина безразмерная). Он не зависит также и от выбора начала отсчета при измерении
) есть величина безразмерная). Он не зависит также и от выбора начала отсчета при измерении  и
и  .
.
Имеет место следующая теорема.
Теорема. Коэффициент корреляции всегда заключен между -1 и 1:
-1  r
r  1
1
В случае, когда r = 1, величины  и
и  связаны линейной зависимостью:
связаны линейной зависимостью:
 = a
= a  + b (a, b = const),
+ b (a, b = const),
причем a>0; при r = -1 между величинами  и
и  имеет место линейная зависимость c a <0.
имеет место линейная зависимость c a <0.
Доказательство. Рассмотрим математическое ожидание случайной величины
(  + t
+ t  )2,
)2,
где  =
=  -
-  ,
,  =
=  - m
- m  , а t – любое действительное число. Имеем:
, а t – любое действительное число. Имеем:
M(  +
+ 
 )2 = M(
)2 = M(  2 + 2t
2 + 2t 
 + t2
+ t2  2) = M
2) = M  2 +2t M(
2 +2t M( 
 ) + +t2M
) + +t2M  2 = D
2 = D  + 2tK(
+ 2tK(  ,
,  ) + t2D
) + t2D  .
.
Мы получим равенство вида
M(  +
+ 
 )2 =
)2 = 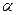 t2 + 2
t2 + 2  t +
t +  (3)
(3)
где 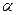 = D
= D  ,
,  = K(
= K(  ,
,  ),
),  = D
= D  . Квадратный трехчлен, стоящий в правой части этого равенства, при любом значении t неотрицателен (ибо он равен математическому ожиданию случайной величины, принимающей только неотрицательные значения). Отсюда вытекает, что дискриминант этого трехчлена, т. е. выражение
. Квадратный трехчлен, стоящий в правой части этого равенства, при любом значении t неотрицателен (ибо он равен математическому ожиданию случайной величины, принимающей только неотрицательные значения). Отсюда вытекает, что дискриминант этого трехчлена, т. е. выражение
 2 -
2 -  ,
,
есть число не положительное. Итак,
К2(  ,
,  ) – D
) – D  D
D 
 0,
0,
или

Мы пришли к неравенству r2  1, означающему, что величина r заключена в промежутке от 1 до -1.
1, означающему, что величина r заключена в промежутке от 1 до -1.
Предположим теперь, что r2 – 1, т. е. r равно -1 или 1.
В этом случае дискриминант указанного выше квадратного трехчлена равен нулю. Отсюда вытекает, что трёхчлен имеет действительный корень, т. е. при некотором действительном значении t = -a выражение 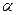 t2 + 2
t2 + 2  t +
t +  равно нулю. Но тогда в силу (3) мы должны иметь:
равно нулю. Но тогда в силу (3) мы должны иметь:
M(  +
+ 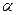
 )2 = 0
)2 = 0
а это в свою очередь означает:
 - a
- a  = 0
= 0
или
 = a
= a  + b.
+ b.
Обратно, допустим, что между случайными величинами  и
и  имеет место такого рода соотношение. Изменив начало отсчёта величины
имеет место такого рода соотношение. Изменив начало отсчёта величины  (что не влияет на r), можно добиться, чтобы было b = 0, т. е.
(что не влияет на r), можно добиться, чтобы было b = 0, т. е.  = a
= a  . В этом случае, как легко проверить, величина r будет равна -1, если a < 0, и 1, если a > 0.
. В этом случае, как легко проверить, величина r будет равна -1, если a < 0, и 1, если a > 0.
Установленные нами свойства коэффициента корреляции дают основание для некоторого качественного заключения, а именно: близость величины r2 к единице есть признак того, что зависимость между  и
и  близка к линейной. Если при этом r > 0, то с возрастанием
близка к линейной. Если при этом r > 0, то с возрастанием  возрастает в среднем и
возрастает в среднем и  , тогда говорят о положительной корреляции между величинами
, тогда говорят о положительной корреляции между величинами  и
и  ; если же r < 0, то при возрастании
; если же r < 0, то при возрастании  величина
величина  в среднем убывает (отрицательная корреляция).
в среднем убывает (отрицательная корреляция).
