Среднее квадратическое отклонение.

Недостатком дисперсии является то, что ее размерность равна размерности квадрата случайной величины, поэтому в ряде случаев для описания разброса используют среднеквадратическое отклонение, которое имеет ту же размерность, что и сама случайная величина.

Средним квадратическим отклонением σ(Х) называется арифметическое значение квадратного корня из ее дисперсии:

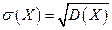
Пример 1: Имеется 10 студенческих групп, насчитывающих соответственно 12, 10, 15, 14, 10, 12, 9, 12, 14, 13. Установить закон распределения дискретной случайной величины Х, представляющей собой число студентов в наугад выбранной группе, построить многоугольник распределения и найти ее числовые характеристики.

X
P

Задача 2: Для функции распределения непрерывной случайной величины

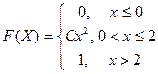
найти коэффициент С и определить вероятность попадания СВХ в интервал [0; 1]. Найти числовые характеристики этой функции

Нормальный закон распределения.

Нормальный закон («закон Гаусса») играет исключительную роль в теории вероятностей. Он наиболее часто встречается на практике.

Говорят, что случайная величина Х имеет нормальное распределение, если плотность распределения вероятностей этой случайной величины имеет вид:

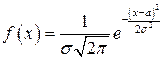
Нормальное распределение зависит от двух параметров a и σ, где

а – математическое ожидание,

σ – среднеквадратическое отклонение (σ > 0).

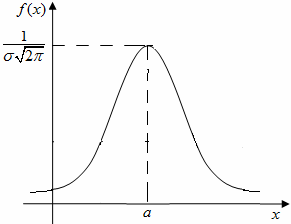
График плотности распределения вероятностей представлен на рисунке.

Формула для нахождения вероятности попадания нормально распределенной случайной величины в заданный интервал:

,

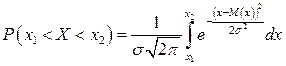
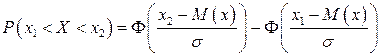где 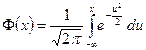- функция Лапласа.

Значения функции Лапласа для х ≥ 0 приведены в специальной таблице. Для вычисления отрицательных значений аргумента необходимо учитывать свойства функции.

Свойства функции Лапласа:

1. Функция Лапласа является нечетной, т.е.

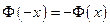
2. .

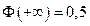На практике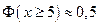

Пример 3: Известно, что у человека рН-уровень крови является случайной величиной, имеющей нормальное распределение с математическим ожиданием 7,4 и дисперсией 0,04. Найти вероятность того, что рН находится между 7,25 и 7,7.

Для нормальной случайной величины характерно свойство, называемое «правилом трех сигм»: вероятность того, что значение нормально распределенной случайной величины отклониться от математического ожидания не более, чем на 3σ, примерно равна единице.

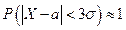
Пример 4:Определим в условиях примера 3 диапазон значений рН крови здорового человека.

Таблица значений функции Лапласа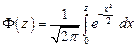

z	Ф(z)	z	Ф(z)	z	Ф(z)	z	Ф(z)
		0,35	0,1368	0,70	0,2580	1,05	0,3531
0,01	0,0040	0,36	0,1406	0,71	0,2612	1,06	0,3554
0,02	0,0080	0,37	0,1443	0,72	0,2642	1,07	0,3577
0,03	0,0120	0,38	0,1480	0,73	0,2673	1,08	0,3599
0,04	0,0160	0,39	0,1517	0,74	0,2704	1,09	0,3621
0,05	0,0199	0,40	0,1554	0,75	0,2734	1,10	0,3643
0,06	0,0239	0,41	0,1591	0,76	0,2764	1,11	0,3665
0,07	0,0279	0,42	0,1628	0,77	0,2794	1,12	0,3686
0,08	0,0319	0,43	0,1664	0,78	0,2823	1,13	0,3708
0,09	0,0359	0,44	0,1700	0,79	0,2852	1,14	0,3729
0,10	0,0398	0,45	0,1736	0,80	0,2881	1,15	0,3749
0,11	0,0438	0,46	0,1772	0,81	0,2910	1,16	0,3770
0,12	0,0478	0,47	0,1808	0,82	0,2939	1,17	0,3790
0,13	0,0517	0,48	0,1844	0,83	0,2967	1,18	0,3810
0,14	0,0557	0,49	0,1879	0,84	0,2996	1,19	0,3830
0,15	0,0596	0,50	0,1915	0,85	0,3023	1,20	0,3849
0,16	0,0636	0,51	0,1950	0,86	0,3051	1,21	0,3869
0,17	0,0675	0,52	0,1985	0,87	0,3079	1,22	0,3888
0,18	0,0714	0,53	0,2019	0,88	0,3106	1,23	0,3907
0,19	0,0754	0,54	0,2054	0,89	0,3133	1,24	0,3925
0,20	0,0793	0,55	0,2088	0,90	0,3159	1,25	0,3944
0,21	0,0832	0,56	0,2123	0,91	0,3186	1,26	0,3962
0,22	0,0871	0,57	0,2157	0,92	0,3212	1,27	0,3980
0,23	0,0910	0,58	0,2190	0,93	0,3238	1,28	0,3997
0,24	0,0948	0,59	0,2224	0,94	0,3264	1,29	0,4015
0,25	0,0987	0,60	0,2258	0,95	0,3289	1,30	0,4032
0,26	0,1026	0,61	0,2291	0,96	0,3315	1,31	0,4049
0,27	0,1064	0,62	0,2324	0,97	0,3340	1,32	0,4066
0,28	0,1103	0,63	0,2357	0,98	0,3365	1,33	0,4082
0,29	0,1141	0,64	0,2389	0,99	0,3389	1,34	0,4099
0,30	0,1179	0,65	0,2422	1,00	0,3413	1,35	0,4115
0,31	0,1217	0,66	0,2454	1,01	0,3438	1,36	0,4131
0,32	0,1255	0,67	0,2486	1,02	0,3461	1,37	0,4147
0,33	0,1293	0,68	0,2518	1,03	0,3485	1,38	0,4162

z	Ф(z)	z	Ф(z)	z	Ф(z)	z	Ф(z)
0,34	0,1331	0,69	0,2549	1,04	0,3508	1,39	0,4177
1,40	0,4192	1,74	0,4591	2,16	0,4846	2,84	0,4977
1,41	0,4207	1,75	0,4599	2,18	0,4854	2,86	0,4979
1,42	0,4222	1,76	0,4608	2,20	0,4861	2,88	0,4980
1,43	0,4236	1,77	0,4616	2,22	0,4868	2,90	0,4981
1,44	0,4251	1,78	0,4625	2,24	0,4875	2,92	0,4983
1,45	0,4265	1,79	0,4633	2,26	0,4881	2,94	0,4984
1,46	0,4279	1,80	0,4641	2,28	0,4887	2,96	0,4985
1,47	0,4292	1,81	0,4649	2,30	0,4893	2,98	0,4986
1,48	0,4306	1,82	0,4656	2,32	0,4898	3,00	0,4987
1,49	0,4319	1,83	0,4664	2,34	0,4904	3,05	0,4989
1,50	0,4332	1,84	0,4671	2,36	0,4909	3,10	0,4990
1,51	0,4345	1,85	0,4678	2,38	0,4913	3,15	0,4992
1,52	0,4357	1,86	0,4686	2,40	0,4918	3,20	0,4993
1,53	0,4370	1,87	0,4693	2,42	0,4922	3,25	0,4994
1,54	0,4382	1,88	0,4700	2,44	0,4927	3,30	0,4995
1,55	0,4394	1,89	0,4706	2,46	0,4931	3,35	0,4996
1,56	0,4406	1,90	0,4713	2,48	0,4934	3,40	0,4997
1,57	0,4418	1,91	0,4719	2,50	0,4938	3,45	0,4997
1,58	0,4430	1,92	0,4726	2,52	0,4941	3,50	0,4998
1,59	0,4441	1,93	0,4732	2,54	0,4945	3,55	0,4998
1,60	0,4452	1,94	0,4738	2,56	0,4948	3,60	0,4998
1,61	0,4463	1,95	0,4744	2,58	0,4951	3,65	0,49987
1,62	0,4474	1,96	0,4750	2,60	0,4953	3,70	0,49989
1,63	0,4485	1,97	0,4756	2,62	0,4956	3,75	0,49991
1,64	0,4495	1,98	0,4762	2,64	0,4959	3,80	0,49993
1,65	0,4505	1,99	0,4767	2,66	0,4961	3,85	0,49994
1,66	0,4515	2,00	0,4773	2,68	0,4963	3,90	0,49995
1,67	0,4525	2,02	0,4783	2,70	0,4965	3,95	0,49996
1,68	0,4535	2,04	0,4793	2,72	0,4967	4,00	0,499968
1,69	0,4545	2,06	0,4803	2,74	0,4969	4,50	0,499997
1,70	0,4554	2,08	0,4812	2,76	0,4971	5,00	0,499997
1,71	0,4564	2,10	0,4821	2,78	0,4973	>5	0,5
1,72	0,4573	2,12	0,4830	2,80	0,4974
1,73	0,4582	2,14	0,4838	2,82	0,4976