Указания к выполнению контрольных заданий 1 страница
Вопросы для подготовки к зачету по дисциплине
«Эконометрика»
1. Эконометрика и экономическая теория. Эконометрика и статистика. Эконометрика и экономико-математические методы.
2. Эконометрические модели: общая характеристика. Области применения эконометрических моделей.
- Понятие о функциональной, статистической и корреляционной связях. Основные задачи прикладного корреляционно-регрессионного анализа.
- Уравнение регрессии, его смысл и назначение. Выбор типа математической функции при построении уравнения регрессии.
- Парная регрессия. Метод наименьших квадратов и условия его применения для определения параметров уравнения парной регрессии.
- Оценка степени тесноты связи между количественными переменными. Показатели корреляции: линейный коэффициент корреляции, индекс корреляции, теоретическое корреляционное отношение. Коэффициент детерминации.
- Стандартная ошибка уравнения регрессии.
8. Оценка статистической значимости показателей корреляции, параметров уравнения регрессии, уравнения регрессии в целом: t - критерий Стьюдента, F - критерий Фишера.
9. Понятие о множественной регрессии. Классическая линейная модель множественной регрессии (КЛММР). Определение параметров уравнения множественной регрессии методом наименьших квадратов.
10. Стандартизованные коэффициенты регрессии, их интерпретация.
11. Парные и частные коэффициенты корреляции.
12. Множественный коэффициент корреляции и множественный коэффициент детерминации. Оценка надежности показателей корреляции.
13. Оценка качества модели множественной регрессии: F – критерий Фишера, t - критерий Стьюдента.
14. Мультиколлинеарность. Методы выявления и устранения мультиколлинеарности.
15. Фиктивные переменные в регрессионных моделях. Модели ANOVA и ANCOVA.
16. Спецификация переменных в уравнениях регрессии. Ошибки спецификации.
17. Проблема выявления гетероскедастичности в регрессионных моделях.
18. Специфика временных рядов как источника данных в эконометрическом моделировании.
19. Аналитическое выравнивание временных рядов. Оценка параметров уравнения тренда.
20. Автокорреляция уровней временного ряда ее измерение и последствия.
21.Автокорреляция в остатках, ее измерение и последствия. Критерий Дарбина- Уотсона.
22.Модели авторегрессии.
Методические указания по выполнению контрольной работы
Контрольная работа по дисциплине “Эконометрика”
Общие указания по выполнению контрольной работы
Задания к контрольной работе составлены в 10 вариантах. Номер варианта соответствует последней цифре шифра зачетной книжки.Если последняя цифра зачетной книжки – 0, следует выполнить 10-й вариант.
Каждый вариант контрольной работы содержит 4 задачи по основным разделам курса. Порядковый номер задачи из каждой темы соответствует номеру варианта.
1. Результаты расчетов всех относительных величин необходимо проводить с точностью до 0,0001, а процентов - до 0,01.
2. Все расчеты могут быть выполнены как вручную, так и с использованием пакетов прикладных программ на персональном компьютере. В последнем случае следует обязательно указывать название и версию использованного программного обеспечения. Соответствующие распечатки необходимо привести в тексте работы или оформить в качестве приложения.
3. Все расчеты должны сопровождаться комментариями и интерпретацией полученных результатов.
Указания к выполнению контрольных работ содержат все необходимые формулы, а также содержат примеры расчетов типовых задач, которые по тексту указаний выделены курсивом.
Указания к выполнению контрольных заданий
Задача 1по теме “Парная регрессия и корреляция”.
Введем следующие обозначения:
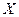- факторный признак, независимая (объясняющая) переменная,
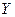- результативный признак, зависимая переменная,
x – фактические значения факторного признака,
y – фактические значения результативного признака,
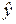- расчетные (полученные по уравнению регрессии) значения результативного признака,
a , b - параметры уравнения регрессии.
В контрольных заданиях используется уравнение парной линейной регрессии вида:
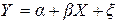
Рассмотрим методику выполнения на условиях конкретной задачи:
American Express Company в течение долгого времени полагала, что владельцы ее кредитных карт предпочитают оплачивать свои расходы во время путешествий при помощи их карт. Для выяснения этого из компьютерной базы компании были случайно выбраны 25 владельцев карточек, которым были заданы вопросы о числе миль, которые они провели в путешествиях. Данные опроса о расходах путешественников и числе миль, проведенных ими в пути, составляют исходную информацию задачи.
| N п/п | Число миль, проведенных в пути, X | Расходы, у.е , Y | N п/п | Число миль, проведенных в пути, X | Расходы, у.е , Y |
| 1 | 1211 | 1802 | 14 | 3209 | 4492 |
| 2 | 1345 | 2405 | 15 | 3466 | 4244 |
| 3 | 1422 | 2005 | 16 | 3643 | 5298 |
| 4 | 1687 | 2511 | 17 | 3852 | 4801 |
| 5 | 1847 | 2332 | 18 | 4033 | 5147 |
| 6 | 2026 | 2305 | 19 | 4267 | 5738 |
| 7 | 2133 | 3016 | 20 | 4498 | 6420 |
| 8 | 2253 | 3385 | 21 | 4533 | 6059 |
| 9 | 2400 | 3090 | 22 | 4804 | 6426 |
| 10 | 2468 | 3694 | 23 | 5090 | 6321 |
| 11 | 2699 | 3371 | 24 | 5233 | 7025 |
| 12 | 2806 | 3998 | 25 | 5439 | 6964 |
| 13 | 3082 | 3555 |
Пункт 1. Построение поля корреляции результата и фактора производится по исходным данным о парах значений факторного и результативного признаков с соблюдением масштаба. На основе поля корреляции делаются выводы о направлении и возможной функциональной форме связи между факторным и результативным признаками (прямая - обратная, линейная - нелинейная).
 |
Для условий рассматриваемой задачи поле корреляции выглядит следующим образом:
Связь между факторным и результативным признаками прямая, линейная.
Пункт 2. Оценка параметров уравнения парной линейной регрессии производится обычным методом наименьших квадратов (МНК):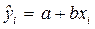 
, где
a и b –оценки параметров модели.
Величины, минимизирующие суммы квадратов отклонений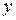 
от 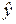для случая парной линейной регрессии, находятся как:
;
.
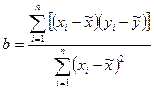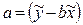Значения ошибок, называемые обычно остатками, рассчитываются как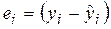 
.
Проведите интерпретацию полученных результатов.
Расчет необходимых данных лучше всего организовать в таблице. Для нашего примера таблица будет выглядеть следующим образом:
Таблица 1
| N/N | х | у |  |  |  |  |  |  |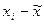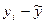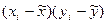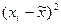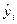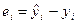
| -1966,84 | -2454,16 | 1787,652 | 14,34756 | |||||
| -1832,84 | -1851,16 | 1955,831 | 449,1692 | |||||
| -1755,84 | -2251,16 | 2052,471 | -47,4707 | |||||
| -1490,84 | -1745,16 | 2385,062 | 125,9377 | |||||
| -1330,84 | -1924,16 | 2585,872 | -253,872 | |||||
| -1151,84 | -1951,16 | 2810,529 | -505,529 | |||||
| -1044,84 | -1240,16 | 2944,82 | 71,17973 | |||||
| -924,84 | -871,16 | 805683,6 | 3095,428 | 289,5722 | ||||
| -777,84 | -1166,16 | 907085,9 | 605035,1 | 3279,922 | -189,922 | |||
| -709,84 | -562,16 | 399043,7 | 503872,8 | 3365,266 | 328,7337 | |||
| -478,84 | -885,16 | 229287,7 | 3655,186 | -284,186 | ||||
| -371,84 | -258,16 | 95994,21 | 3789,477 | 208,5225 | ||||
| -95,84 | -701,16 | 67199,17 | 9185,306 | 4135,875 | -580,875 | |||
| Продолжение таблицы 1 | ||||||||
| N/N | х | у | | | | | | |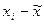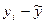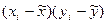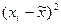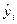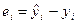
| 31,16 | 235,84 | 7348,774 | 970,9456 | 4295,268 | 196,7322 | |||
| 288,16 | -12,16 | -3504,03 | 83036,19 | 4617,819 | -373,819 | |||
| 465,16 | 1041,84 | 484622,3 | 216373,8 | 4839,965 | 458,035 | |||
| 674,16 | 544,84 | 367309,3 | 454491,7 | 5102,273 | -301,273 | |||
| 855,16 | 890,84 | 761810,7 | 731298,6 | 5329,439 | -182,439 | |||
| 1089,16 | 1481,84 | 5623,124 | 114,8759 | |||||
| 1320,16 | 2163,84 | 5913,044 | 506,9564 | |||||
| 1355,16 | 1802,84 | 5956,971 | 102,0292 | |||||
| 1626,16 | 2169,84 | 6297,093 | 128,9072 | |||||
| 1912,16 | 2064,84 | 6656,041 | -335,041 | |||||
| 2055,16 | 2768,84 | 6835,515 | 189,4853 | |||||
| 2261,16 | 2707,84 | 7094,058 | -130,058 | |||||
| сумма | ||||||||
| Средн. | 3177,84 | 4256,16 |
В соответствии с расчетами, представленными в таблице 1, а= 267,7715; b=1,2551
Соответственно уравнение регрессии может быть записано как:
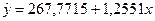
Коэффициент регрессии линейной функции (b) есть абсолютный показатель силы связи, характеризующий среднее абсолютное изменение результата при изменении факторного признака на единицу своего измерения.
Полученное уравнение может быть объяснено следующим образом: с увеличением расстояния на 1 милю расходы путешественника в среднем увеличиваются на 1,2551 условных денежных единиц. Свободный член уравнения равен 267,7715, что может трактоваться как влияние на величину расходов других, неучтенных в модели факторов.
Пункт 3. Линейный коэффициент корреляции характеризует тесноту линейной связи между изучаемыми признаками. Его можно определить по следующей формуле: 
.
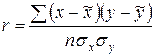Значения линейного коэффициента корреляции принадлежит промежутку [-1;1].
Чем ближе его абсолютное значение к 1, тем теснее связь между признаками. Положительная величина свидетельствует о прямой связи между изучаемыми признаками, отрицательная - о наличии обратной связи между признаками.
Для нашей задачи r=0,98329, что подтверждает вывод, сделанный в пункте 1, что связь между признаками прямая, а также указывает на очень сильную взаимосвязь между количеством миль, проведенных в пути и расходами.
Квадрат коэффициента (индекса) корреляции называется коэффициентом детерминации и показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах. Например: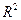 
=0,8 означает, что доля колеблемости результативного признака, объясненная вариацией фактора 
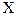, включенного в уравнение регрессии, равна 80%. Остальные 20% приходятся на долю прочих факторов, не учтенных в уравнении регрессии.
Для нашей задачи коэффициент детерминации равен 0,9669, то есть 96,69% вариации результативного признака (расходов путешественников) объясняется вариацией факторного признака (количеством миль, проведенных в пути)
Пункт 4 связан с темой “Проверка статистических гипотез”. Рекомендуется использовать следующую общую процедуру проверки гипотез:
1.Сформулируйте нулевую гипотезу о том, что коэффициент регрессии статистически незначим: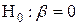 
(линейной зависимости нет)
при конкурирующей: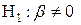 
(линейная зависимость есть)
или о том, что уравнение в целом статистически незначимо: 
.
2.Определите фактическое значение соответствующего критерия.
3.Сравните полученное фактическое значение с табличным.
4.Если фактическое значение используемого критерия превышает табличное, нулевая гипотеза отклоняется, и с вероятностью (1-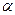 
) принимается альтернативная гипотеза о статистической значимости коэффициента регрессии. Если фактическое значение t - критерия меньше табличного, оснований отклонять нулевую гипотезу - нет.
Статистическая значимость коэффициента регрессии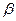 
проверяется с помощью t - критерия Стьюдента:
,
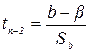где
,
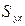- стандартная ошибка оценки, рассчитываемая по формуле
.
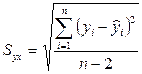Так как нулевая гипотеза предполагает, что 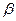=0, то tнабл. рассчитывается как:
.
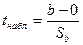Для определения табличного значения воспользуйтесь таблицами распределения Стьюдента для заданного уровня значимости α, принимая во внимание, что число степеней свободы для распределения Стьюдента равно (k = n - 2).
Для нашего примера 
, а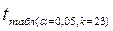 
=2,07, следовательно нулевая гипотеза отвергается в пользу альтернативной и коэффициент регрессии 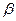статистически значим, то есть наличие существенной линейной зависимости между количеством миль, проведенных в путешествии и величиной расходов статистически подтверждается.
Оценка статистической значимости построенной модели регрессии в целом производится с помощью F- критерия Фишера. Фактическое значение F-критерия качества оценивания регрессии, который представляет собой отношение объясненной суммы квадратов SSR (в расчете на одну независимую переменную) к остаточной сумме квадратов SSE (в расчете на одну степень свободы), определяется как:
,
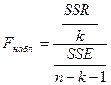где SSR = 
- факторная, или объясненная моделью регрессии, сумма квадратов,
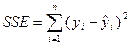- остаточная, или необъясненная моделью сумма квадратов
k - число независимых переменных.
F - критерий можно выразить через коэффициент детерминации:
.
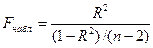Для определения табличного значения воспользуйтесь таблицами распределения Фишера-Снедекора для заданного уровня значимости α, принимая во внимание, что в случае парной регрессии число степеней свободы большей дисперсии равно 1, а число степеней свободы меньшей дисперсии равно n - 2.
Для нашего примера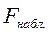 
=671, 137, а 
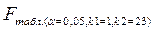=4,45. Так как 
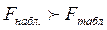построенная модель регрессии в целом значима и может в дальнейшем использоваться нами для прогнозов.
Для выполнения пункта 5 необходимо изучить вопрос об интервальном оценивании в регрессионном анализе, уяснить смысл понятий “точечный прогноз” и “интервальный прогноз”. Для расчета точечного прогноза 
подставьте в уравнение регрессии заданное значение факторного признака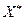 
.
Так, например, если необходимо оценить расходы путешественника, преодолевшего (собирающегося преодолеть) 4500 миль, следует использовать уравнение регрессии записанное нами в пункте 2:
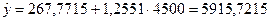, то есть в среднем путешественник, преодолевший 4500 миль израсходует 5915,7215 условных денежных единиц.
Доверительный интервал для значений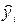 
, лежащих на линии регрессии, имеет вид:
,
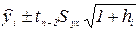где
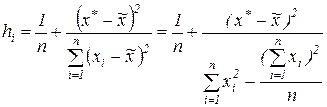
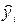- прогнозное значение зависимой переменной;
- стандартная ошибка оценки;
n - объем выборки;
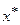- заданное значение 
.
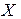Полученный интервал будет характеризовать значения результативного признака при заданном значении факторного признака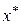 
для отдельной наблюдаемой единицы.
Так, для нашего примера этот доверительный интервал будет выглядеть как 5247,8367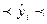 
6582,9665, то есть с вероятностью 0,95 можно утверждать, что расходы одного путешественника, преодолевшего 4500 миль составят от 5247,8367 до 6582,9665 условных денежных единиц.
Если же необходимо сделать вывод об интервале значений результативного признака для всех наблюдаемых единиц при среднем значении факторного признака 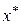, расчет будет производиться по формуле доверительного интервала генерального значения 
:
.
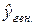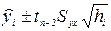В соответствии с условиями рассматриваемого примера доверительный интервал, характеризующий расходы всех путешественников, преодолевших 4500 миль будет выглядеть как 5730,918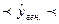 
6099,885, то есть расходы всехпутешественников, преодолевших расстояние в 4500 миль составят от 5730,918 до 6099,885 условных денежных единиц.
Сделайте выводы по задаче в целом.
Задача 2 по теме “Множественная регрессия и корреляция”.
Задача предполагает построение и анализ двухфакторного уравнения линейной регрессии вида:
.
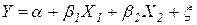Рассмотрим методику решения задачи такого типа на примере:
Компания, производящая моющие средства, предприняла рекламную акцию в магазинах с демонстрацией антисептических свойств нового моющего средства. В этот же период компания использовала обычную теле- и радиорекламу. Через 20 недель компания решила проанализировать сравнительную эффективность различных видов рекламных расходов. Аналитик компании, исходя из гипотезы о линейной регрессионной взаимосвязи, оценил параметры модели следующего вида:
,
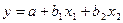где
– объем продаж моющего средства,
– расходы на теле и радио рекламу,
– расходы на демонстрацию товара в магазинах.
Расходы приведены в условных денежных единицах.
Таблица 1. Исходные данные
| Номера наблюдений | | | |
| 1 | 72 | 12 | 5 |
| 2 | 76 | 11 | 7 |
| 3 | 78 | 15 | 6 |
| 4 | 70 | 10 | 5 |
| 5 | 68 | 11 | 3 |
| 6 | 80 | 16 | 7 |
| 7 | 82 | 14 | 3 |
| 8 | 65 | 8 | 4 |
| 9 | 62 | 8 | 3 |
| 10 | 90 | 18 | 5 |
Пункт 1 посвящен анализу показателей тесноты связи в уравнении множественной регрессии.
Но прежде чем приступить к анализу показателей тесноты связи необходимо рассмотреть дискриптивные (описательные статистики), которые подробно изучались в курсах математической статистики с элементами теории вероятностей и общей теории статистики
Таблица 2. Дискриптивные статистики