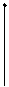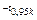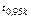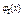Опр. Статистической гипотезой наз-ся любое предположение о виде или параметре неизвестного закона распред-я. Обычно проверяемую гипотезу обозначают через Но.;
Пусть дан вариационный ряд.
| возмож-ые знач. признака Х | Х1 | Х2 | … | Хк | å |
| число объектов | n1 | n2 | … | nk | n |
Гипотеза Но: {Обязательно формулировать при задачах} Случайная величина Х-з/п рабочего имеет нормальный закон распред-я с параметрами а=151,6; s=24,3 (отклонение эксперем-х данных от теорет-х вызвано случ-ми факторами). Экспериментальные данные ni- эмпирические частоты (см. вар. ряд). (i=1,2,…m, где m- число
тнтервалов). Теоретич-ие данные (см. гипотезу Но);
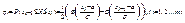 ;
; 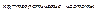 .
.
В качестве меры расхождения между эксперим-ми и теорит-ми данными испол-ют статистику 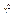 (хи).
(хи). 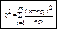 Статистика – случайная вел. с парам.; При
Статистика – случайная вел. с парам.; При
достаточно большом n закон распределения статистики 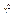 известен и не зависит от
известен и не зависит от
закона распред-я случ. величины Х. При nॠэта статистика имеет так называемое 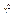 распределение с K=m-S-1 степенями свободы. (m-число интервалов; S- число параметров закона распр-я Х).; Опр.: Уравнением значимости наз-ся вер-ть отвергнуть гипотезу Но, когда она верна. a- ур-нь значимости (тоже что и эпсило). Опр.:
распределение с K=m-S-1 степенями свободы. (m-число интервалов; S- число параметров закона распр-я Х).; Опр.: Уравнением значимости наз-ся вер-ть отвергнуть гипотезу Но, когда она верна. a- ур-нь значимости (тоже что и эпсило). Опр.:
Пороговым значением 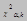 - наз-ся число, определ-ое равенством
- наз-ся число, определ-ое равенством 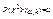 . Опр.: Правило по которому гипотеза Но приним-ся или отвергается наз-ся статистическим критерием.
. Опр.: Правило по которому гипотеза Но приним-ся или отвергается наз-ся статистическим критерием.
Критерий Пирсона:Если вычисл-оезначение статистики 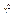 меньше порогового значения
меньше порогового значения 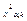 ,то гипотеза Но приним-ся, в противном случае отвеграется на ур-не значимости a. Замечание: Отвержение гипотезы Но, когда она верна – ошибка 1-го рода. Наоборот вер-ть принять гипотезу h когда она не верна –ошибка 2-рода.
,то гипотеза Но приним-ся, в противном случае отвеграется на ур-не значимости a. Замечание: Отвержение гипотезы Но, когда она верна – ошибка 1-го рода. Наоборот вер-ть принять гипотезу h когда она не верна –ошибка 2-рода.
Коэффициент корреляции и его св-ва (продолжение). 1)Пусть r- коэфф-нт корреляции случ. Величин X и Y 
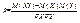 . Заменяя в последнем
. Заменяя в последнем
выражении входящие величины на их выборочные оценки, получаем формулу вычисления выборочного коэфф-нта корреляции r: 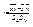 , где
, где 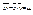 -выборочная ковариация.; Известно
-выборочная ковариация.; Известно 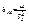 ;
; 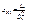
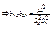 ;
; 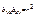 . Т.к. знаки коэфф-та коррел-ции r с одной стороны и коэфф-тов прямых регрессий
. Т.к. знаки коэфф-та коррел-ции r с одной стороны и коэфф-тов прямых регрессий
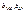 совпадают (определяются знаки m), то справедлива формула:
совпадают (определяются знаки m), то справедлива формула: 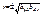 , где зн. «+»- в случае
, где зн. «+»- в случае 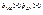 , зн. «-»- если
, зн. «-»- если 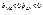 . Опр.: Если r>0, то связь между переменными наз-ся прямой. Если r<0- связь обратная. Опр. Связь между переменными тесная, если |r|³0,7;умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции |r|£1.
. Опр.: Если r>0, то связь между переменными наз-ся прямой. Если r<0- связь обратная. Опр. Связь между переменными тесная, если |r|³0,7;умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции |r|£1.
Предельное значение коэфф-та корреляции.
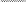
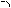


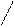
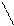


Пусть|r|=1 т.ит.т.к.
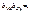
по геометрическому смыслу коэфф-нт прямых регрессий
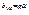
, а
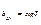



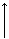
tga×ctgb=1; tga×1/tgb=1; tga=tgb=>прямые регрессии
паралельны, но т.к. он имеютобщую точку ( 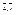 ), то прямые регрессии совпадают. Вывод: при |r|=1 прямые
), то прямые регрессии совпадают. Вывод: при |r|=1 прямые
регрессии совпадают.2)r=0ó т.ит.т.к. m=0 т.ит.т.к. 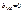 и
и
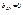 ;
; 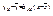 ;
;
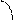

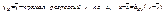
;
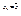
-прямая регрессий х по у.; Замечание: Если r=0, то говорят,
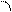


что между переменными х и у отсутствуеет линейная зависимость. Дополнение: Ур-ия прямых регрессий имеют вид:
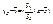 ,
, 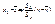 ,
, 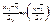 ,
, 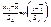 .
.
Обозначим 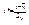 ,
, 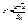 , в терминах эти ур-ния прямых
, в терминах эти ур-ния прямых
регрессий имеют вид:
tga=r, ctgb=r;
tga=tg(a-b)= 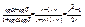 ; tgj=
; tgj= 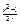 .
.
Оценка значимости коэфф-та корреляции. Рассмотрим следующую гипотезу Но: коэфф-нт корреляции=0, т.е r=0. В кач-ве меры доверия к справедливости данной гипотезы исп-ся статистика. 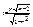 . Закон распр-я данной статистики известен: она имеет так называемые распредел-е Стьюдента с k=n-2 степенями свободы.; Опр. Пороговое значение
. Закон распр-я данной статистики известен: она имеет так называемые распредел-е Стьюдента с k=n-2 степенями свободы.; Опр. Пороговое значение 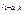 , для статистики t определяется равенством
, для статистики t определяется равенством 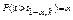 .;
.;
Критерий Стьюдента: Если вычисленное значение статистики t удовлетворяет нер-ву 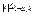 - гипотеза n-Ho принимается, в противном случае – отвергается на уровне
- гипотеза n-Ho принимается, в противном случае – отвергается на уровне
значимости a.





t попадает в эту область с вер-тью 0,95
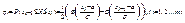 ;
; 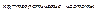 .
.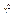 (хи).
(хи). 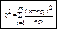 Статистика – случайная вел. с парам.; При
Статистика – случайная вел. с парам.; При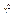 известен и не зависит от
известен и не зависит от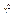 распределение с K=m-S-1 степенями свободы. (m-число интервалов; S- число параметров закона распр-я Х).; Опр.: Уравнением значимости наз-ся вер-ть отвергнуть гипотезу Но, когда она верна. a- ур-нь значимости (тоже что и эпсило). Опр.:
распределение с K=m-S-1 степенями свободы. (m-число интервалов; S- число параметров закона распр-я Х).; Опр.: Уравнением значимости наз-ся вер-ть отвергнуть гипотезу Но, когда она верна. a- ур-нь значимости (тоже что и эпсило). Опр.: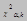 - наз-ся число, определ-ое равенством
- наз-ся число, определ-ое равенством 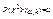 . Опр.: Правило по которому гипотеза Но приним-ся или отвергается наз-ся статистическим критерием.
. Опр.: Правило по которому гипотеза Но приним-ся или отвергается наз-ся статистическим критерием.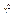 меньше порогового значения
меньше порогового значения 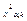 ,то гипотеза Но приним-ся, в противном случае отвеграется на ур-не значимости a. Замечание: Отвержение гипотезы Но, когда она верна – ошибка 1-го рода. Наоборот вер-ть принять гипотезу h когда она не верна –ошибка 2-рода.
,то гипотеза Но приним-ся, в противном случае отвеграется на ур-не значимости a. Замечание: Отвержение гипотезы Но, когда она верна – ошибка 1-го рода. Наоборот вер-ть принять гипотезу h когда она не верна –ошибка 2-рода.
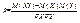 . Заменяя в последнем
. Заменяя в последнем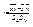 , где
, где 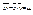 -выборочная ковариация.; Известно
-выборочная ковариация.; Известно 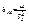 ;
; 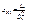
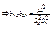 ;
; 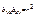 . Т.к. знаки коэфф-та коррел-ции r с одной стороны и коэфф-тов прямых регрессий
. Т.к. знаки коэфф-та коррел-ции r с одной стороны и коэфф-тов прямых регрессий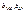 совпадают (определяются знаки m), то справедлива формула:
совпадают (определяются знаки m), то справедлива формула: 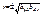 , где зн. «+»- в случае
, где зн. «+»- в случае 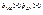 , зн. «-»- если
, зн. «-»- если 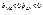 . Опр.: Если r>0, то связь между переменными наз-ся прямой. Если r<0- связь обратная. Опр. Связь между переменными тесная, если |r|³0,7;умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции |r|£1.
. Опр.: Если r>0, то связь между переменными наз-ся прямой. Если r<0- связь обратная. Опр. Связь между переменными тесная, если |r|³0,7;умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции |r|£1.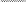
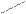
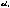
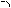


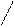
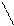

 Пусть|r|=1 т.ит.т.к.
Пусть|r|=1 т.ит.т.к. 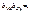 по геометрическому смыслу коэфф-нт прямых регрессий
по геометрическому смыслу коэфф-нт прямых регрессий 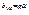 , а
, а 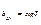



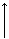 tga×ctgb=1; tga×1/tgb=1; tga=tgb=>прямые регрессии
tga×ctgb=1; tga×1/tgb=1; tga=tgb=>прямые регрессии 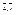 ), то прямые регрессии совпадают. Вывод: при |r|=1 прямые
), то прямые регрессии совпадают. Вывод: при |r|=1 прямые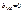 и
и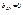 ;
; 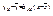 ;
;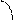

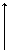
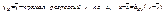 ;
; 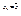 -прямая регрессий х по у.; Замечание: Если r=0, то говорят,
-прямая регрессий х по у.; Замечание: Если r=0, то говорят, 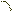
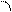

 что между переменными х и у отсутствуеет линейная зависимость. Дополнение: Ур-ия прямых регрессий имеют вид:
что между переменными х и у отсутствуеет линейная зависимость. Дополнение: Ур-ия прямых регрессий имеют вид: 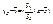 ,
, 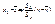 ,
, 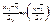 ,
, 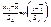 .
.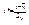 ,
, 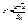 , в терминах эти ур-ния прямых
, в терминах эти ур-ния прямых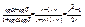 ; tgj=
; tgj= 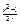 .
.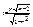 . Закон распр-я данной статистики известен: она имеет так называемые распредел-е Стьюдента с k=n-2 степенями свободы.; Опр. Пороговое значение
. Закон распр-я данной статистики известен: она имеет так называемые распредел-е Стьюдента с k=n-2 степенями свободы.; Опр. Пороговое значение 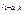 , для статистики t определяется равенством
, для статистики t определяется равенством 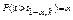 .;
.;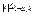 - гипотеза n-Ho принимается, в противном случае – отвергается на уровне
- гипотеза n-Ho принимается, в противном случае – отвергается на уровне