Направление выпуклости графика функции. Точки перегиба
Определение: Кривая  называется выпуклой вниз в промежутке
называется выпуклой вниз в промежутке  , если она лежит выше касательной в любой точке этого промежутка.
, если она лежит выше касательной в любой точке этого промежутка.
Определение: Кривая  называется выпуклой вверх в промежутке
называется выпуклой вверх в промежутке  , если она лежит ниже касательной в любой точке этого промежутка.
, если она лежит ниже касательной в любой точке этого промежутка.

 y y
y y
x x
Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции  , характеризуется знаком ее второй производной: если в некотором промежутке
, характеризуется знаком ее второй производной: если в некотором промежутке  , то кривая выпукла вниз на этом промежутке; если же
, то кривая выпукла вниз на этом промежутке; если же  , то кривая выпукла вверх на этом промежутке.
, то кривая выпукла вверх на этом промежутке.
Определение: Точка графика функции  , разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
, разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции  , в которых вторая производная
, в которых вторая производная  обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
6.7. Правило нахождения точек перегиба графика функции 
1. Найти вторую производную  .
.
2. Найти критические точки II рода функции  , т.е. точки, в которой
, т.е. точки, в которой  обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
3. Исследовать знак второй производной  в промежутках, на которые найденные критические точки делят область определения функции
в промежутках, на которые найденные критические точки делят область определения функции  . Если при этом критическая точка
. Если при этом критическая точка  разделяет промежутки выпуклости противоположных направлений, то
разделяет промежутки выпуклости противоположных направлений, то  является абсциссой точки перегиба графика функции.
является абсциссой точки перегиба графика функции.
4. Вычислить значения функции в точках перегиба.
Пример 1: Найти промежутки выпуклости и точки перегиба следующей кривой:  .
.
Решение: Находим  ,
,  .
.
Найдем критические точки по второй производной, решив уравнение  .
.
 .
.
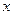 |  |  | |
 | + | - | |
 |  | точка перегиба |  |

Ответ: Функция выпукла вверх при  ;
;
функция выпукла вниз при  ;
;
точка перегиба  .
.
Асимптоты.
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.
Определение. Прямая называется асимптотойкривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции  . Ее наклонная асимптота у = х.
. Ее наклонная асимптота у = х.

Рассмотрим подробнее методы нахождения асимптот кривых.
