Понятие дифференцируемости функции в точке. Необходимое и достаточное условие дифференцируемости в точке
Понятие дифференцируемости функции
Пусть функция 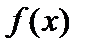 определена в точке
определена в точке 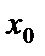 и некоторой ее окрестности. Обозначим символом
и некоторой ее окрестности. Обозначим символом 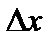 любое приращение аргумента, такое, что
любое приращение аргумента, такое, что 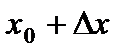 принадлежит указанной окрестности точки
принадлежит указанной окрестности точки 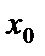 .
.
Определение. Функция 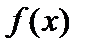 называется дифференцируемой в точке
называется дифференцируемой в точке 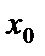 , если приращение
, если приращение 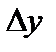 этой функции в точке
этой функции в точке 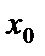 , соответствующее приращению аргумента
, соответствующее приращению аргумента 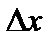 , может быть представлено в виде
, может быть представлено в виде
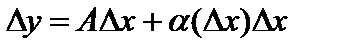 , (1)
, (1)
где 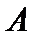 — некоторое число, не зависящее от
— некоторое число, не зависящее от 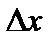 ,
, 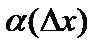 — бесконечно малая функция при
— бесконечно малая функция при 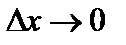 .
.
Заметим, что поскольку 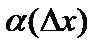 — бесконечно малая функция, то
— бесконечно малая функция, то 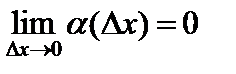 . Тогда
. Тогда 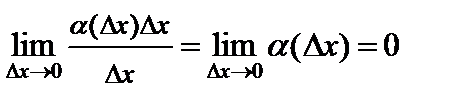 . Следовательно,
. Следовательно, 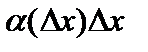 является бесконечно малой более высокого порядка, чем
является бесконечно малой более высокого порядка, чем 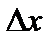 , и обозначается
, и обозначается 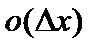 . Учитывая это обозначение, формулу (3) можно также записать в виде
. Учитывая это обозначение, формулу (3) можно также записать в виде
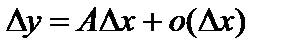 , (2)
, (2)
Теорема. Для того чтобы функция 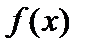 была дифференцируемой в точке
была дифференцируемой в точке 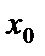 , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство необходимости. Пусть функция 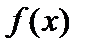 дифференцируема в точке
дифференцируема в точке 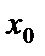 , то есть ее приращение представимо в виде (1). Разделим равенство (1) на
, то есть ее приращение представимо в виде (1). Разделим равенство (1) на 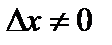 и перейдем к пределу при
и перейдем к пределу при 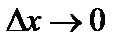 . В результате получим
. В результате получим
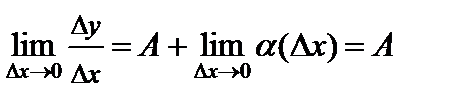 .
.
Отсюда следует, что в точке 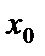 существует конечная производная
существует конечная производная 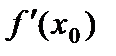 , равная
, равная 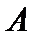 .
.
Доказательство достаточности. Пусть функция 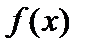 имеет в точке
имеет в точке 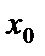 конечную производную, то есть существует предельное значение
конечную производную, то есть существует предельное значение
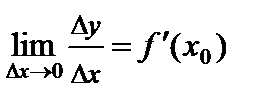 .
.
В силу определения предельного значения, разность 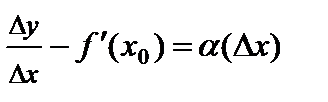 , где
, где 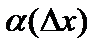 — бесконечно малая функция при
— бесконечно малая функция при 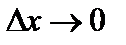 . Отсюда имеем
. Отсюда имеем
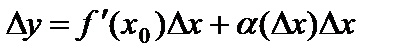 . (3)
. (3)
Данное представление приращения функции совпадает с представлением (1), если обозначить через 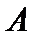 не зависящее от
не зависящее от 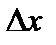 число
число 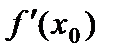 . Следовательно, функция
. Следовательно, функция 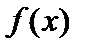 является дифференцируемой в точке
является дифференцируемой в точке 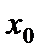 .
.
Правила дифференцирования также были сформулированы в предыдущей лекции. Докажем теперь некоторые из них.
1. Пусть функция 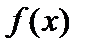 имеет производную в данной точке
имеет производную в данной точке 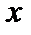 . Тогда функция
. Тогда функция 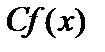 , где
, где 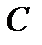 — постоянная, также имеет в этой точке производную, причем
— постоянная, также имеет в этой точке производную, причем 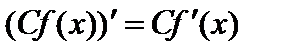 .
.
Рассмотрим функцию 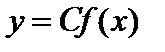 . Найдем приращение этой функции в данной точке
. Найдем приращение этой функции в данной точке 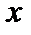 , соответствующее приращению аргумента
, соответствующее приращению аргумента 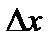
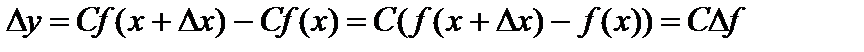 .
.
По определению производной имеем
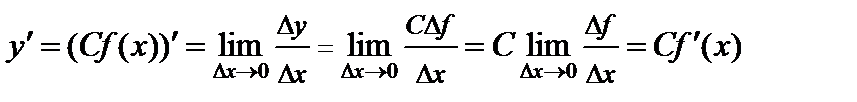 .
.
2. Пусть функции 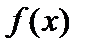 и
и 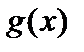 имеют производные в данной точке
имеют производные в данной точке 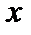 . Тогда сумма и разность этих функций также имеют в этой точке производные, причем
. Тогда сумма и разность этих функций также имеют в этой точке производные, причем
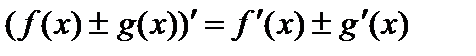 .
.
Пусть 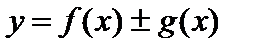 . Тогда
. Тогда
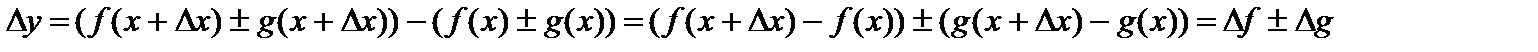 ,
,
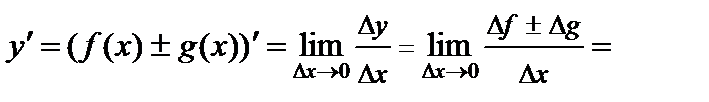
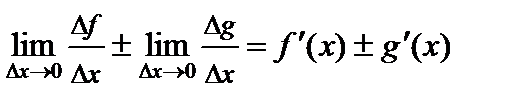 .
.
3. Пусть функции 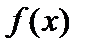 и
и 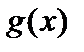 имеют производные в данной точке
имеют производные в данной точке 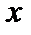 . Тогда произведение этих функций также имеет в этой точке производную, причем
. Тогда произведение этих функций также имеет в этой точке производную, причем 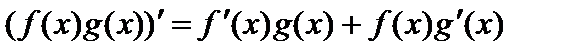 .
.
Обозначим 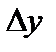 ,
, 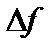 и
и 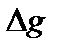 приращения функций
приращения функций 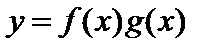 ,
, 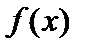 и
и 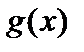 в точке
в точке 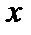 , соответствующие приращению аргумента
, соответствующие приращению аргумента 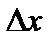 . Заметив, что
. Заметив, что 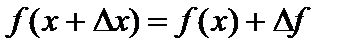 ,
, 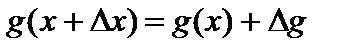 , найдем приращение
, найдем приращение 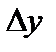
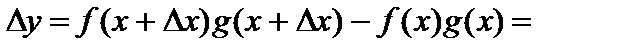
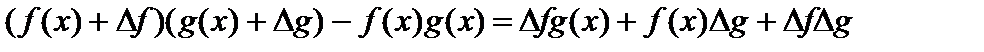 .
.
Так как функции 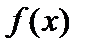 и
и 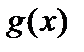 имеют производную в точке
имеют производную в точке 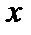 , то они непрерывны в этой точке. Следовательно,
, то они непрерывны в этой точке. Следовательно, 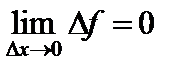 и
и 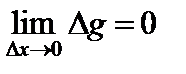 . Учитывая эти равенства и определение производной, получим
. Учитывая эти равенства и определение производной, получим
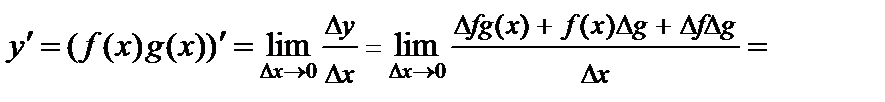
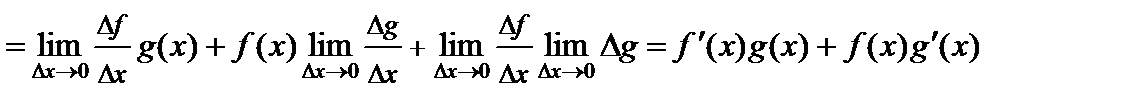 .
.
4. Пусть функции 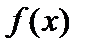 и
и 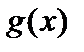 имеют производные в данной точке
имеют производные в данной точке 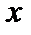 . Тогда частное этих функций при условии, что
. Тогда частное этих функций при условии, что 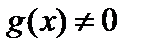 , также имеет в этой точке производную, причем
, также имеет в этой точке производную, причем 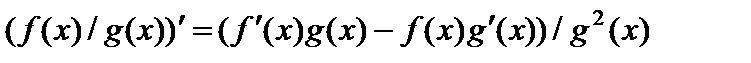 .
.
Правило дифференцирования частного доказывается аналогично предыдущим.
Таблица производных.
Таблица производных простейших элементарных функций
1. 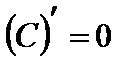 , где
, где 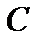 — постоянная;
— постоянная;
2. 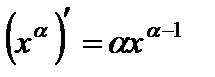 ,
, 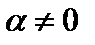 ;
;
3. 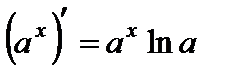 ,
, 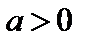 ;
;
4. 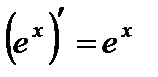 ;
;
5. 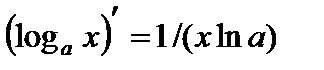 ,
, 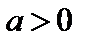 ,
, 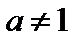 ;
;
6. 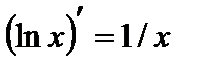 ;
;
7. 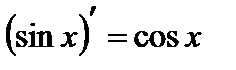 ;
;
8. 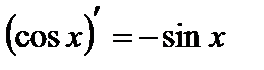 ;
;
9. 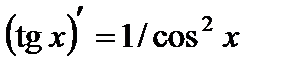 ;
;
10. 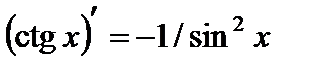 ;
;
11. 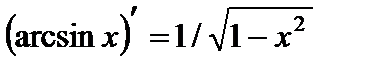 ;
;
12. 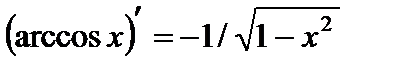 ;
;
13. 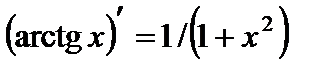 ;
;
14. 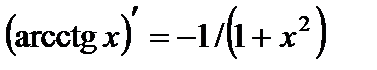 .
.
