Третий признак равенства треугольников

Третий признак равенства треугольников по трем сторонам формулируется в виде теоремы.

Теорема: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

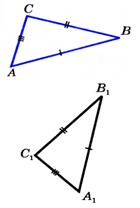Доказательство. рассмотримΔABC и ΔA₁B₁C₁ у которых AB=A₁B₁, AC=A₁C₁, ВС=В₁С₁. Докажем, что ΔABC=ΔA₁B₁C₁

Пусть ABC и A₁B₁C₁ – треугольники, у которых AB=A₁B₁, AC=A₁C₁, BC=B₁C₁. Наложим ∆ABC на ∆A₁B₁C₁ так, чтобы вершина A совместиласьA₁, а вершины B и B₁, а вершины С и С₁ оказались по разные стороны от прямой A₁В₁. Возможны три случая: 1) луч С₁С проходит внутри угла А₁С₁В₁ (рис. а)); 2)луч С₁С совпадает с одной из сторон этого угла (рис. б)); луч С₁С проходит вне угла А₁С₁В₁ (рис. в)). Рассмотрим первый случай. Так как по условию теоремы стороны АС и A₁C₁, ВС и В₁С₁ равны, то треугольники А₁С₁С и В₁С₁С — равнобедренные. По теореме о свойстве углов равнобедренного треугольника Ðl = Ð2, Ð3 = Ð4, поэтому ÐA₁CB₁ = =ÐA₁С₁B₁. Итак, AC=A₁C₁, BC=B₁C₁, ÐС = ÐС₁. Следовательно, треугольники ABC и А₁В₁С₁ равны по первому признаку равенства треугольников.

Запись на доске:

Дано: ΔABC, ΔA₁B₁C₁, AB=A₁B₁, AC=A₁C₁, ВС=В₁С₁

Доказать: ΔABC=ΔA₁B₁C₁

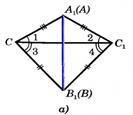
Доказательство. Наложим ∆ABC на ∆A₁B₁C₁ так, чтобы A →A₁, а B → B₁, а С и С₁ оказались по разные стороны от прямой A₁В₁. Рассмотрим случай. луч С₁С проходит внутри ÐА₁С₁В₁ (рис. а)).

АС=A₁C₁, ВС=В₁С₁ ═> ΔА₁С₁С и ΔВ₁С₁С — равноб. ═> Ðl = Ð2, Ð3 = Ð4 (по св-ву углов равноб. Δ), ═> ÐA₁CB₁=ÐA₁С₁B₁ ═> AC=A₁C₁, BC=B₁C₁, ÐС = ÐС₁ ═>

ΔABC=ΔА₁В₁С₁ по первому признаку равенства треугольников.

2.Ромб. Определение, свойства, признаки.

Ромб является разновидностью четырехугольника.

Определение:Ромбом называется параллелограмм, у которого все стороны равны.

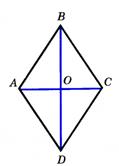
На рисунке изображён параллелограмм ABCD у которого AB=BC=CD=DA. По определению этот параллелограмм – ромб. АС и ВD – диагонали ромба. Поскольку ромб – параллелограмм, для него справедливы все свойства и признаки параллелограмма.

Свойства:

1) В ромбе противоположные углы равны (ÐA=ÐC, ÐB=ÐD)

2) Диагонали ромба точкой пересечения делятся пополам. (BО=ОD, AО=ОC)

3) Диагонали ромба взаимно перпендикулярны и делятся его углы пополам. (АС 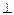DВ, ‌‌ÐАBО=ÐОВС, ÐADО=ÐОDC, ‌‌ÐBСО=ÐDСО, ÐDАО=ÐВАО ) (особое свойство)

4)Сумма углов, прилежащих к одной стороне равна 180⁰ (ÐA+ÐВ= ÐС+ÐD=ÐВ+ÐC=ÐА+ÐD=180⁰)

Обратные утверждения являются признаками ромба:

1) Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм – ромб

2) Если диагональ параллелограмма делит его углы пополам, то этот параллелограмм ромб.

3)если в параллелограмме все стороны равны, то он является ромбом.

Запись на доске.

Свойства:

1) ÐA=ÐC, ÐB=ÐD2) BО=ОD, AО=ОC

3) АС 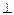DВ, ‌‌ÐАBО=ÐОВС, ÐADО=ÐОDC, ‌‌ÐBСО=ÐDСО, ÐDАО=ÐВАО

4)ÐA+ÐВ= ÐС+ÐD=ÐВ+ÐC=ÐА+ÐD=180⁰

Обратные утверждения являются признаками ромба:

1) Если ABСD – парал-м, и АС 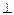DВ, то – ABСD - ромб.

2) Если ABСD – парал-м, и АС и DВ - биссектрисы, то – ABСD - ромб.

3)Если ABСD – парал-м, и АС=DВ и BC=AD, то – ABСD - ромб.

Задача.

Билет № 4