Сфера, описанная около многогранника
Комбинации многогранников и круглых тел
Понятия сферы и шара.
Сферой называется фигура, состоящая из множества всех точек пространства, расстояние от каждой из которых до данной точки О равно данному положительному числу r. Точка О называется центром сферы, а отрезок, соединяющий точку с любой точкой сферы, – ее радиусом. Все радиусы сферы имеют длину r. Число r называется радиусом сферы.
Сфера разбивает множество всех точек пространства, не принадлежащих ей, на два подмножества: внутреннюю и внешнюю области относительно сферы. Внутренней области принадлежат те точки пространства, расстояние от каждой из которых до центра меньше радиуса, а внешней области – те точки, расстояние от каждой из которых до центра больше радиуса.
Шаром называется фигура, состоящая из множества всех точек пространства, расстояние от каждой из которых до данной точки О не больше данного положительного числа r. Точка О называется центром шара, а число r – его радиусом. Сфера с центром О радиуса r называется поверхностью или границей шара. Все точки шара, не принадлежащие его поверхности, называются внутренними точками шара или точками, лежащими внутри шара. Таким образом, шар есть фигура, состоящая из объединения всех точек сферы (поверхности шара) и множества всех внутренних точек относительно этой сферы.
Касательная плоскость к поверхности шара называется касательной плоскостью к шару. Плоскость является касательной к шару тогда и только тогда, когда она проходит через точку поверхности шара перпендикулярно к радиусу, проведенному в эту точку. Отметим также, что через каждую точку поверхности шара проходит одна и только одна плоскость, касательная к шару.
Сфера, описанная около многогранника.
Определение. Сфера называется описанной около многогранника, если все вершины многогранника лежат на сфере.
Теорема 1.Около любой треугольной пирамиды можно описать сферу.
Множество точек, равноудаленных от вершин основания пирамиды есть перпендикуляр, проведенный из центра описанной окружности около основания (ГМТ в пространстве равноудаленных от вершин данного многоугольника существует, если около этого многоугольника можно описать окружность, и есть перпендикуляр, проведенный к плоскости этого многоугольника через центр описанной окружности). Центром описанной окружности является точка пересечения серединных перпендикуляров основания пирамиды.
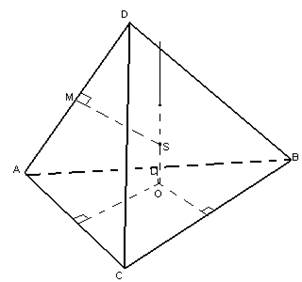
Чтобы найти центр описанной сферы, проведем плоскость через точку М – середину бокового ребра AD. Эта плоскость пересечет перпендикуляр (указанный ранее) в точке S. По построению SA=SB=SC, а также из того, что треугольник ASD равнобедренный (также по построению) следует, что SA=SD. Следовательно, расстояния от всех вершин пирамиды до точки S равны, и это расстояние равно радиусу описанной сферы около пирамиды ABCD (SA=SB=SC=SD=R).
Пример 1. Найти радиус сферы, описанной около правильного тетраэдра. 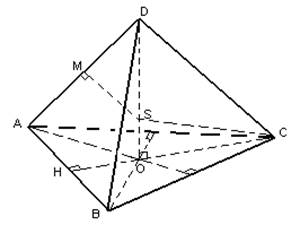
Рассмотрим треугольник SOC. Он будет прямоугольным с прямым углом O ( по построению OD будет являться высотой пирамиды).
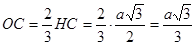 , так как О – точка пересечения медиан.
, так как О – точка пересечения медиан.
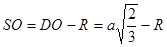 , где DO – высота пирамиды.
, где DO – высота пирамиды.
Тогда по теореме Пифагора следует, что 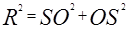 или
или
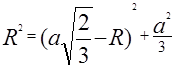
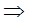
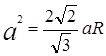
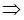
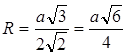
Ответ: Радиус сферы, описанной около правильного тетраэдра равен 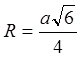
Теорема 2. Если около основания пирамиды можно описать окружность, то около пирамиды можно описать сферу.
Мы уже рассмотрели частный случай. В общем случае доказывается аналогично.
Теорема 3 . Около наклонной призмы описать сферу нельзя; около прямой призмы можно описать сферу, если около основания призмы можно описать окружность.
1) Рассмотрим вначале случай, когда призма наклонная (в качестве примера возьмем треугольную призму). Точка, равноудаленная от точек А, В и С будет находиться на прямой OS1, которая перпендикулярна плоскости треугольника АВС и основание перпендикуляра находится в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника АВС.
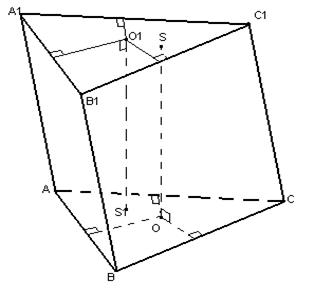
Аналогично, точки, равноудаленные от точек А1, В1, С1 лежат на перпендикуляре к плоскости треугольника А1В1С1 – О1S. Так как призма наклонная, то прямые OS1и О1S будут параллельными, но не совпадающими. А это значит, что они не будут иметь общих точек, следовательно: не найдется такой точки, расстояние от которой до всех вершин призмы являлось бы одинаковым, что аналогично невозможности построения сферы, описанной около наклонной призмы.
2) Рассмотрим прямую призму, возле основания которой можно описать окружность. Точки О и О1 – центры описанных окружностей возле нижнего и верхнего основания соответственно. Так как призма прямая, то прямая ОО1 будет являться перпендикуляром к плоскостям основания.
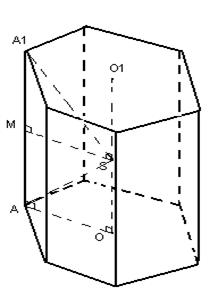
Тогда плоскость, проходящая через середины боковых ребер будет параллельна плоскости основания и будет пересекать ОО1 в точке S – середине ОО1. Тогда расстояние от всех вершин призмы до тачки S будет одинаковым (по построению), следовательно, S – центр сферы, описанной около правильной призмы.
Итак, мы убедились, что возле наклонной призмы описать сферу нельзя, а возле прямой призмы – возможно, если возле ее основания можно описать окружность.
Теорема 4. Около усеченной пирамиды можно описать сферу тогда и только тогда, когда около ее оснований можно описать окружности и прямая, соединяющая центры этих окружностей, перпендикулярна к плоскостям оснований.
Первое условие означает, что перпендикуляры, которые являются ГМТ, равноудаленных от вершин многоугольников оснований будут существовать, а второе, – что они совпадают, следовательно, найдется такая точка, которая будет равноудалена от всех вершин усеченной пирамиды.
