Основные свойства корней
Корень n-й степени, его свойства.
Арифметическим корнем n-й степени из числа а называют неотрицательное число , n-я степень которого равна а.
Обозначается арифметический корень n-й степени из числа а
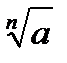 ,
,
где n- показатель корня,
а- подкоренное выражение.
Знак 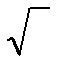 называют еще радикалом.
называют еще радикалом.
Арифметический корень второй степени называется корнем квадратным и обозначается √, арифметический корень третьей степени называется кубическим корнем о обозначается 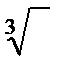
Например :
а) 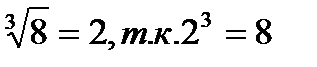 и 2≥0;
и 2≥0;
б) 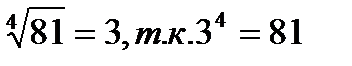 и 3≥0;
и 3≥0;
в) 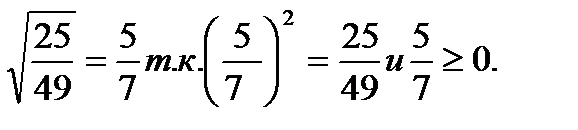
Из определения арифметического корня n-й степени следует, что при четом n подкоренное выражение должно быть больше или равно нулю, а значит и значение такого корня тоже неотрицательно, например: арифметический корень 4-й степени из числа -81 не существует, так как ни одно число в четвертой степени не даст -81 ( при возведении в четную степень значение выражения всегда неотрицательно).
При нечетном показателе корня подкоренное выражение может быть отрицательным, и тогда минус может быть вынесен за знак коня.
Например: 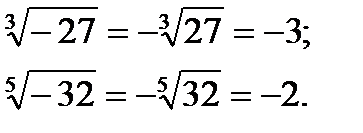
Уравнение хn=а.
Уравнение хn=а при нечетном n имеет единственное решение х= 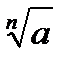 .
.
Например : х3=-125;
х= 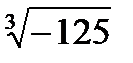 ;
;
х=- 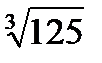 ;
;
х=-5.
Для наглядности сделаем проверку:
(-5)3=-125;
-125=-125- верно.
Ответ : х=-5.
Уравнение хn=а при четном n имеет и положительном а имеет два корня
х=± 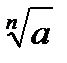 .
.
Например:
х4=16;
х1= 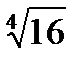 ; х2=-
; х2=- 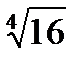 ;
;
х1=2; х2=-2.
Можно убедиться при проверке, что 24=16 и (-2)4=16.
Ответ : ±2.
Иногда нужно применить такое свойство арифметического корня n-й степени:
|х|, если n четно;
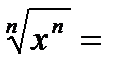 х, если n нечетно.
х, если n нечетно.
х, если х≥0;
 Вспомним, что |х|= -х, если х<0.
Вспомним, что |х|= -х, если х<0.
Например :
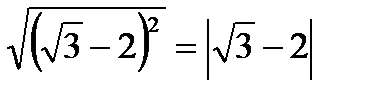 .
.
Так как 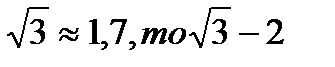 <0, следовательно
<0, следовательно
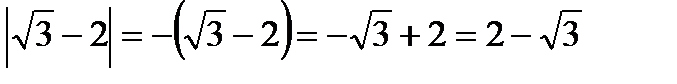 .
.
Основные свойства корней.
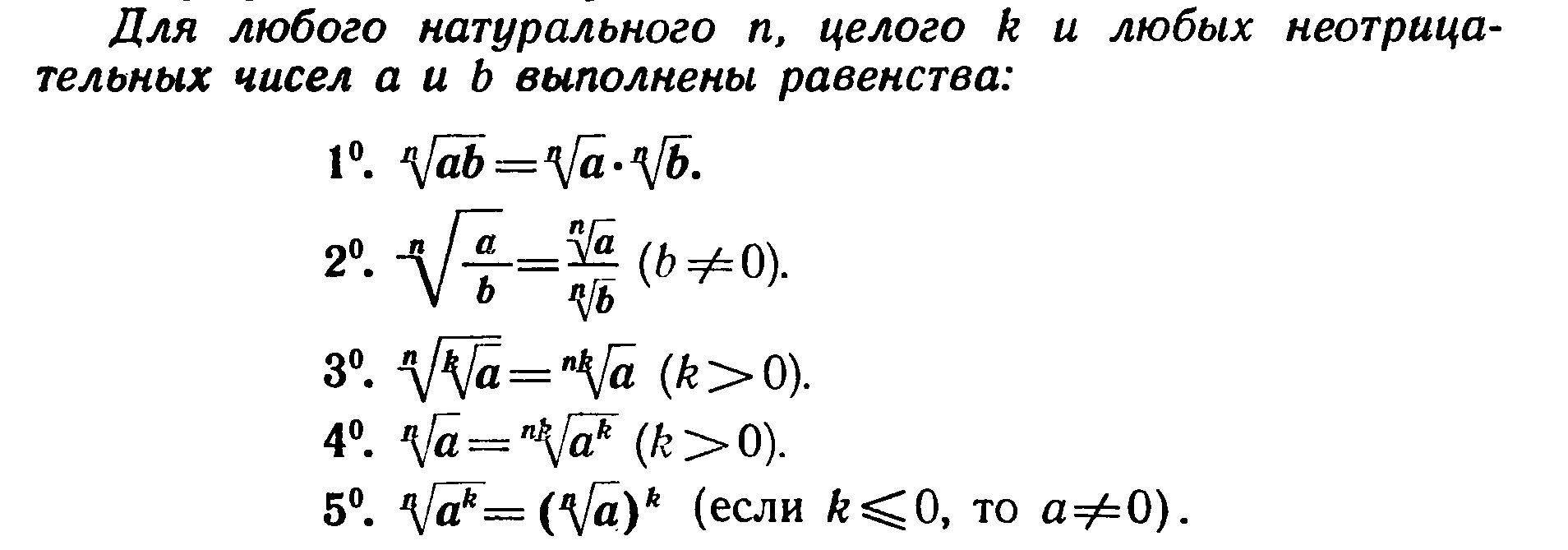
Для арифметического корня n-й степени, как и для квадратного корня, существуют операции внесения множителя под знак корня и вынесение множителя из-под знака корня.
Например :
2 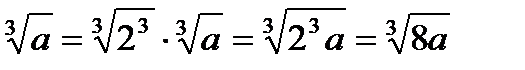 .
.
Из примера видно, что для внесения множителя под знак корня n-й степени его нужно
возвести в n-ю степень. Нужно помнить, что под знак с четным показателем мы имеем право внести только положительный множитель, например:
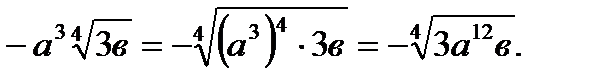
Аналогично производится вынесение множителя из-под знака корня , например:
а) 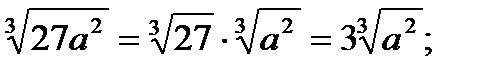
б) 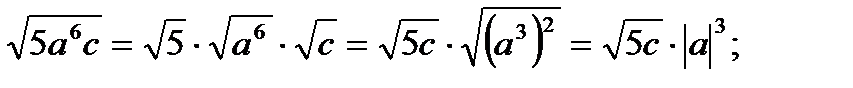
в) 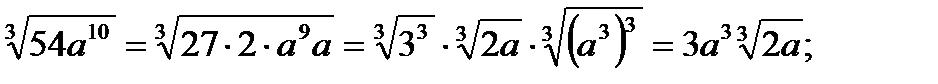
формулой n-го члена ап: an= a1+ d · (n - 1)
формулой n-го члена гп: 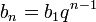
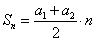 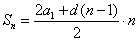 |
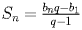 , , 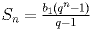 , если , если 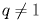 . . |
Функции y=kx (где k - любое натуральное число). Прямая пропорциональность, график прямая.
Свойства:
область определения - R
область значений - R
нечетная
при к >0 функция возрастает, при к <0 –убывает
| Корень квадратного уравнения (формула) |
Корни уравнения ax2 + bx + c = 0 (a ¹ 0) находят по формуле 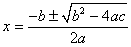 . Выражение D = b2 – 4ac называют дискриминантом квадратного уравнения. Квадратное уравнение имеет действительные корни (или корень) тогда и только тогда, когда его дискриминант неотрицателен. Если . Выражение D = b2 – 4ac называют дискриминантом квадратного уравнения. Квадратное уравнение имеет действительные корни (или корень) тогда и только тогда, когда его дискриминант неотрицателен. Если 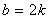 , можно применить формулу , можно применить формулу 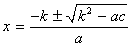 . . |
| если просто уравнений, а не систем, то алгоритм прост: 1. неизвестные влево, сложить коэфициенты; числа вправо, также сложить (с учетом знака конечно) 2. разделить правую часть на коэфициент при неизвестном 2прим. если коеф.=0 и справа 0 -- любое число есть решение уравнения если коеф.=0 а справа не 0 -- уравнение решения не имеет |
