Методы вычисления определённых интегралов

При вычислении определённых интегралов используются методы непосредственного интегрирования, замены переменной (подста-

новки) и интегрирования по частям.

Непосредственное интегрирование предполагает сведение данного интеграла с помощью алгебраических и арифметических преобразований к формулам таблицы основных интегралов и использование формулы Ньютона-Лейбница.

Примеры 10-11. Вычислить интегралы: а) 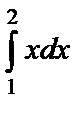; б) .

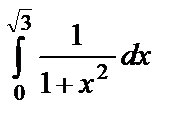Решение. а) = ;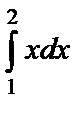

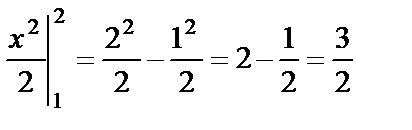б) = .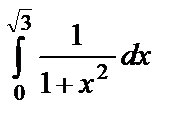

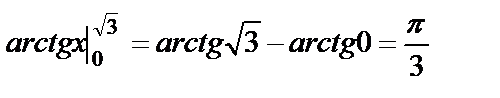Метод замены переменной в определённом интеграле предполагает следующее. Пусть выполнены условия:

функция 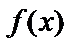непрерывна на отрезке ;

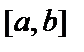функция 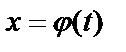определена на отрезке 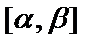и имеет на нём непрерывную производную;

, .

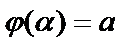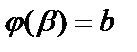Тогда определённый интеграл 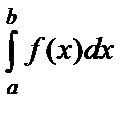может быть вычислен с помощью введения новой переменной и при этом справедлива формула 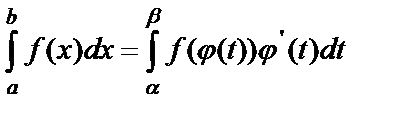. Часто вместо замены 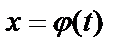применяют обратную замену .

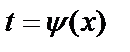Примеры 12–13. Вычислить интегралы: а) 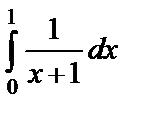; б) .

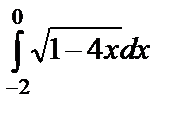Решение. а) Выполним замену 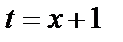, 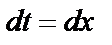. Вычислим пределы интегрирования для переменной t:

x
t

Тогда = .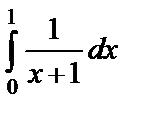

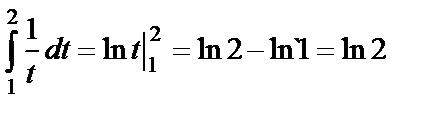б) Выполним замену 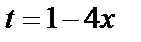и продифференцируем обе части равенства: 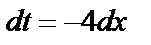, 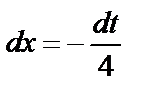. Изменим пределы интегрирования:

x	-2
t

В результате =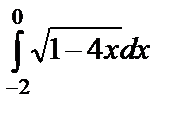

.

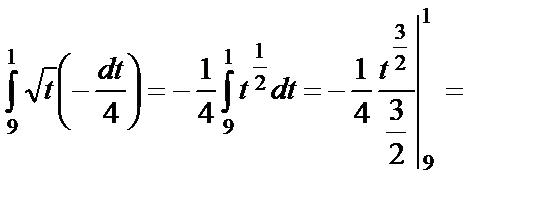
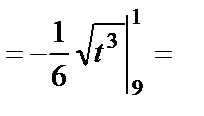
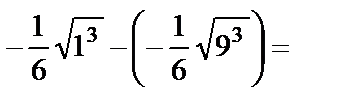
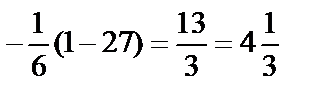Пусть функци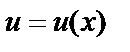и и 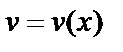имеют непрерывные производные на отрезке 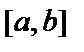. Тогда для определённого интеграла справедлива формула интегрирования по частям .

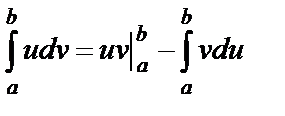Пример 14. Вычислить интеграл .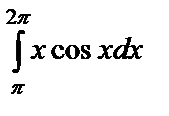

Решение. Положим u=x, тогда du=dx. Оставшуюся часть подынтегрального выражения примем за dv: 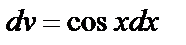. Проинтегрируем это выражение: 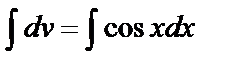, 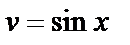. Тогда по формуле интегрирования по частям получим = =

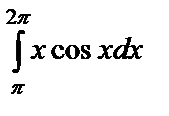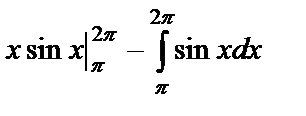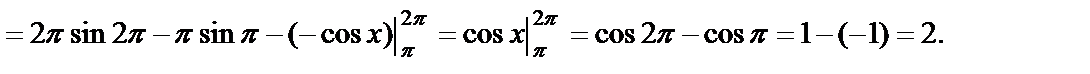
Вычисление площадей плоских фигур

Согласно геометрическому смыслу определённого интеграла площадь криволинейной трапеции, расположенной выше оси абсцисс, равна определённому интегралу от функции 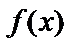: 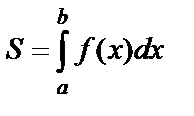. Если криволинейная трапеция расположена ниже оси абсцисс, то площадь такой трапеции вычисляется по формуле: .

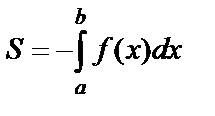y = f(x)

y = f(x)

0

0

х

х

у х

у

а

а

b

b

Пусть фигура ограничена снизу графиком функции 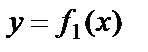, сверху – графиком функции 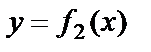, слева – прямой x=a и справа – прямой x=b.

b

а

0

y

y = f2(x)

y = f1(x)

x

Тогда площадь фигуры, ограниченной этими линиями, вычисляется по формуле: .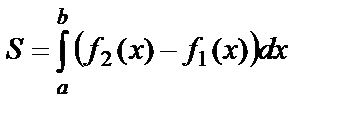

Пример 15. Вычислить площадь фигуры, ограниченной линиями , .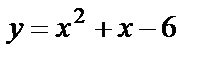

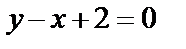Решение. Графиком функции 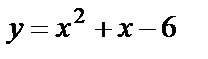является парабола, ветви которой направлены вверх. Найдём точки пересечения параболы с осью Ох: 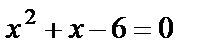, , 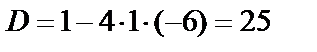, 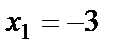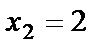. Уравнение прямой 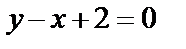запишем в виде 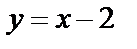. Изобразим эти линии в системе координат и заштрихуем фигуру, ограниченную этими линиями.

у

-2

-3

•

•

•

•

х

Найдём абсциссы точек пересечения линий: 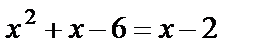, , 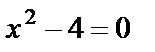, 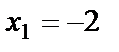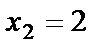. Тогда площадь заштрихованной фигуры равна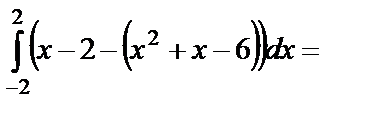

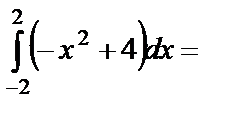
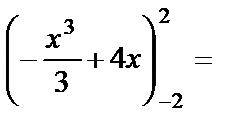
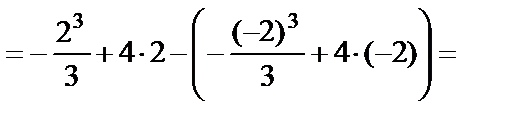
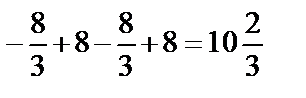(кв. ед.).

Вопросы для самоконтроля знаний

1. Что называется первообразной функцией?

2. Что называется неопределённым интегралом от данной функции?

3. Как формулируются основные свойства неопределённого интеграла?

4. Какие существуют основные методы интегрирования?

5. В чём суть непосредственного интегрирования?

6. В чём суть метода замены переменной (метода подстановки)?

7. В чём суть метода интегрирования по частям?

8. Что называется определённым интегралом от данной функции на данном отрезке?

9. Каков геометрический смысл определённого интеграла?

10. Как формулируются основные свойства определённого интеграла?

11. Как записывается формула Ньютона-Лейбница?

12. Как выполняется замена переменной в определённом интеграле?

13. Как записывается формула интегрирования по частям в определённом интеграле?

14. Как вычисляется площадь плоской фигуры в прямоугольной системе координат?