Линейный коэффициент корреляции
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ В
ЭКОНОМИЧЕСКИХ РАСЧЕТАХ
Основные понятия в корреляционном и регрессионном анализе
В математике существуют два понятия, отражающие причинно-следственные связи между признаками: функциональная и корреляционная зависимость.
Под функциональной зависимостью понимается такая связь между величинами, когда значение зависимой величины – функции – полностью определяется значениями зависимых переменных.
Корреляционная зависимость имеет место, когда каждому значекнию одной (результативной) величины соответствует множество случайных значений другой, возникающей с определенной вероятностью.
При изучении экономических явлений мы имеем дело не с функциональной, а с корреляционной зависимостью. С помощью корреляционного и регрессионного анализа можно рассчитать коэффициенты корреляции, которые оценивают силу связи между отдельными показателями, подобрать
уравнение регрессии, которое определяет форму этой связи, и установить достоверность существования этой связи.
Процесс корреляционного и регрессионного анализа экономических процессов состоит из следующих этапов:
- предварительная обработка статистических данных и выбор основных факторных признаков, влияющих на результативный показатель;
- оценка тесноты связи и выявление формы существующей связи между результативным и факторными признаками;
- разработка модели (многофакторной) изучаемого явления и ее анализ;
- применение полученных результатов проведенного анализа для принятия управленческих решений.
Перед корреляцией стоят две основные задачи. Первая заключается в выявлении, как изменяется в среднем результативный признак в связи с изменением факторного. Эта задача решается нахождением уравненимя связи.Вторая задача определяет степень влияния искажающих факторов. Эту задачу решают путем изучения показателей тесноты связи. Такими показателями являются коэффициенты корреляции и корреляционное отношение.
2. Результативный и факторный признаки. При изучении влияния одних признаков явлений на другие из цепи признаков, характеризующих данное явление, выделяются два - признака—факторный (влияющий на результат) и результативный. Необходимо установить, какой из признаков является факторным и какой результативным. В этом помогает прежде всего логический анализ.
Пример. Себестоимость промышленной продукции отдельного предприятия зависит от многих факторов, в том числе от объема продукции на данном предприятии. Себестоимость продукции выступает в этом случае как результативный признак, а объем продукции — как факториальный.
Другой пример. Чтобы судить о преимуществах крупных предприятий перед мелкими, можно рассмотреть, как увеличивается производительность труда рабочих крупных предприятий, и выявить зависимость производительности труда от увеличения размеров предприятия.
3. Понятие об уравнение связи. Уравнение этой функции будет уравнением связи между результативным и факториальным признаками.
Уравнение связи находится с помощью способа наименьших квадратов, который требует, чтобы сумма квадратов отклонений эмпирических значений от значений, получаемых на основании уравнения связи, была минимальной.
Применение способа наименьших квадратов позволяет находить параметры уравнения связи при помощи решения системы так называемых нормальных уравнений, различных для связи каждого вида.
Чтобы отметить, что зависимость между двумя признаками выражается и среднем, значения результативного признака, найденные по уравнению связи, обозначаются Ух.
Зная уравнение связи, можно вычислить заранее среднее значение результативного признака, когда значение. факториального признака известно. Таким образом, уравнение связи является методом обобщения наблюдаемых статистических связей, методом их изучения.
Применение той или иной функции в качестве уравнения связи разграничивает связи по их форме: линейную связь и криволинейную связь (параболическую, гиперболическую и др.).
Рассмотрим уравнения связи для зависимостей от одного признака при разных формах связи, (линейной, криволинейной параболической, гиперболической) и для множественной связи.
4. Линейная зависимость между признаками. Уравнение связи как уравнение прямой Ух==ао+а1х применяется в случае равномерного нарастания результативного признака с увеличением признака факториального. Такая зависимость будет зависимостью линейной (прямолинейной).
Параметры уравнения прямой линии ао и а1 находятся путем решения системы нормальных уравнений, получаемых по способу наименьших квадратов:
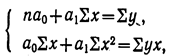
Примером расчета параметров уравнения и средних значений результативного признака Ух может служить следующая таблица, являющаяся результатом группировки по факториальному признаку и подсчета средних по результативному признаку.
Группировка предприятий по стоимости основных средств и подсчет сумм необходимы для уравнения связи.
| Группы предприятий по стоимости основных средств | Выработка продукции на одного работника(тыс.руб) | Среднее значение интервала | Х 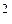  | У * Х | Ух |
| До 1 млн. руб, 1 – 2 2 – 3 3 – 4 4 – 5 5 и более | 6,5 7,0 8,0 8,5 | 0,5 1,5 2,5 3,5 4,5 5,5 | 0,25 2,25 6,25 12,25 20,25 30,25 | 2,0 9,0 13,75 24,50 36,0 46,75 | 4,35 5,21 6,07 6,93 7,79 8,65 |
| Итого | 40,0 | 18,0 | 71,50 | 132,0 | 40,0 |
Из таблицы находим: n==6; 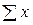 =18;
=18; 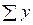 =39,0;
=39,0; 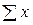
 =71,5
=71,5
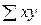 = 132.0. Строим систему двух уравнений с двумя неизвестными:
= 132.0. Строим систему двух уравнений с двумя неизвестными:
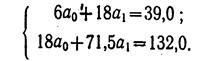
Поделив каждый член в обоих уравнениях на коэффициенты при aо получим:
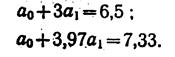
 Вычтем из второго уравнения первое: 0,97а1=0,83; а1==0,86. Подставив значения а1 в первое уравнение aо+3*0,86 =6,5, найдем ао=6,5—2,58=+3,92.
Вычтем из второго уравнения первое: 0,97а1=0,83; а1==0,86. Подставив значения а1 в первое уравнение aо+3*0,86 =6,5, найдем ао=6,5—2,58=+3,92.
Уравнение связи примет вид: yx=3,92+0,86х. Подставив в это уравнение соответствующие х, получим значения результативного признака, отражающие среднюю зависимость у от х в виде корреляционной зависимости.
Заметим, что суммы, исчисленные по уравнению и фактические, равны между собой. Изображение фактических и вычисленных значений на рис. 4 показывает, что уравнение связи отображает наблюденную зависимость в среднем.
5. Параболическая зависимость между признаками. Параболическая зависимость, выражаемая уравнением параболы 2-го порядка уx =ао+a1x+a2x2, имеет место при ускоренном возрастании или убывании результативного признака в сочетании с равномерным возрастанием факториального признака.
Параметры уравнения параболы aо; а1; а2, вычисляются путем решения системы 3 нормальных уравнений:
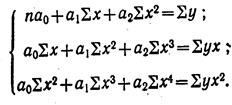
Возьмем для примера зависимость месячного выпуска продукции (у) от величины стоимости основных средств (х). Оба показателя округлены до миллионов рублей. Расчеты необходимых сумм приведем в табл. 5.
По данным таблицы составляем систему уравнений:

6. Уравнение гиперболы. Обратная связь указывает на убывание результативного признака при возрастании факториального. Такова линейная связь при отрицательном значении а1. В ряде других случаев обратная связь может быть выражена уравнением гиперболы
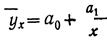
Параметры уравнения гиперболы ао и а1 находятся из системы нормальных уравнений:
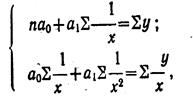

7. Корреляционная таблица. При большом объеме наблюдений, когда число взаимосвязанных пар велико, парные данные легко могут быть расположёны в корреляционной таблице, являющейся наиболее удобной формой представления значительного количества пар чисел.
В корреляционной таблице один признак располагается в строках, а другой — в колонках таблицы. Число, расположенное в клетке на пересечении графы и колонки, показывает, как часто встречается данное значение результативного признака в сочетании с данным значением факториального признака.
Для простоты расчета возьмем небольшое число наблюдений на 20 предприятиях за средней месячной выработкой продукции на одного рабочего (тыс. руб.—у) и за стоимостью основных производственных средств (млн. руб.—.х).
В обычной парной таблице эти сведения располагаются так:
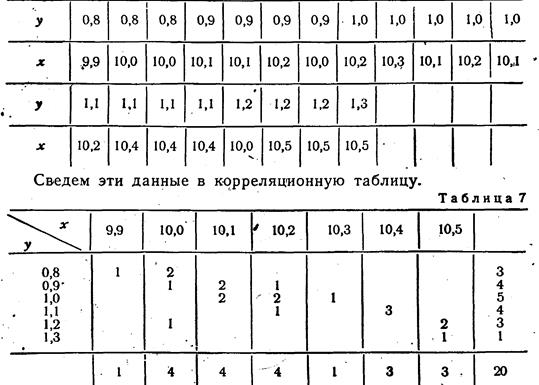
Итоги строк у показывают частоту признака nу, итоги граф х — частоту признака nx. Числа, стоящие в клетках корреляционной таблицы, являются частотами, относящимися к обоим признакам и обозначаются, nxy.
Корреляционная таблица даже при поверхностном знакомстве дает общее представление о прямой и обратной связи. Если частоты расположены по диагонали вниз направо, то связь между признаками прямая (при увеличивающихся значениях признака в строках и графах). Если же частоты расположены по диагонали вверх направо, то связь обратная.
8. Корреляционное отношение. Если произведено измерение явления по двум признакам, то имеется возможность находить меры рассеяния (главным образом дисперсию) по результативному признаку для одних и тех же значений факториального признака.
Дана, например, корреляционная таблица двух взаимозависимых рядов, в которых для простоты имеется лишь три .значения факториального признака количества внесенных удобрений (х), а результативный признак—урожайность (у)—значительно колеблется. Таблица 16
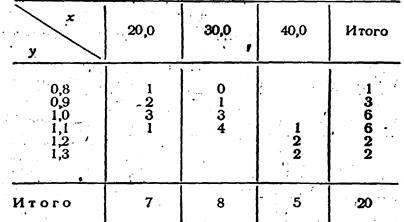
Каждая группа участков с разной урожайностью имела разное количество внесенных удобрений. Так, когда вносилось удобрений по 20 г/ урожайность' на разных участках была равной: на одном участке она составила 0,8 т, на двух участках— 0,9 т, на трех— 1,0 т и на одном — 1,1 т. Найдем среднюю урожайность и дисперсию по урожайности для этой группы участков.

Для группы участков с количеством внесенных удобрений 30,0 г средняя урожайность составит:

Вычислим аналогичные характеристики для группы участков. получивших удобрений по 40 т:
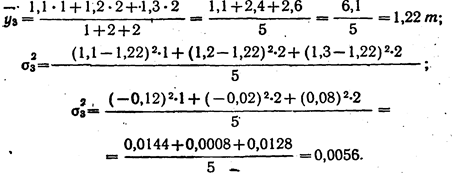
Из этих данных можно определить также средний урожай всех 20 участков, независимо от количества внесенных удобрений, т. е. общую среднюю:
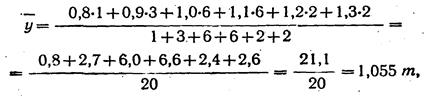
и меру колеблемости (дисперсию) средней урожайности групп •около общей средней. Эту дисперсию называют межгрупповой ^дисперсией и обозначают б2
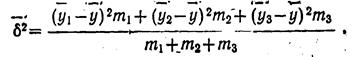
где уi—средние урожайности по группам участков, отличающихся количеством внесенных удобрений; m1,m2,m3,—численности групп. Межгрупповая дисперсия для данного примера составит:

Межгрупповая дисперсия показывает рассеяние, возникающее за счет факториального признака. В данном примере У= == 0,01&247 является показателем рассеяния урожайности, возникшего за счет разности в количестве внесенных удобрений.
Однако, кроме межгрупповой дисперсии, можно вычислить и дисперсию как показатель рассеяния за счет остальных факторов (если называть так все прочие факторы, кроме удобрений). Этот показатель явится средней (взвешенной) величиной из показателей рассеяния (дисперсий) по группам участков

Это практически означает, что можно получить общую меру рассеяния (дисперсию) для всех 20 участков, если имеются сведения о средних и дисперсиях по группам участков, отличающихся количеством внесенных удобрений. Следовательно, общая дисперсия по урожайности для 20 участков составит;
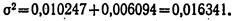
Формулы для исчисления межгрупповой и средней из групповых дисперсий можно сокращенно записать так:
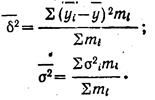
Расчет общей дисперсии, внутригрупповой и межгрупповой дисперсии позволяет делать некоторые выводы о мере влияния факториального признака на колеблемость признака результативного. Эта мера влияния находится при помощи корреляционного отношения:
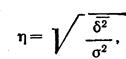

Значит, колеблемость по урожайности участков на 78% зависит от колеблемости количества внесенных удобрений.
Линейный коэффициент корреляции
При изучении тесноты связи между двумя взаимозависимыми рядами применяется линейный коэффициент корреляции, который показывает, существует ли и насколько велика связь между этими рядами. Он может принимать значения в пределах от –1 до +1.
Если линейный коэффициент корреляции отрицателен, то это говорит об обратной связи между признаками; если же он положителен – о прямой связи. Если он равен нулю, то связи между признаками нет, а если равен 1-це, то между признаками существует не корреляционная, а функциональная связь.
Для расчета линейного коэффициента корреляции пользуются следующей формулой::
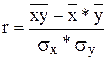
где 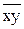 – среднее значение произведения х на у;
– среднее значение произведения х на у;
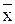 и
и 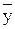 – среднее значение соответствующих признаков;
– среднее значение соответствующих признаков;
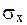 и
и 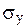 – средние квадратические отклонения, найденные по признаку х и по признаку у.
– средние квадратические отклонения, найденные по признаку х и по признаку у.
10.Совокупный коэффициент корреляции:
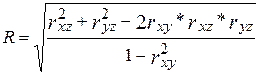 ,
,
где r – линейные коэффициенты корреляции, а подстрочные знаки показывают, между какими признаками они исчисляются.
