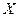Операции над множествами

Федеральное агентство по образованию

Тверской колледж имени А.Н. Коняева

«Множества»

Учебно-методическое пособие по предмету «Математика»

для студентов первого курса

Тверь,

Одобрено предметной (цикловой) Заместитель директора

комиссией по учебной работе

Председатель Дац В.А. Виноградов Н.Е.

____________________ _____________________

Составил: Бодров Е.Н.

__________________

Учебное пособие содержит теоретический и практический материал по теме «Множества». Пособие предназначено для студентов, изучающих дисциплины «Математика», «Дискретная математика», а также может быть полезно преподавателям математики.

Оглавление

ВВЕДЕНИЕ..................................................................................................... 4

1. Основные понятия теории множеств.......................................................... 5

2. Изображение множеств............................................................................... 6

3. Операции над множествами........................................................................ 7

4. Основные свойства операций над множествами........................................ 9

5. Примеры решения задач.......................................................................... 10

6. Задачи для самостоятельного решения.................................................... 12

Приложение А............................................................................................... 15

Список литературы....................................................................................... 22

ВВЕДЕНИЕ

Теоретико-множественные понятия встречаются практически во всех разделах современной математики и составляют ее фундамент. Теоретико-множественный подход способствует развитию общей культуры студентов, помогает видеть связи между явлениями. Таким образом, теоретико-множественный подход при изучении курса математики создает благоприятные условия для целенаправленного изучения языка математики, способствует повышению научности и четкости в изложении материала, содействует выявлению связей между различными разделами математики, помогает развитию математической культуры студентов.

Основным средством формирования теоретико-множественных понятий и их применения при изучении программного материала является специальный подбор системы упражнений и задач. Предлагаемое пособие по теме «Множества» содержит как теоретический, так и практический материал. Рассматриваемая система упражнений рассчитана на овладение студентами общими методами рассуждений, активизацию их мыслительной деятельности, выработку творческого подхода к решению задач, установление связи теоретико-множественных понятий с окружающей действительностью.

Основные понятия теории множеств

Понятия множество, элементы множества – одни из основных неопределяемых понятий современной математики.

Под множеством (семейством, набором, ансамблем) понимается совокупность объектов, объединенных некоторым признаком, свойством. Объекты, из которых состоит множество, называются элементами.

Пример 1.1. 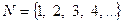- множество натуральных чисел, 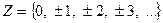- множество целых чисел,

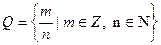- множество рациональных чисел, 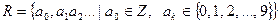- множество действительных чисел.

Запись 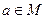означает, что элемент 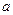принадлежит множеству .

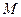Запись 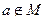означает, что элемент 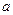не принадлежит множеству .

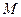Для обозначения множеств будем применять прописные буквы латинского алфавита, а элементов – строчные буквы латинского алфавита.

Способы задания множества:

1. Перечислением, то есть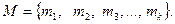

2. Указанием свойства, которым обладают элементы, принадлежащие этому множеству. Данное свойство называется характеристическим. Множество записывается следующим образом:

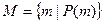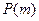, - характеристическое свойство.

Пример 1.2. 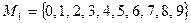- множество цифр, .

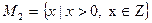Определение 1.1. Множество называется пустым, если оно не содержит ни одного элемента. Обозначение - Ø.

Определение 1.2. Множество 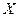называется подмножеством множества 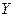, если всякий элемент множества 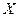является элементом множества 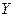. Обозначение - .

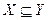Определение 1.3. Универсальным называют множество 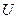, состоящее из всех возможных элементов, обладающих данным признаком.

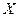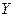Определение 1.4. Множества и называются равными, если они состоят из одних и тех же элементов.

Определение 1.5. Мощность множества 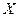- это число элементов множества 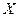. Обозначение - .

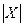Изображение множеств

Множества принято изображать с помощью кругов Эйлера-Венна. Элементы множества изображаются точками внутри круга, если они принадлежат множеству, и точками вне круга, если они не принадлежат множеству. Тот факт, что 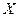является подмножеством , с помощью кругов Эйлера-Венна изображается следующим образом (рисунок 2.1).

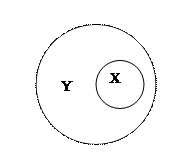
Рисунок 2.1. Иллюстрация кругами Эйлера-Венна

Операции над множествами

1. Под объединением двух множеств 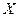и 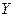(обозначение 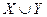) понимается множество тех и только тех элементов, которые принадлежат хотя бы одному из множеств 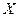и 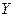(рисунок 3.1).

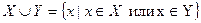
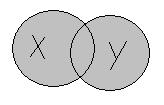
Рисунок 3.1. Объединение множеств

Пример 3.1.Даны множества 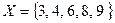и 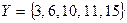. Тогда объединение этих множеств: .

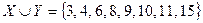2. Под пересечением двух множеств 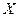и 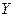(обозначение 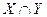) понимается множество тех и только тех элементов, которые принадлежат одновременно множествам 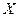и 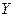(рисунок 3.2.).

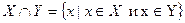
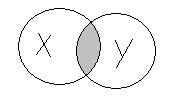
Рисунок 3.2. Пересечение множеств

Пример 3.2.Даны множества 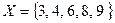и 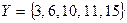. Тогда пересечение этих множеств: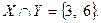

3. Разностью множеств 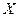и 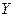(обозначение 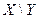) называется множество тех и только тех элементов 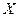, которые не принадлежат множеству 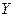(рисунок 3.3.).

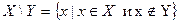
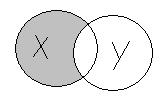
Рисунок 3.3. Разность множеств

Пример 3.3.Даны множества 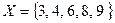и 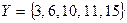. Тогда разность этих множеств: .

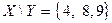4. Симметрической разностью множеств 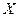и 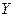(обозначения 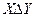или 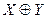) называется множество тех и только тех элементов, которые принадлежат одному из множеств, но не являются общими элементами (рисунок 3.4.).

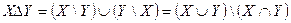
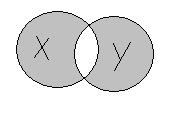
Рисунок 3.4. Симметрическая разность множеств

Пример 3.4.Даны множества 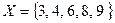и 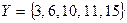. Тогда симметрическая разность этих множеств: .

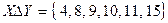5. Дополнением к множеству 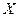(обозначение 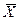) называется множество тех и только тех элементов, которые не принадлежат множеству 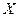, то есть дополняют его до универсального множества (рисунок 3.5.).

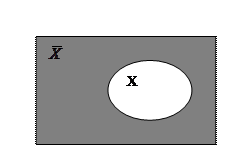
Рисунок 3.5. Дополнение к множеству