Уравнения с параметром, содержащие модуль

Решить в зависимости от значений параметра а.

| x – 3 | = a

По свойству модуля при всех 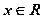левая часть уравнения неотрицательна, следовательно, при a < 0 уравнение не имеет решений.

При a = 0 x = 3.

При a > 0 x – 3 = ± a, откуда x = 3 ± a.

Ответ: при a = 0 x = 3.

при a > 0 x = 3 + a. x = 3 – a.

при a < 0 уравнение не имеет решений.

При каких значениях параметра a уравнение x = a · | x – 5 | имеет единственное решение, два решения, не имеет решения. Найдите их.

Для решения уравнения найдём нули модули x – 5 = 0 x = 5.

Раскроем модуль на двух промежутках: x ≥ 5 и x < 5.

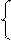1) x ≥ 5, 2) x < 5,

x = a ( x – 5 ) x = a ( – x + 5 )

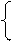
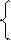x ≥ 5, x < 5,

x – ax = – 5a;x + ax = 5a;

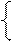x ≥ 5, x < 5,

x ( 1– a )= – 5a;x ( 1+ a )= 5a ;

Исследуем линейное уравнение Исследуем линейное уравнение

в зависимости от параметра a. в зависимости от параметра a.

x ( 1– a )= – 5a ; x ( 1+ a )= 5a;

Если 1– a = 0, т.е. a = 1, то Если 1+ a = 0, т.е. a = – 1, то

x · 0 = – 5 Уравнение не имеет x · 0 = – 5 Уравнение не имеет

решения. решений.

Если 1– a ≠ 0, т.е. a ≠ 1, то Если 1+ a ≠ 0, т.е. a ≠ – 1, то

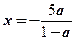- уравнение имеет 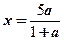- уравнение имеет

единственное решение. единственное решение.

x ≥ 5, x < 5,

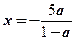, a ≠ 1; 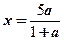, a ≠ –1;

Учтем, что x ≥ 5, т.е. Учтем, что x < 5, т.е.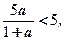

решим методом интервалов решим методом интервалов

неравенство. неравенство.

Получим a > 1. Т.е. при a > 1 Получим a > – 1. Т.е. при a > –1

уравнение будет иметь уравнение будет иметь

единственное решение 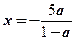единственное решение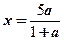

на промежутке x ≥ 5. на промежутке x < 5.

Ответим на поставленные вопросы. Наши решения покажем на координатных прямых.

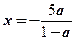
одно решение

a

нет одно два

a

решения решение решения

-1

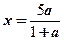
При a > 1 уравнение имеет два корня ; ;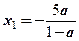

При a < – 1 уравнение не имеет решения.

При – 1< a ≤ 1 уравнение имеет одно решение, т.е. .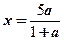

Ответ: a > 1, ; .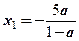

a < – 1, решений нет.

– 1< a ≤ 1, .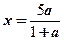

Решить самостоятельно:

При каком a уравнение имеет решения. Найдите их.

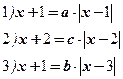
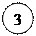При каких значениях a уравнение | x + 3| · ( x – 3 ) + a = 0 имеет ровно 3 решения?

Найдем нули модуля: x + 3 =0; x = – 3.

Раскроем модуль на двух промежутках:

x ≥ – 3 x < – 3

x ≥ – 3, x < – 3

( x + 3) ( x – 3 ) + a = 0; (– x – 3) ( x – 3 ) + a = 0;

Исследуем уравнение Исследуем уравнение

( x + 3) ( x – 3 ) + a = 0; (– x – 3) ( x – 3 ) + a = 0;

x² – 9 + a = 0; – ( x² – 9 ) = – a ;

x² = 9 – a ; x² – 9 = a ;

при 9 – a ≥ 0, т.е. a ≤ 9 x² = a + 9;

уравнение имеет два корня при a + 9 ≥ 0, т.е. a ≥ – 9

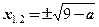. уравнение имеет два корня

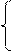x ≥ – 3; a ≥ – 9

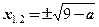; a ≤ 9 x < – 3;

Учтем, что x ≥ – 3 Учтем, что x < – 3

при 9 – a ≥ 0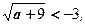

неравенство имеет решение, решения нет.

т.е. a ≤ 9.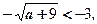

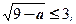
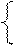
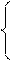
a + 9 ≥ 0,

a + 9 > 9,

неравенство имеет решение Т.е. при a > 0

a ≤ 9; уравнение имеет один корень

a ≥ 0; т.е. 0 ≤ a ≤ 9;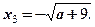

Т.е. при 0 ≤ a ≤ 9 уравнение

имеет два различных корня.

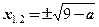, при a = 3

уравнение имеет два равных

корня .

Ответим на поставленный вопрос.

При 0 ≤ a < 9 уравнение имеет 3 корня.

a

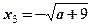
нет три одно

a

решения решения решение

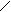
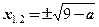
два два

решения решения

Ответ: при 0 ≤ a < 9 три корня.

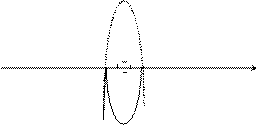
При каких значениях a уравнение | x + 3| · ( x – 3 ) + a = 0 имеет ровно 3 решения? (Графический способ).

| x + 3| · ( x – 3 ) = – a

Построим графики, заданные в левой и правой частях:

1) y = | x + 3| · ( x – 3 )

Найдем нули модуля: x + 3 =0; x = – 3.

Раскроем модуль на двух промежутках: x < – 3; x ≥ – 3.

x ≥ – 3; x < – 3;

y = ( x + 3) ( x – 3 ) = x² – 9; y = – ( x + 3) ( x – 3 ) = 9 – x²;

2) y = – a – линейная функция, график прямая, параллельная оси OY.

x

Эскиз графиков. y

-3

y = – a

-9

Ответ: 0 < a < 9.

При каких значениях a уравнение имеет единственное решение?

ОДЗ: x²+ 8x + 12 ≠ 0; x ≠ – 6; x ≠ –2;

Найдем нули модуля: 2x + 6 = 0; x = –3;

Раскроем модуль на двух промежутках: x ≥ –3 и x < –3.

1) x ≥ –3; и 2) x < –3.

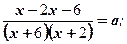
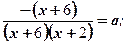
x ≥ –3; x < –3.

x ≥ –3; x < –3.

Исследуем уравнение: Исследуем уравнение

x ≠ – 6; x ≠ –2;

Если a = 0; 0 ∙ x = 3 Если a = 0; 0 ∙ x = – 1

решения нет. решения нет.

a ≠ 0; a ≠ 0;

единственное решение. единственное решение.

x ≥ –3; x < –3;

a ≠ 0; a ≠ 0;

Учтем, что x ≥ –3; т.е. Учтем, что x < –3; т.е.

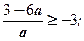
Решим методом интервалов Решим методом интервалов

неравенство. неравенство

Получим 0 < a ≤ 1. Получим 0 < a < 1.

Т.е. при 0 < a ≤ 1 уравнение Т.е. при 0 < a < 1 уравнение

будет иметь единственное будет иметь единственное

решение решение

Ответим на поставленный вопрос. Наши решения покажем на координатных прямых.

a

нет два нет

a

решения решения решений

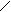
нет одно

решения решение

При a = 1 уравнение имеет одно решение.

Учтем ОДЗ x ≠ – 2; x ≠ –6;

x ≥ –3; x < –3;

x ≠ –6; x ≠ – 2; x ≠ –6; x ≠ – 2;

a ≠ 0;

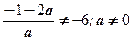
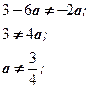
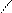
С учетом ОДЗ

a

3/4

a

1/4

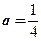При и уравнение имеет одно решение.

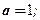
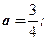
Ответ: 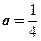- единственное решение.

Решить самостоятельно:

При каких значениях a уравнение имеет единственное решение? Ответ: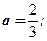

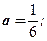
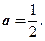
При каких значениях параметра a уравнение имеет два различных корня?

Так как 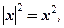то сделав замену где 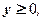получим новое квадратное уравнение

Для того чтобы исходное уравнение имело два различных корня, новое уравнение должно иметь только один положительный корень. Это будет в двух следующих случаях:

а) один из корней положителен, другой отрицателен. Для этого достаточно, чтобы дискриминант был положительным, а произведение корней было отрицательным;

б) оба равных корня положительны. Для этого достаточно, чтобы дискриминант был равен нулю, а сумма корней была положительной.

Таким образом, получим совокупность двух систем.

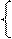1) Д > 0, 2) Д = 0,

y₁ ∙ y₂ < 0; y₁ + y₂ > 0;

Так как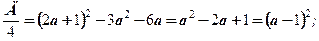

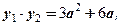то системы будут иметь вид:

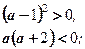
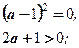
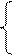
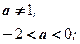
Откуда 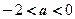или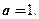

Ответ: ;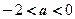

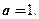
При каких значениях с уравнение x² – ( 3c – 2 ) ∙ | x | + 2c² – c = 0 имеет 4 различных корня?

Так как | x |² = x², то сделав замену | x | = y, где y ≥ 0, получим новое квадратное уравнение y ² – ( 3c – 2 ) ∙ y + 2c² – c = 0.

Для того чтобы исходное уравнение могло иметь четыре различных корня новое уравнение должно иметь два положительных корня. Это будет в том случае, когда дискриминант, произведение и сумма корней будут положительны.

Таким образом, получим систему неравенств:

Д > 0;

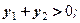
Так как Д = ( 3c – 2 )² – 4∙ ( 2c² – c ) = 9c² – 12c + 4 – 8c² +4c = c² – 8c +4

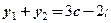
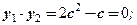то система будет иметь вид:

c² – 8c +4 > 0;

3c – 2 > 0; Откуда имеем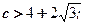

2c² – c > 0;

Ответ: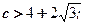

СПИСОК ЛИТЕРАТУРЫ

1. М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич. Сборник задач по алгебре 8-9.Москва, 2000

2. Г.А. Ястребинецкий. Задачи с параметрами. Москва, 1986

3. П.И.Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. Киев, 1992

4. В.В.Ткачук. Математика-абитуриенту,т1.Москва, 1994

5. С.Л.Попцов. Как решать задачи с параметром. Тверь, 1999

6. Сборник задач по математике для поступающих во втузы. Под редакцией М.И. Сканави, Москва, 2003