Дифференциальные уравнения второго порядка
С постоянными коэффициентами
Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид:
 (4.12)
(4.12)
где  - некоторые действительные числа,
- некоторые действительные числа,  - некоторая функция. Мы будем рассматривать однородные уравнения (
- некоторая функция. Мы будем рассматривать однородные уравнения (  ), т. е. уравнения вида
), т. е. уравнения вида
 (4.13)
(4.13)
v Рассмотрим решение линейного однородного уравнения с постоянными коэффициентами.
Для нахождения общего решения однородного уравнения составляем его характеристическое уравнение:
 .
.
Находим его корни. При этом, если:
1. Корни вещественные различные, т.е.  , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
 (4.14)
(4.14)
2. Корни вещественные кратные, т.е.  , то общее решение уравнения имеет вид:
, то общее решение уравнения имеет вид:
 (4.15)
(4.15)
3. Корни комплексные, т.е.  , то общее решение имеет вид:
, то общее решение имеет вид:
 (4.16)
(4.16)
Пример.
 .
.
Решение.
Запишем и решим характеристическое уравнение:
 ,
,
 ,
,  .
.
Тогда общее решение данного уравнения имеет вид:
 .
.
Пример.

Решение.
 ,
,
 ,
,
 - корни кратные, вещественные,
- корни кратные, вещественные,
 - общее решение.
- общее решение.
Пример.
 .
.
Решение.
 ,
,
 ,
,
 - корни комплексные,
- корни комплексные,

 - общее решение.
- общее решение.
V. Числовые ряды
Основные понятия
| Определение 1. | Пусть задана бесконечная последовательность чисел  , тогда выражение , тогда выражение  называется числовым рядом. При этом числа называется числовым рядом. При этом числа  называются членами ряда. называются членами ряда. |
| Определение 2. | Ряд  называется сходящимся, если сумма называется сходящимся, если сумма  его его 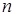 первых членов при первых членов при  стремится к конечному пределу стремится к конечному пределу  : :  . Число . Число  называется суммой сходящегося ряда. Ряд не сходящийся называется расходящимся. называется суммой сходящегося ряда. Ряд не сходящийся называется расходящимся. |
Необходимый признак сходимости ряда Если ряд сходится, то его 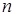 -й член стремится к нулю при неограниченном возрастании
-й член стремится к нулю при неограниченном возрастании 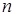 , т.е.
, т.е.
 .
.
| Следствие | Если 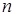 -й член ряда не стремится к нулю при -й член ряда не стремится к нулю при  , то ряд расходится. , то ряд расходится. |
| Замечание | Выполнение необходимого признака сходимости не говорит о том, что ряд сходится. Это следует показать с помощью одного из достаточных признаков. |
Достаточные признаки сходимости
v Признак Даламбера
Если в ряде с положительными членами  отношение
отношение  -го члена к
-го члена к 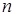 -му при
-му при  имеет предел
имеет предел  , т.е.
, т.е.
 ,
,
то:
1) ряд сходится в случае  ,
,
2) ряд расходится в случае  ,
,
3) вопрос остается нерешенным в случае  .
.
Пример.
Исследовать сходимость ряда  .
.
Решение:

 ,
,  .
.
Тогда:
 ;
;
таким образом, данный ряд сходится.
v Радикальный признак Коши
Если для ряда с положительными членами:
 ,
,
величина  при
при  имеет предел
имеет предел  , т.е.:
, т.е.:
 ,
,
то:
1) ряд сходится в случае  ;
;
2) ряд расходится в случае  ;
;
3) вопрос остается нерешенным в случае  .
.
Пример.
Исследовать на сходимость ряд  .
.
Решение.
 ,
,
тогда:
 .
.
Таким образом, ряд расходится.
v Интегральный признак сходимости ряда
Пусть члены ряда  положительны и не возрастают, а
положительны и не возрастают, а 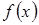 – такая непрерывная не возрастающая функция, что:
– такая непрерывная не возрастающая функция, что:
 .
.
Тогда:
1) ряд сходится, если несобственный интеграл  сходится (равен конечному числу);
сходится (равен конечному числу);
2) ряд расходится, если несобственный интеграл  расходится, т.е. равен
расходится, т.е. равен  , или он не существует (ни конечный, ни бесконечный).
, или он не существует (ни конечный, ни бесконечный).
Пример.
Исследовать сходимость ряда  .
.
Решение.
Применим интегральный признак, положив  . Эта функция удовлетворяет всем условиям признака.
. Эта функция удовлетворяет всем условиям признака.
Рассмотрим интеграл.

т.е. для случая  .
.
 интеграл сходится
интеграл сходится  ряд сходится.
ряд сходится.
Для случая 
 интеграл расходится
интеграл расходится  ряд расходится.
ряд расходится.
v Сравнение рядов с положительными членами
Пусть даны два ряда с положительными членами:
 (5.1)
(5.1)
 , (5.2)
, (5.2)
тогда:
1) если  и ряд (5.2) сходится, то и ряд (5.1) является сходящимся;
и ряд (5.2) сходится, то и ряд (5.1) является сходящимся;
2) если  и ряд (5.2) расходится, то расходится и ряд (5.1).
и ряд (5.2) расходится, то расходится и ряд (5.1).
Пример.
Исследовать на сходимость ряд  .
.
Решение.
Сравним данный ряд с рядом  , члены которого, начиная со второго, образуют геометрическую прогрессию со знаменателем
, члены которого, начиная со второго, образуют геометрическую прогрессию со знаменателем  . Сумма этого ряда равна
. Сумма этого ряда равна  , т.е. он сходящийся. Каждый член исходного ряда меньше соответствующих членов ряда
, т.е. он сходящийся. Каждый член исходного ряда меньше соответствующих членов ряда 
 .
.
Таким образом, исходный ряд сходится, причем его сумма не превосходит  .
.
v Знакочередующиеся ряды. Признак Лейбница
Если в знакочередующемся ряде:
 ,
,
члены таковы, что  и
и  , то ряд сходится, его сумма положительна и не превосходит первого члена.
, то ряд сходится, его сумма положительна и не превосходит первого члена.
Пример.
Исследовать на сходимость ряд  .
.
Решение.
1)  – каждый член ряда по модулю меньше предыдущего;
– каждый член ряда по модулю меньше предыдущего;
2)  , т.о. по признаку Лейбница ряд сходится.
, т.о. по признаку Лейбница ряд сходится.
