Теорема без доказательства

Дать определения монотонной функции четной и нечетной, периодической, ограниченной функций.

1) Монотонная функция — это функция, меняющаяся в одном и том же направлении. Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

2) Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).

3) Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).

4) Периодическая функция ― функция, повторяющая свои значения через какой-то регулярный интервал, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа.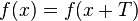

5) Функция называется ограниченной, если существует такое положительное число M, что | f ( x ) | M для всех значений x

Билет 12.

Дать определение предела числовой последовательности; определения бесконеч-но малых (б.м.) и бесконечно больших (б.б.) числовых последовательностей. Рас-сказать о связи б.м. и б.б. числовых последовательностей.

Число а называется пределом числовой последовательности{x_n}, если для любого сколь угодного малого положительного числа £ существует номер n₀такой, что все элементы последовательности с номерами n>n₀удовлетворяющие неравенству |x_n - a|<£.

Число а называется пределом числовой последовательности {x_n}, тогда и только тогда, когда вне любой £-окрестности точки а находится лишь конечное число элементов этой последовательности

Если предел числовой последовательности конечный, то последовательность называется сходящейся. Если предел числовой последовательности бесконечный или не существует называется расходящейся.

Бесконечно малая числовая последовательность – это последовательность, предел которой равен нулю.

Х_n = 1/n, n = 1,2…. – является бесконечно малой.

Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.

{X_n} = ∞

Связь бесконечно малой и большой числовой последовательности.

Теорема без доказательства.

Если {X_n} – бесконечно большая последовательность, то {1/X_n} является бесконечно малой последовательностью ¹/_{бесконечность}→ 0; Если {X_n} – бесконечно малая последовательность и все элементы последовательности отличны от 0, то последовательность {1/X_n} является бесконечно большой последовательностью ¹/_→0→∞.

которой равен произведению пределов последовательностей u.

Билет 17.

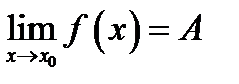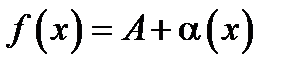Дать определения б.м. и б.б. функций. Доказать, что если , то , где 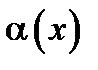– б.м. функция при .

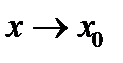Функция y=f(x) называется б.м. при х→х₀, если limf(x)=0. Функция y=f(x) называется б.б. при х→х₀, если limf(x)=∞.

Если функция y=f(x) имеет конечный предел равны: А при х→х₀, то ее можно представить в виде суммы этого предела и бесконечно малой функции. Другими словами, если функция при х→х₀.

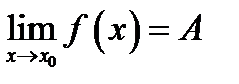{f(x) = A+α(x), limα(x)=0}.

Доказательство. По условию теоремы - 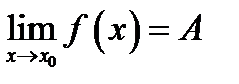. Обозначим|f(x)-A|=α(x). limα(x)=0, то есть α(х) – является бесконечно малой при х→х₀.

Итак: f(x) – A = α(x); limα(x)=0, то есть f(x) =A + α(x), где α(х) – является бесконечно малая функция.

Билет 20.