Методические приложения к контрольной работе.
УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛИПЕЦКОЙ ОБЛАСТИ
ГОАПОУ «Липецкий металлургический колледж»

| Методические указания по выполнению контрольной работы по дисциплине ЕН 01 «Математика» |
| Контрольная работа | ||
| для специальности (группы специальностей): | ||
| 38.02.01 Экономика и бухгалтерский учет (по отраслям), 38.02.03 Операционная деятельность в логистике, 22.02.01 Металлургия черных металлов, 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям), 15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям) | ||
Липецк-2015
Методические указания по выполнению контрольной работы по
дисциплине ЕН 01«Математика» для специальностей 38.02.01 Экономика и бухгалтерский учет (по отраслям), 38.02.03 Операционная деятельность в логистике, 22.02.01 Металлургия черных металлов, 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям), 15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
Составитель: Ланина Ю.А., преподаватель математических дисциплин
| ОДОБРЕНО Цикловой комиссией МОЕНД Председатель: _______________ /Красникова Л.Н./ | Заместитель директора по учебной работе: _________________/Перкова Н. И./ |
Введение
Методические указания по выполнению контрольной работы разработаны согласно рабочим программам ЕН 01 «Математика» для специальностей 38.02.01 Экономика и бухгалтерский учет (по отраслям), 38.02.03 Операционная деятельность в логистике, 22.02.01 Металлургия черных металлов, 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям), 15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям) заочного отделения по дисциплине «Математика».
Выполнение контрольной работы направлено на овладение следующими знаниями и умениями.
В результате освоения дисциплины обучающийся должен уметь:
- анализировать сложные функции и строить их графики;
- выполнять действия над комплексными числами;
- вычислять значения геометрических величин;
- производить операции над матрицами и определителями;
- решать задачи на вычисление вероятности с использованием элементов комбинаторики;
- решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений;
- решать системы линейных уравнений различными методами.
В результате освоения дисциплины обучающийся должен знать:
- основные математические методы решения прикладных задач;
- основные понятия и методы математического анализа, линейной алгебры, теорию комплексных чисел, теории вероятностей и математической статистики;
- основы интегрального и дифференциального исчисления;
- роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности.
Вариант контрольной работы выбирается по последней цифре в журнале.
Номера задач указаны в таблице, где в первом столбце по вертикали стоит последняя цифра вашего варианта.
При выполнении контрольной работы необходимо соблюдать следующие правила:
1. Работа выполняется в отдельной тетради, на обложке которой указывается учебная дисциплина, номер варианта, Ф.И.О.
2. Условия задачи необходимо записывать полностью. К геометрическим задачам делается чертёж.
3. Решения задач должны сопровождаться краткими, но достаточными объяснениями. Для решения выбирать оптимальный вариант.
4. Проверенные работы сохраняются и предоставляются на зачете.
5. Студент должен ознакомиться с рецензией преподавателя и дать объяснения по все замечаниям, чтобы быть готовым к защите работы.
6. Если работа не зачтена, то её необходимо переделать и сдать на повторную рецензию.
7. Основной материал, изучается по учебникам.
Методические приложения к контрольной работе.
Векторы.

 Отрезок, для которого указано, какой из его концов считается началом, а какой - концом, называется направленным отрезком или вектором.
Отрезок, для которого указано, какой из его концов считается началом, а какой - концом, называется направленным отрезком или вектором.
 Вектор обозначается: , АВ , где А – начало вектора, В – конец вектора.
Вектор обозначается: , АВ , где А – начало вектора, В – конец вектора.
Векторы называются равными, если они сонаправлены и их длины равны, т.е.
 если
если  и
и 
Расстояние  называется длиной вектора или модулем вектора. Если вектор задан своими координатами
называется длиной вектора или модулем вектора. Если вектор задан своими координатами  , то
, то  . Длина вектора
. Длина вектора  =
=  , если
, если  и
и  .
.
Действия над векторами, заданными своими координатами.
Пусть даны  и
и  , тогда:
, тогда:



Cкалярнымпроизведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
 или
или

Произведение применяется в физике и механике.
Проекция вектора 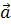 на вектор
на вектор 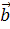 находится по формуле:
находится по формуле:
 ,
,  - угол между векторами
- угол между векторами  .
.
Угол между векторами находится по формуле:

Деление отрезка в данном отношении. Координаты точки деления С отрезка АВ в отношении  вычисляются по формулам:
вычисляются по формулам:
 ;
; 
Примеры:
1.Найти проекцию вектора 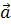 на вектор
на вектор 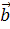 ,если угол между ними равен
,если угол между ними равен 
 .
.
Решение. 
2.Найти длину вектора  , если
, если  ,
,  .
.
Решение. По формуле  =
=  , находим
, находим
 =
= 
3.Найти модуль вектора  , если
, если  .
.
Решение.3 



Метод координат.
Пример. Даны вершины треугольника АВС: А(1;-1), В(-2;1), С(3;5)
1)Вычислить: 
2)Составить уравнения сторон 
3)Вычислить длину медианы ВЕ и величину угла А.
4)Сделать чертеж
Решение. 1.Найдём координаты векторов  по формуле:
по формуле:



2.Длину вектора вычислим по формуле: 
Получим: 

3.Найдем скалярное произведение  , по формуле
, по формуле

 , здесь (-2; -6) координаты вектора
, здесь (-2; -6) координаты вектора  .
.
4.Уравнения сторон ВС и СА составим, воспользовавшись уравнением прямой, проходящей через две заданные точки:

Уравнение прямой ВС:  ;
;  ;
;
4(х+2)=5(у-1) 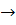 4х+8=5у-5
4х+8=5у-5 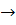 4х-5у+13=0
4х-5у+13=0
Уравнение прямой АС:  ;
; 
6(х-1)=2(у+1) 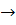 6х-6=2у+2
6х-6=2у+2 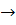 6х-2у-8=0
6х-2у-8=0
5.Найдём длину медианы ВЕ.
Так как медиана делит противоположную сторону АС пополам, то координаты точки Е, найдем, как координаты середины отрезка
 и
и 

 т.е. Е (2;2)
т.е. Е (2;2)
Длину медианы найдем по формуле: 

6.Найдем величину косинуса угла А ,


