В а р и а н т ы з а д а н и й 1-13
| 1. | А(–2;1;1); | В(–5;1;–2); | С(–3;0;3); | D(–6;0;1). |
| 2. | А(–3;–4;1); | В(–2;–3;–5); | С(0;0;0); | D(–6;0;3). |
| 3. | А(–2;4;5); | В(1;3;–4); | С(–5;–5;1); | D(–1;2;–2). |
| 4. | А(–1;2;0); | В(–4;2;–3); | С(–2;1;2); | D(–5;1;0). |
| 5. | А(–2;–3;0); | В(–1;–2;–6); | С(1;1;–1); | D(–5;1;2). |
| 6. | А(–1;5;–6); | В(2;4;–5); | С(–4;–4;0); | D(0;3;–3). |
| 7. | А(–3;2;2); | В(–6;2;–1); | С(–4;1;4); | D(–7;1;2). |
| 8. | А(–4;–3;2); | В(–3;–2;–4); | С(–1;1;1); | D(–7;1;4). |
| 9. | А(–3;5;–4); | В(0;4;–3); | С(–6;–4;2); | D(–2;3;–1). |
| 10. | А(0;1;1); | В(–3;1;–2); | С(–1;0;3); | D(–4;0;1). |
| 11. | А(1;–2;1); | В(1;–5;–2); | С(0;–3;3); | D(0;–6;1). |
| 12. | А(–4;–3;1); | В(–3;–2;–5); | С(0;0;0); | D(0;–6;3). |
| 13. | А(4;–2;–5); | В(3;1;–4); | С(–5;–5;1); | D(2;–1;–2). |
| 14. | А(2;–1;0); | В(2;–4;–3); | С(1;–2;2); | D(1;–5;0). |
| 15. | А(–3;–2;0); | В(–2;–1;–6); | С(1;1;–1); | D(1;–5;2). |
| 16. | А(5;–1;–6); | В(4;2;–5); | С(–4;–4;0); | D(3;0;–3). |
| 17. | А(2;–3;2); | В(2;–6;–1); | С(1;–4;4); | D(1;–7;2). |
| 18. | А(–3;–4;2); | В(–2;–3;–4); | С(1;–1;1); | D(1;–7;4). |
| 19. | А(5;–3;–4); | В(4;0;–3); | С(–4;–6;2); | D(3;–2;–1). |
| 20. | А(1;0;1); | В(1;–3;–2); | С(0;–1;3); | D(0;–4;1). |
| 21. | А(1;0;1); | В(–2;1;–5); | С(3;0;–3); | D(1;0;–6). |
| 22. | А(1;–4;–3); | В(–5;–3;–2); | С(0;0;0); | D(3;0;–6). |
| 23. | А(–5;4;–2); | В(–4;3;1); | С(1;–5;–5); | D(–2;2;–1). |
| 24. | А(0;2;–1); | В(–3;2;–4); | С(2;1;–2); | D(0;1;–5). |
| 25. | А(0;–3;–2); | В(–6;–2;–1); | С(–1;1;1); | D(2;1;–5). |
| 26. | А(–6;5;–1); | В(–5;4;2); | С(0;–4;–4); | D(–3;3;0). |
| 27. | А(2;2;–3); | В(–1;2;–6); | С(4;1;–4); | D(2;1;–7). |
| 28. | А(2;–3;–4); | В(–4;–2;–3); | С(1;1;–1); | D(4;1;–7). |
| 29. | А(–4;5;–3); | В(–3;4;0); | С(2;–4;–6); | D(–1;3;–2). |
| 30. | А(1;1;0); | В(–2;1;–3); | С(3;0;–1); | D(1;0;–4). |
Задание 14.
Методом сечений определить вид поверхности. Сделать чертеж.
В А Р И А Н Т Ы З А Д А Н И Я 14
1.x2 – 4y2 + 4z2 = 16. 2.4x2 – 12y + 3z2 = 0.
3.x2 + 2y2 + 3z2 = 18. 4.4x2 – y2 – z2 = 4.
5.16x2 + 9y2 – 4z2 = 0. 6.3x2 + 4y2 – 12z = 0.
7.5x2 + 5y2 – 4z2 = 20. 8.9x2 – y2 – z2 = 9.
9.x2 + 4y2 + 2z2 = 4. 10.9x2 – 4y2 + 9z2 = 0.
11.x2 – 16y2 – z2 = 16. 12.4x2 + 3y2 – 6z2 = 0.
13.4x2 + 3y2 + 4z2 = 12. 14.–9x2 + 9y2 + 4z2 = 0.
15.x2 – y2 – 2z = 0. 16.x2 + y2 = 4.
17.x2 + y2 – 8z = 0. 18.4x2 – 4z2 = 16.
19.16x2 + y2 – z2 = 16. 20.y2 - 4z = 0.
21.4x2 – y2 = 0. 22.–x2 + 16y2 – z2 = 16.
23.4y2 – z2 = 8x. 24.2z2 – 5 = 0.
25.9x2 – 4y2 = 36. 26.4x2 – 4y2 + z2 = 16.
27.4x2 + 3y2 – 12z = 0. 28.–x2 – 16y2 + z2 = 16.
29.x2 + z2 = 9. 30.x2 – 4y2 = 0.
Задание 15.
Выделением полных квадратов и переносом начала координат привести уравнение поверхности к канонической форме и определить ее вид.
В А Р И А Н Т Ы З А Д А Н И Я 15
1.x2 + y2 + z2 – 4x + 8y – 6z + 20 = 0.
2.4x2 + y2 – 8z2 + 8x – 4y + 16z – 32 = 0.
3.9x2– 4y2 – 36z2 –18x–16y–216z – 367=0.
4.3x2 + y2 + 2z2 – 12x – 6y + 4z – 13 = 0.
5.2x2 – 3z2 + 4x + 2y + 6z + 1 = 0.
6.x2 + 4y2 – 9z2 – 2x – 16y – 18z + 45 = 0.
7.2x2 + 3y2 + 12x – 12y – 18z + 30 = 0.
8.y2 – 8x – 2y +4 = 0.
9.4x2 – 6y2 + 9z2 + 24x + 12y +36z+30 = 0.
10.3x2 + 2y2 + 4z2 + 18x – 4y – 16z +33 = 0.
11.2x2 + 3y2 – 4x + 6y – 12z + 14 = 0.
12.8x2 – 6y2 – 3z2 + 16x – 12y + 18z–49 = 0.
13.20x2+15y2–12z2–120x+30y+72z+87 = 0.
14.4x2 + 6y2 + 9z2 + 24x – 12y –36z+42 = 0.
15.3x2 + 4y2 – 6x – 56y + 187 = 0.
16.x2 + y2 + z2 + 6x – 2y – 4z – 2 = 0.
17.3y2 – 4z2 – 6y + 56z – 205 = 0.
18.2y2 – 3z2 – 12x – 4y – 6z – 10 = 0.
19.2x2 – 3y2 – 4x – 6y – 12z – 10 = 0.
20.4x2 + 6y2 – 9z2 + 8x – 12y + 54z – 107 = 0.
21.3x2 – 4y2 – 6x + 56y – 205 = 0.
22.8x2 – 6y2 + 3z2 + 16x + 12y – 18z + 5 = 0.
23.20x2–15y2+12z2–120x–30y–72z+273=0.
24.–4x2– 6y2 + 9z2 – 8x + 12y–54z + 35 = 0.
25.2y2 + 3z2 – 12x – 4y + 6z + 14 = 0.
26.x2 + y2 + z2 + 8x – 4y – 6z + 20 = 0.
27.x2 – 9y2 + 4z2 – 2x – 18y – 16z + 45 = 0.
28.3y2 + 2z2 – 12x + 6y – 4z + 14 = 0.
29.x2 + y2 + z2 + 6x – 4y – 2z – 2 = 0.
30.3x2 – 4z2 – 6x + 56z – 205 = 0.
Раздел 2. ЛИНЕЙНАЯ АЛГЕБРА
ТИПОВОЙ РАСЧЕТ № 3
Задание 1.
Вычислить определители матриц А и В.
В А Р И А Н Т Ы З А Д А Н И Я 1
1.а) 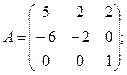 б)
б) 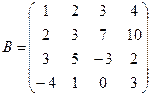 .
.
2.а) 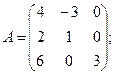 б)
б) 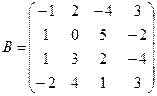 .
.
3.а) 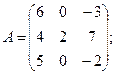 б)
б) 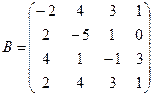 .
.
4.а) 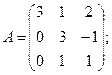 б)
б) 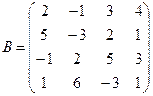 .
.
5.а) 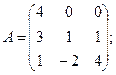 б)
б) 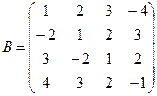 .
.
6.а) 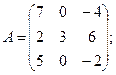 б)
б) 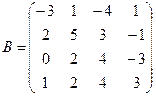 .
.
7.а) 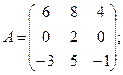 б)
б) 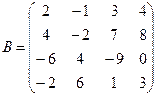 .
.
8.а) 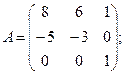 б)
б) 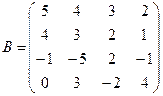 .
.
9.а) 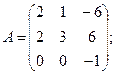 б)
б) 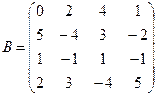 .
.
10.а) 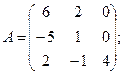 б)
б) 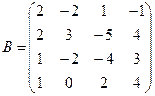 .
.
11.а) 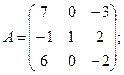 б)
б) 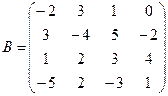 .
.
12.а) 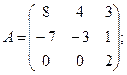 б)
б) 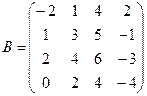 .
.
13.а) 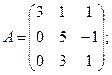 б)
б) 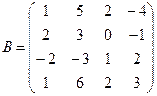 .
.
14.а) 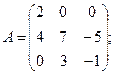 б)
б) 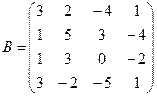 .
.
15.а) 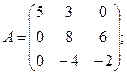 б)
б) 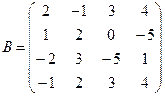 .
.
16.а) 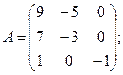 б)
б) 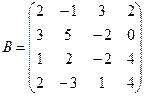 .
.
17.а) 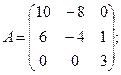 б)
б) 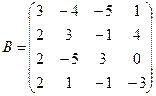 .
.
18.а) 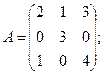 б)
б) 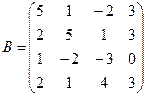 .
.
19.а) 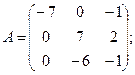 б)
б) 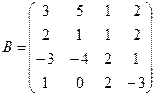 .
.
20.а) 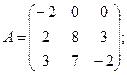 б)
б) 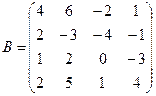 .
.
21.а) 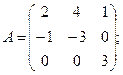 б)
б) 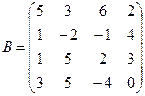 .
.
22.а) 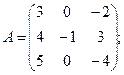 б)
б) 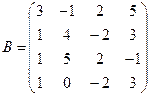 .
.
23.а) 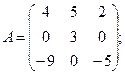 б)
б) 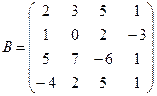 .
.
24.а) 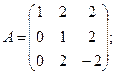 б)
б) 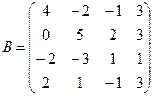 .
.
25.а) 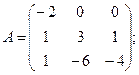 б)
б) 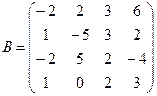 .
.
26.а) 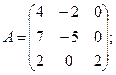 б)
б) 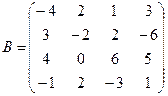 .
.
27.а) 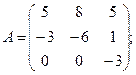 б)
б) 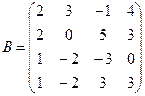 .
.
28.а) 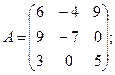 б)
б) 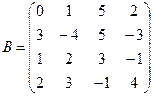 .
.
29.а) 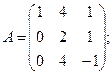 б)
б) 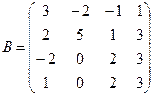 .
.
30.а) 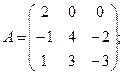 б)
б) 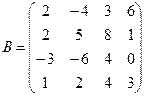 .
.
Задание 2.
Для данных матриц A и B указать, какие из приведенных операций выполнимы, и выполнить их: 1) A + B; 2) AT+ B; 3) A + B T; 4) AT+ B T; 5) AB; 6) ATB; 7) AB T; 8) BAT.
В А Р И А Н Т Ы З А Д А Н И Я 2
1. 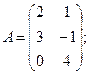
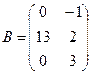 .
.
2. 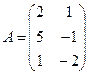 ;
; 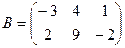 .
.
3. 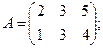
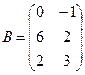 .
.
4. 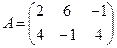 ;
; 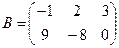 .
.
5. 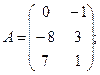
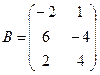 .
.
6. 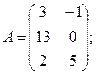
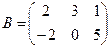 .
.
7. 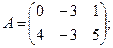
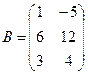 .
.
8. 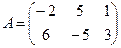 ;
; 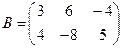 .
.
9. 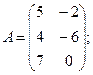
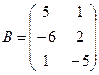 .
.
10. 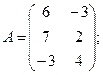
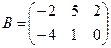 .
.
11. 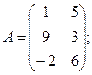
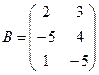 .
.
12. 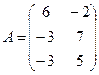 ;
; 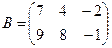 .
.
13. 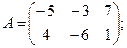
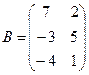 .
.
14. 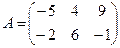 ;
; 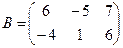 .
.
15. 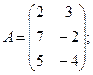
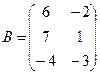 .
.
16. 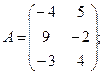
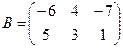 .
.
17. 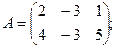
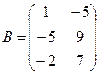 .
.
18. 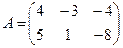 ;
; 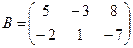
19. 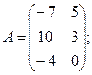
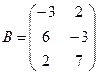 .
.
20. 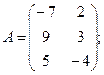
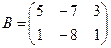
21. 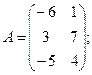
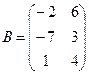 .
.
22. 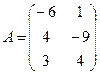 ;
; 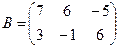 .
.
23. 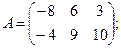
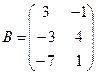 .
.
24. 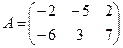 ;
; 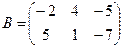 .
.
25. 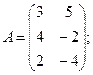
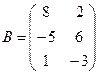 .
.
26. 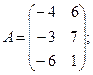
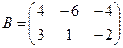 .
.
27. 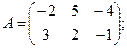
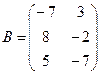 .
.
28. 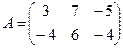 ;
; 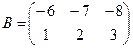
29. 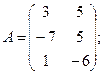
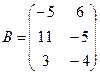 .
.
30. 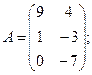
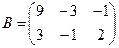 .
.
Задание 3.
Для данной матрицы А найти обратную, если она существует, и установить, что АА-1 = Е.
В А Р И А Н Т Ы З А Д А Н И Я 3
1. 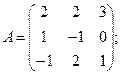 2.
2. 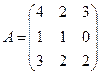 ;
;
3. 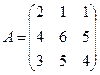 ; 4.
; 4. 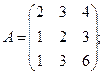
5. 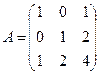 ; 6.
; 6. 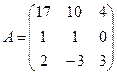 ;
;
7. 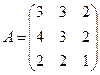 ; 8.
; 8. 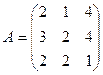 ;
;
9. 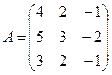 ; 10.
; 10. 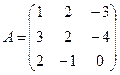 ;
;
11. 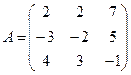 ; 12.
; 12. 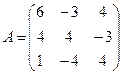 ;
;
13. 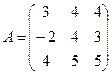 ; 14.
; 14. 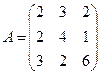 ;
;
15. 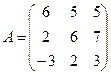 ; 16.
; 16. 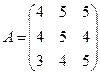 ;
;
17. 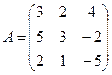 ; 18.
; 18. 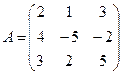 ;
;
19. 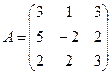 ; 20.
; 20. 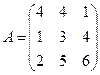 ;
;
21. 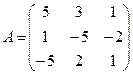 ; 22.
; 22. 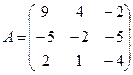 ;
;
23. 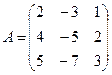 ; 24.
; 24. 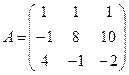 ;
;
25. 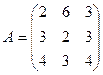 ; 26.
; 26. 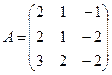 ;
;
27. 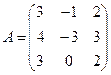 ; 28.
; 28. 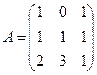 ;
;
29. 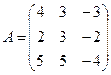 ; 30.
; 30. 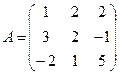 .
.
Задание 4.
Решить систему уравнений 1)методом Крамера; 2)в матричной форме.
В А Р И А Н Т Ы З А Д А Н И Я 4
1. 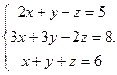 2.
2. 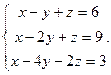
3. 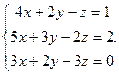 4.
4. 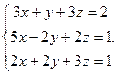
5. 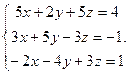 6.
6. 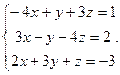
7. 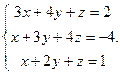 8.
8. 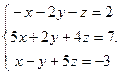
9. 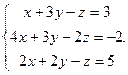 10.
10. 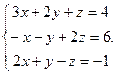
11. 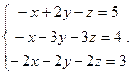 12.
12. 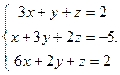
13. 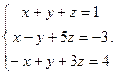 14.
14. 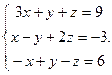
15. 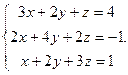 16.
16. 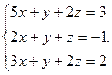
17. 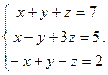 18.
18. 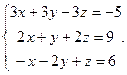
19. 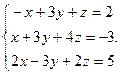 20.
20. 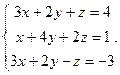
21. 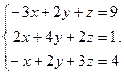 22.
22. 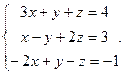
23. 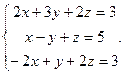 24.
24. 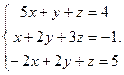
25. 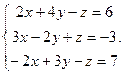 26.
26. 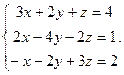
27. 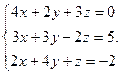 28.
28. 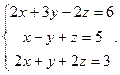
29. 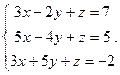 30.
30. 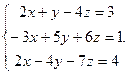
Задание 5.
Сравнить ранги основной и расширенной матриц системы уравнений, сделать вывод и решить систему методом Гаусса.
В А Р И А Н Т Ы З А Д А Н И Я 5
1. 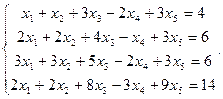
2. 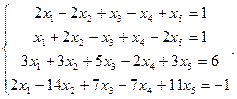
3. 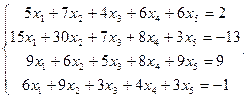
4. 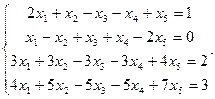
5. 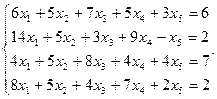
6. 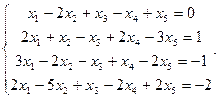
7. 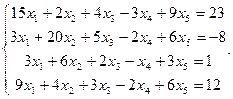
8. 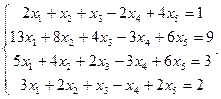
9. 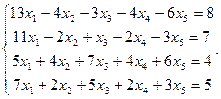
10. 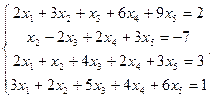
11. 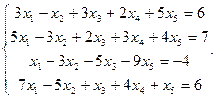
12. 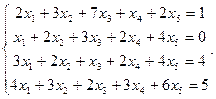
13. 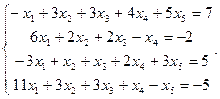
14. 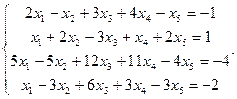
15. 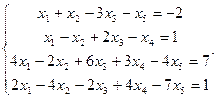
16. 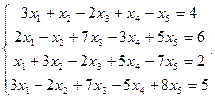
17. 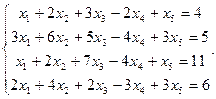
18. 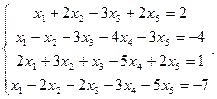
19. 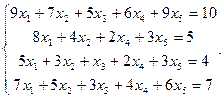
20. 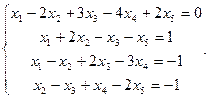
21. 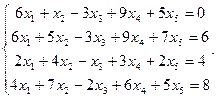
22. 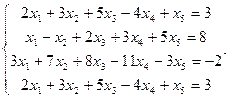
23. 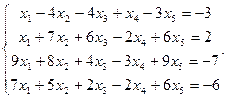
24. 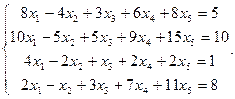
25. 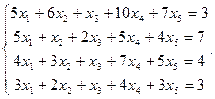
26. 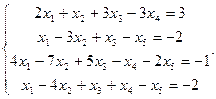
27. 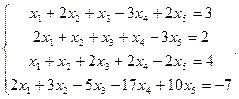
28. 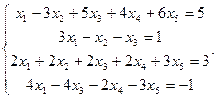
29. 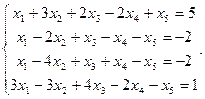
30. 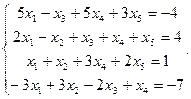
Задание 6.
Найти собственные значения и собственные векторы матрицы.
В А Р И А Н Т Ы З А Д А Н И Я 6
1. 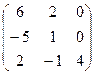 2.
2. 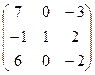 3.
3. 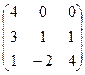
4. 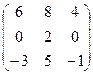 5.
5. 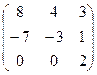 6.
6. 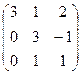
7. 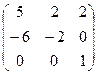 8.
8. 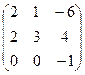 9.
9. 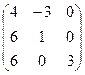
10. 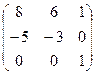 11.
11. 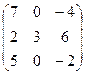 12.
12. 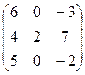
13. 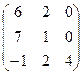 14.
14. 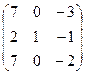 15.
15. 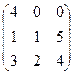
16. 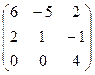 17.
17. 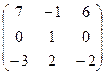 18.
18. 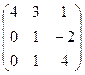
19. 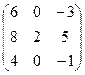 20.
20. 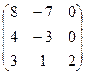 21.
21. 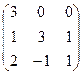
22. 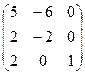 23.
23. 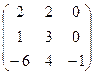 24.
24. 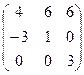
25. 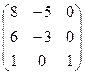 26.
26. 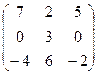 27.
27. 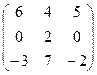
28. 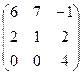 29.
29. 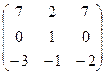 30.
30. 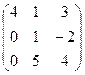
Задание 7.
Определить, являются ли линейно зависимыми данные векторы.
В А Р И А Н Т Ы З А Д А Н И Я 7
| 1. | (3;2;4;7); | (4;–3;11;–2) | (–5;3;–13;1) | (7;–2;16;3). |
| 2. | (1;1;4;2); | (1;1;–2;4); | (0;2;6;–2); | (–3;–1;3;4). |
| 3. | (2;3;5;2); | (1;–2;1;–1); | (–1;2;–1;1); | (1;–3;2;–3). |
| 4. | (1;0;1;0); | (–2;1;3;–7); | (3;–1;0;3); | (4;–3;1;–3). |
| 5. | (1;2;3;1); | (2;3;1;2); | (3;1;2;–2); | (0;4;2;5). |
| 6. | (2;3;4;1); | (–1;1;–1;3); | (3;–5;1;–13) | (3;0;3;–6). |
| 7. | (1;2;3;-4); | (2;–1;2;5); | (2;–1;5;–4); | (2;3;–4;1). |
| 8. | (2;3;4;1); | (3;–1;1;–2); | (–1;2;–3;4); | (5;–7;6;–7). |
| 9. | (1;2;1;1); | (1;1;1;2); | (–3;–2;1;–3) | (–1;1;3;1). |
| 10. | (1;2;3;4); | (2;3;4;1); | (3;4;1;2); | (7;11;11;11). |
| 11. | (–1;–1;0;2); | (1;0;–1;–2); | (–1;–3;1;5); | (1;2;–3;–6). |
| 12. | (2;1;1;2); | (1;3;1;3); | (1;1;5;3); | (2;5;–7;14). |
| 13. | (–5;3;–13;1); | (7;–2;16;3); | (3;2;4;7); | (4;–3;11;–2). |
| 14. | (0;2;6;–2); | (–3;–1;3;4); | (1;1;4;2); | (1;1;–2;4). |
| 15. | (–1;2;–1;1); | (1;–3;2;–3); | (2;3;5;2); | (1;–2;1;–1). |
| 16. | (3;–1;0;3); | (4;–3;1;–3); | (1;0;1;0); | (–2;1;3;–7). |
| 17. | (3;1;2;–2); | (0;4;2;5); | (1;2;3;1); | (2;3;1;2). |
| 18. | (2;–1;5;–4); | (2;3;–4;1); | (1;2;3;–4); | (2;–1;2;5). |
| 19. | (–1;2;–3;4); | (5;–7;6;–7); | (2;3;4;1); | (3;–1;1;–2). |
| 20. | (–3;–2;1;–3); | (–1;1;3;1); | (1;2;1;1); | (1;1;1;2). |
| 21. | (3;4;1;2); | (7;11;11;11) | (1;2;3;4); | (2;3;4;1). |
| 22. | (–1;–3;1;5); | (1;2;–3;–6); | (–1;–1;0;2); | (1;0;–1;–2). |
| 23. | (1;1;5;3); | (2;5;–7;14); | (2;1;1;2); | (1;3;1;3). |
| 24. | (3;–5;1;–13); | (3;0;3;–6); | (2;3;4;1); | (–1;1;–1;3). |
| 25. | (7;–2;16;3); | (4;–3;11;–2) | (–5;3;–13;1); | (3;2;4;7). |
| 26. | (–3;–1;3;4); | (1;1;–2;4); | (0;2;6;–2); | (1;1;4;2). |
| 27. | (1;–3;2;–3); | (1;–2;1;–1); | (–1;2;–1;1); | (2;3;5;2). |
| 28. | (4;–3;1;–3); | (–2;1;3;–7); | (3;–1;0;3); | (1;0;1;0). |
| 29. | (0;4;2;5); | (2;3;1;2); | (3;1;2;–2); | (1;2;3;1). |
| 30. | (3;0;3;–6); | (–1;1;–1;3); | (3;–5;1;–13) | (2;3;4;1). |
Задание 8.
Найти фундаментальный набор решений системы уравнений.
В А Р И А Н Т Ы З А Д А Н И Я 8
1. 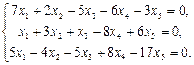
2. 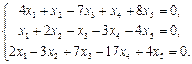
3. 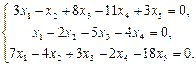
4. 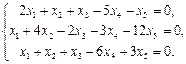
5. 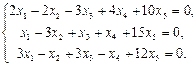
6. 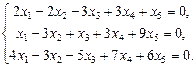
7. 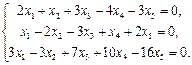
8. 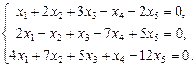
9. 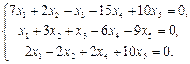
10. 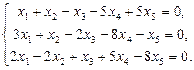
11. 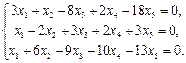
12. 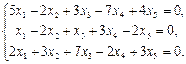
13. 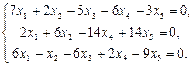
14. 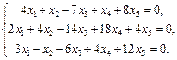
15. 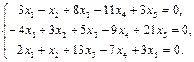
16. 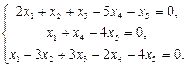
17. 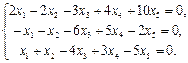
18. 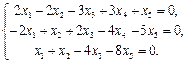
19. 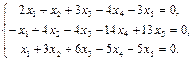
20. 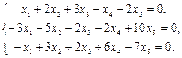
21. 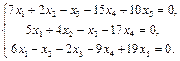
22. 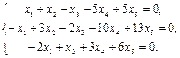
23. 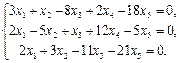
24. 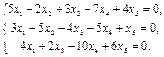
25. 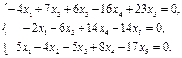
26. 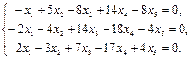
27. 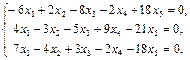
28. 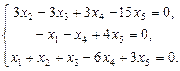
29. 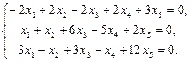
30. 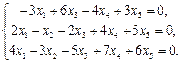
Задание 9.
Найти ортогональный базис линейной оболочки данных векторов.
