Экстраполяция в рядах динамики и прогнозирование
Необходимым условием регулирования рыночных отношений является составление надежных прогнозов развития социально-экономических явлений.
Выявление и характеристика трендов и моделей взаимосвязи создают базу для прогнозирования, т.е. для определения ориентировочных размеров явлений в будущем. Для этого используют метод экстраполяции.
Под экстраполяцией понимают нахождение уровней за пределами изучаемого ряда, т.е. продление в будущее тенденции, наблюдавшейся в прошлом (перспективная экстраполяция). Поскольку в действительности тенденция развития не остается неизменной, то данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятностные оценки.
Экстраполяцию рядов динамики осуществляют различными способами, например, экстраполируют ряды динамики выравниванием по аналитическим формулам. Зная уравнение для теоретических уровней и подставляя в него значения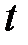 
за пределами исследованного ряда, рассчитывают для 
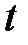вероятностные 
.
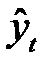Так, по данным таблицы 7.14, на основе исчисленного ранее уравнения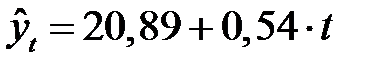 
экстраполяцией при 
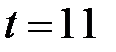можно определить ожидаемую урожайность зерновых культур в 2009 г., ц/га:
.
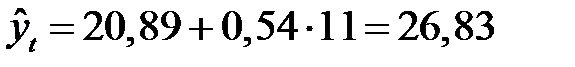На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками.
Для определения границ интервалов используют формулу:
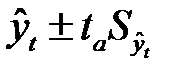, (7.18)
где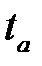 
- коэффициент доверия по распределению Стьюдента;
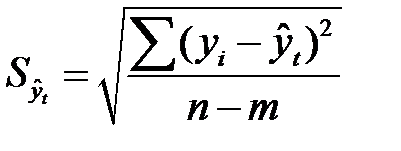- остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы ( 
);
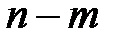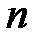- число уровней ряда динамики;
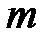- число параметров адекватной модели тренда (для уравнения прямой 
).
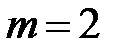Вероятностные границы интервала прогнозируемого явления:
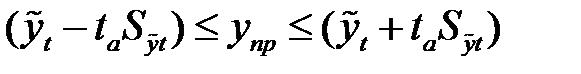. (7.19)
Рассчитаем прогнозируемые доверительные интервалы урожайности зерновых культур на 2009 г.
Есл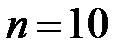и 
и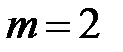 
, то число степеней свободы равно 8. Тогда при доверительной вероятности, равной 0,95 (т.е. при уровне значимости случайностей 
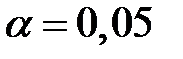коэффициент доверия 
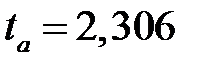(по таблице Стьюдента), 
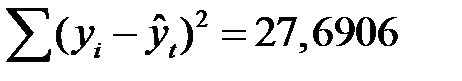(см. таблицу 7.14).
Тогда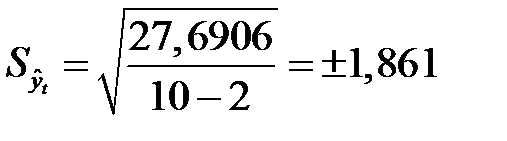 
.
Зная точечную оценку прогнозируемого значения урожайности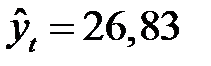 
ц/га, определяем вероятностные границы интервала по формуле (7.19):
,
.
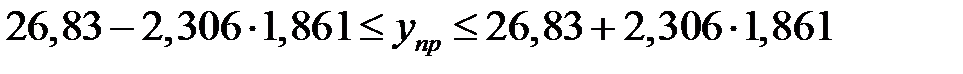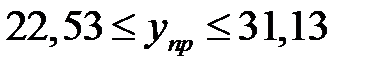Следовательно, с вероятностью, равной 0,95, можно утверждать, что урожайность зерновых культур в 2009 г. не менее чем 22,53, но и не более чем 31,13 ц/га.
Нужно иметь в виду, что экстраполяция в рядах динамики носит не только приближенный, но и условный характер. Поэтому ее следует рассматривать как предварительный этап в разработке прогнозов.