Оболочки, составленные из изотропных слоев.

Пусть оболочка составлена из различных изотропных слоев. В этом случае для упругих постоянных 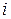-го слоя оболочки имеем

(2.49)

, ,

,

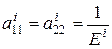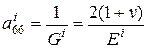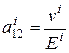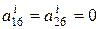
Для коэффициентов 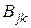имеем

(2.50)

, ,

, .

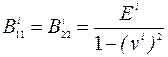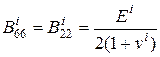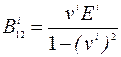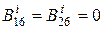Основные напряжения в слоях оболочки определяются из выражений

,

(2.51)

,

.

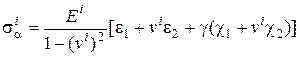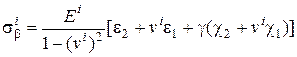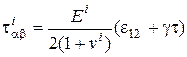При этом

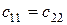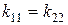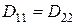, , . (2.52)

Формулы внутренних усилий и выражений потенциальной энергии остаются без изменений, причем надо учитывать лишь новые значения жесткостей.

Здесь неизменными также остаются выражения для деформаций и изменений кривизны, кручения, уравнения равновесия и неразрывности деформаций.

Оболочки, составленные из трансверсально изотропных слоев

Рассмотрим три случая

а) Пусть главные направления упругости в каждой точке каждого слоя совпадают с направлениями координатных линий 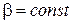. В этом случае надо пользоваться соотношениями, данными для оболочки, составленной из ортотропных слоев, при этом надо полагать для каждого слоя

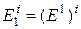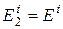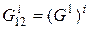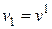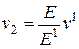, , , , . (2.53)

б) Пусть главные направления упругости в каждой точке слоев совпадают с направлениями координатных линий 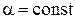. В этом случае также надо пользоваться соотношениями для ортотропной оболочки, причем

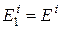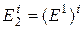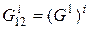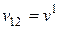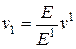, , , , . (2.54)

в) Главные направления упругости в каждой точке слоев нормальны к координатной поверхности оболочки. В этом случае надо пользоваться соотношениями для оболочки, составленной из различных изотропных слоев, при этом надо полагать

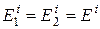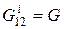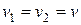, , . (2.55)

Оболочки, составленные из нечетного числа слоев, симметрично расположенных относительно координатной поверхности

Рассмотрим оболочки, составленные из нечетного числа 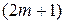однородных анизотропных слоев. Слои оболочки имеют одинаковые толщины и физико-механические свойства. Координатная поверхность является срединной поверхностью как для среднего слоя, так и всей оболочки в целом.

В силу симметрии имеем (см. рис. 2.4)

(2.56)

, ,

, .

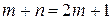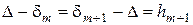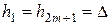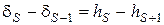При этом из (2.29) для жесткостей оболочки получим

;

(2.57)

;

.

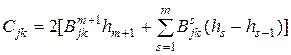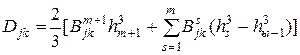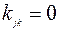Для соотношений упругости и потенциальной энергии соответственно получим

; ;

(2.58)

;

;

; ;

.

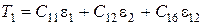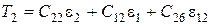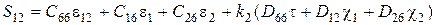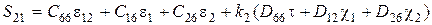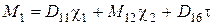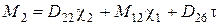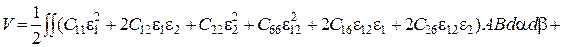
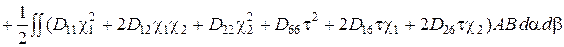. (2.59)

В каждом конкретном случае в эти выражения необходимо подставлять те или иные выражения для жесткостей оболочки.

О соотношениях упругости

Исходя из гипотезы недеформируемых нормалей, следует, что независимо от расположения координатной поверхности оболочки все внутренние силы и моменты в общем случае зависят от деформаций удлинений и сдвига, так и от параметров изменений кривизны ее координатной поверхности.

В связи с этим, безразлично, какое расположение имеет исходная координатная поверхность оболочки. Поэтому интересно выяснить то расположение координатной поверхности оболочки, для которого все жесткости взаимного влияния 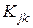превращаются в нуль, и для многослойной оболочки получаются наиболее простые соотношения упругости.

Полагая 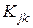=0, из (2.29) получим

при 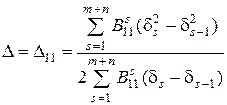, 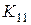=0 (2.60)

при 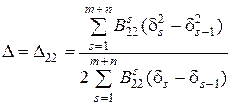, 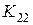=0 (2.61)

при 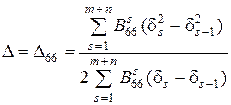, 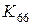=0 и т.д. (2.62)

Рассматривая эти выражения, замечаем, что в общем случае анизотропии слоев оболочки все значения 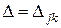отличны друг от друга. Отсюда следует, что в общем случае анизотропной слоистой оболочки, когда не ставятся какие-либо ограничения на упругие характеристики материалов слоев оболочки, нет единого расположения координатной ее поверхности, для которого все жесткости взаимного влияния 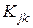превращаются в нуль.

При единой координатной поверхности оболочки все жесткости взаимного влияния 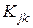превратятся в нуль, если поставить условие

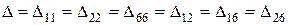, (2.63)

но это условие ставит существенные ограничения на другие характеристики материалов слоев оболочки.

Для примера рассмотрим двухслойную оболочку (рис. 2.6)

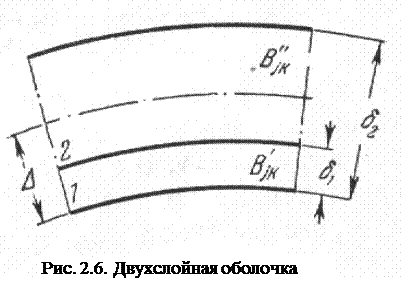Рис.2.6

Полагая 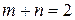, , 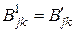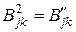из (2.63) получим

= = …

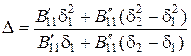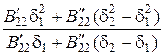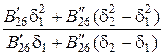= . (2.64)

Отсюда следует, что равенства (2.64) будут иметь место, если

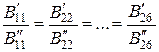, (2.65)

что является существенным ограничением для поставленной задачи.

В частном случае изотропной оболочки из (2.45) для упругих характеристик слоев имеем

(2.66)

, , ,

, , ,

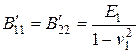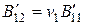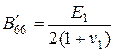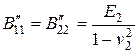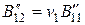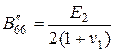где 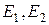– модули упругости соответственно первого и второго слоев;

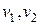– коэффициенты Пуассона первого и второго слоев.

Подставляя 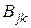из (2.66) в (2.65), получим

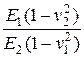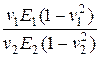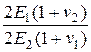= = (2.67)

Отсюда следует, что эти равенства имеют место лишь при условии равенства коэффициентов Пуассона слоев оболочки, т.е. когда .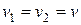

В этом случае легко получить значения 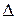, определяющее положение координатной поверхности оболочки, для которого жесткости 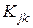превращаются в нули, т.е.

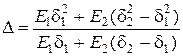(2.68)

Таким образом, приходим к заключению, что в общем случае многослойной оболочки при отсутствии ограничения (2.63) не существует такого расположения координатной ее поверхности, когда и для многослойной оболочки получаются соотношения упругости типа (2.47) при 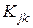=0.