Глава 2. Примарные и бипримарные группы

Примарные группы и их простейшие свойства

Определение 2.1.1. Группа 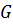называется примарной, если её порядок равен степени некоторого простого числа.

Теорема 2.1.1 (Свойства примарных групп). Пусть – примарная группа.

1. Центр неединичной примарной группы отличен от 1.

Доказательство. Пусть 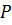‒ 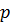-группа порядка 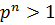и 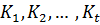‒ все различные классы сопряженных элементов группы 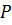, 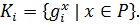Как известно, порядок класса сопряженных с 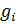элементов равен индексу централизатора 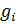, то есть 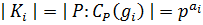. Каждый элемент центра составляет отдельный класс и наоборот, если 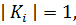то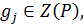

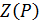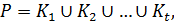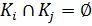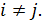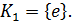где ‒ центр. Итак, где при Пусть Тогда 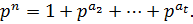Отсюда следует, что существует 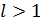такое, что 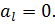Но тогда 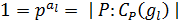и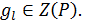

2. В примарной группе каждая собственная подгруппа отлична от своего нормализатора.

Доказательство. Пусть 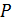‒ 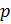-группа и 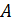‒ собственная подгруппа. Рассмотрим разложение группы 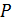в двойные смежные классы по :

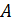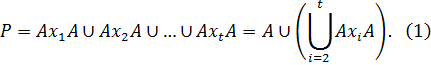
Здесь 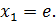Используя Теорему 1.2.2, получаем:

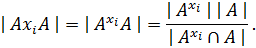
Теперь из разложения 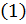имеем

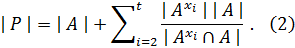
Пусть 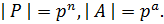Тогда из равенства 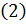следует, что

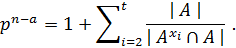
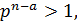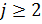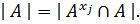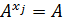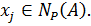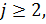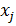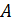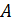Так как то в правой части равенства под знаком суммы имеются слагаемые, равные единице, то есть существует номер такой, что Это означает, что и Ввиду того что элемент не принадлежит и ‒ собственная подгруппа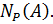

3. В примарной группе все максимальные подгруппы нормальны и имеют простые индексы.

Доказательство. Пусть 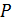‒ 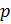-группа и 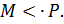По 2 пункту рассматриваемой леммы 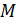‒ собственная подгруппа в своем нормализаторе 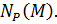Из максимальности 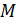следует, что 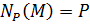и 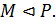По теореме о соответствии в фактор-группе 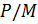нет нетривиальных подгрупп, поэтому согласно теореме Силова группа 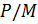имеет простой порядок.

4. В примарной группе пересечение неединичной нормальной подгруппы с центром группы отлично от единицы.

Доказательство. Пусть 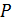‒ 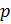-группа и 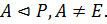Требуется доказать, что 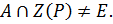Если 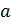‒ произвольный элемент из 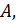то 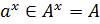для любого элемента 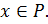Поэтому 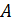состоит из классов сопряженных элементов группы 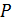, то есть 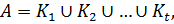где 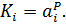Можно положить 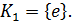Поскольку 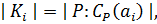то, считая 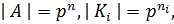получаем

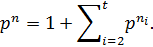
Теперь ясно, что существует 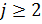такое, что 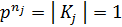и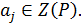

5. Минимальная нормальная подгруппа примарной группы имеет простой порядок и содержится в центре группы.

Доказательство. Пусть 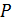‒ 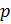-группа и 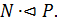Так как 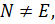то 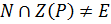, а поскольку 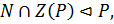то 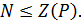Согласно теореме Силова в 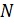существует элемент 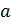простого порядка. Поэтому 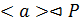и из условия 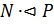следует, что 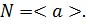Теорема доказана.

Определение 2.1.2. Пусть 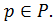Группа называется 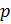-группой, если 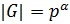, где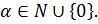

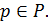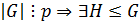Лемма 2.1.1 Пусть Если – абелева группа и , такая что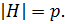

Теоремы Силова

Определение 2.2.1.

1) Пусть 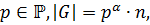где 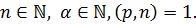Подгруппа 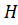группы 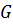называется силовской 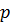-подгруппой группы 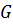( 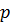-силовской, силовой), если 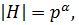и обозначается .

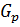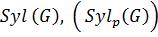
2) 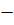множество всех силовских подгрупп группы 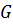(множество всех силовских 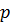-подгрупп группы ).

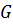Теорема 2.2.1 (Первая теорема Силова). Пусть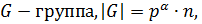

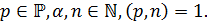Тогда в существуют силовские 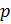-подгруппы.

Доказательство. Пусть – контрпример минимального порядка.

Расcмотрим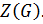

а) Пусть .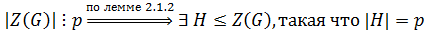

По лемме 1.2.2(2) 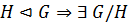. Так как .

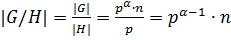Если 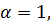то 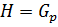. Пусть 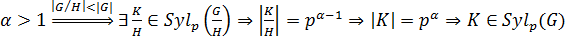. Противоречие.

б) Пусть 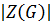не делится на 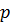. Рассмотрим формулу классов для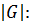

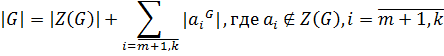
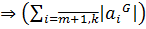не делится на 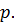Таким образом, 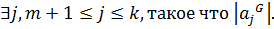Тогда по лемме 1.2.3(2) 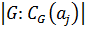не делится на 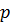. Следовательно, по теореме Лагранжа 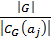не делится на 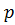. Соответственно 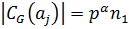где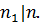

Допустим, что 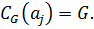Тогда 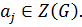Противоречие. Следовательно, 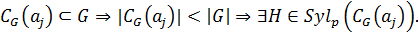Тогда .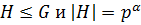

Таким образом, 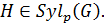Противоречие.

Из а) и б) вытекает, что контрпримера не существует. Следовательно, утверждение верно для любой 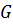. Теорема доказана.

Теорема 2.2.2 (Вторая теорема Силова).Всякая р-подгруппа группы содержится в некоторой силовской 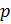-подгруппе группы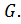

Доказательство. Пусть 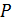‒ р-подгруппа группы . Тогда 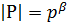, 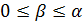. Если β=0 ⇒ .

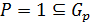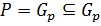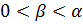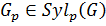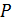Если α=β ⇒ . Пусть . Пусть . Рассмотрим разложение в двойные смежные классы по подгруппе и :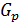

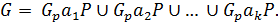
Следовательно, 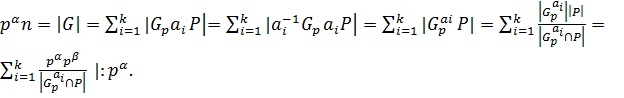Таким образом,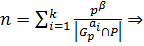 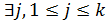такое что 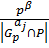не делится на 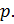Соответственно 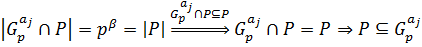, причем из 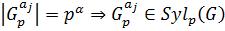. Теорема доказана.

Теорема 2.2.3 (Третья теорема Силова). Любые 2 силовские 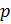-подгруппы группы 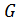сопряжены в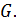

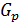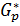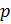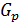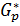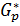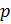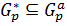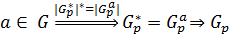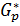Доказательство. Пусть и ‒ силовские -подгруппы группы . Покажем, что и сопряжены в . Так как ‒ -подгруппа группы , следовательно, по теореме 2.2.2 для некоторого и сопряжены в . Теорема доказана.

Теорема 2.2.4 (Четвертая теорема Силова).Число силовских р-подгрупп группы сравнимо с единицей по модулю 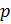и делит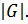

Доказательство. Пусть 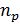‒ число силовских р-подгрупп группы . Пусть 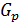‒ силовская р-подгруппа группы . Тогда, по теореме 2.2.3, множество всех силовских р-подгрупп имеет вид:

⇒ .

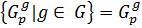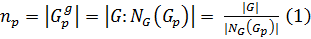Следовательно, 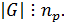Из (1) ⇒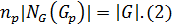

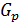Рассмотрим разложение в двойные смежные классы по подгруппе и :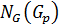

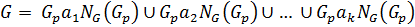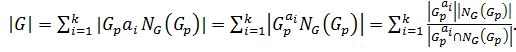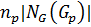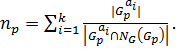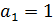. Соответственно, По формуле (2) ⇒ Пусть . Тогда 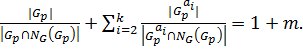Покажем, что 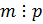. Допустим, что 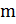не делится на 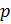. Тогда 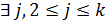, такое что

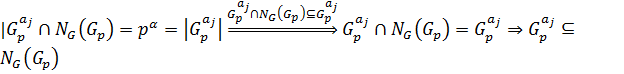. Таким образом, 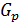и 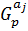‒ два разложения силовских р-подгрупп в 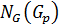. С другой стороны, 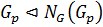. Следовательно, 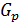‒ единственная силовская р-подгруппа в 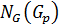, что является противоречием. Таким образом, 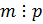⇒ ⇒ 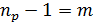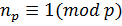. Теорема доказана.