Взаимосвязь определителя большего порядка и меньшего порядка. Разложение по строке.

Томский государственный университет систем управления и радиоэлектроники

Приходовский М.А.

Математика

Учебное пособие

(курс лекций)

Й семестр

Часть 1

для специальности:

09.03.03 «прикладная информатика в экономике»

(группы 446-1 и 446-2)

Томск

ТУСУР

Настоящее электронное учебное пособие составлено и скорректировано с учётом реального проведения лекций на ФСУ (профилирующая кафедра АСУ) в группах 446-1 и 446-2 осенью 2016 года.

Оглавление.

Часть 1 (сентябрь - октябрь)

Глава 1. МАТРИЦЫ.

§ 1. Действия над матрицами.

§ 2. Определители.

§ 3. Обратная матрица.

§ 4. Ранг матрицы.

§ 5. Элементы векторной алгебры.

Глава 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

§ 1. Введение, основные методы решения.

§ 2. Неоднородные системы с произвольной матрицей.

§ 3. Системы линейных однородных уравнений.

Глава 3. ЛИНЕЙНЫЕ ОПЕРАТОРЫ.

§ 1. Введение, основные понятия

§ 2. Собственные векторы

§ 3. Квадратичные формы.

Глава 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.

§ 1. Прямая на плоскости

§ 2. Плоскость в пространстве

§ 3. Прямая в пространстве

§ 4. Кривые и поверхности

Часть 1 (ноябрь - декабрь)

Глава 5. ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА.

§1. Множества и функции.

§2. Пределы.

§3. Бесконечно-малые и бесконечно-большие.

§4. Непрерывность.

Глава 6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ.

§1. Введение, основные методы.

2. Частные производные и градиент.

§3. Уравнение касательной, формула Тейлора.

§4. Экстремумы и строение графика.

§5. Основные теоремы дифф. исчисления

ЛЕКЦИЯ № 1. 02.09.2016

Глава 1. МАТРИЦЫ.

Действия над матрицами.

Определение матрицы. Матрицей размера называется прямоугольная таблица, состоящая из чисел (либо других объектов, например, функций), содержащая m строк и n столбцов.

Каждый элемент обозначается , где это номер строки, в которой он расположен, а - номер столбца.

! Обратите внимание: количество строк - это то же самое, что количество элементов в столбце, а количество столбцов равно количеству элементов в строке (заметим, что от каждого элемента 1-й строки начинается столбец, то есть сколько чисел в строке, столько и столбцов).

Если , то есть матрица А имеет размер 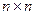то она называется квадратной матрицей порядка n.

Примеры матриц из жизни:

1. Таблица результатов ЕГЭ по нескольким предметам в группе учеников.

2. Таблица расстояний между каждой парой из n городов.

Кратчайшее расстояние между городами:

	Томск	Новосибирск	Кемерово
Томск
Новосибирск
Кемерово

По главной диагонали 0 , потому что до этого же города расстояние равно 0.

3. Расписание занятий. День недели и номер пары, каждый элемент - номер аудитории в этот день в это время.

4. Шахматная доска, 64 элемента, квадратная матрица порядка 8.

Сложение и вычитание матриц размера .

Эти операции определяются поэлементно, то есть суммируется или вычитается каждая соответствующая пара элементов и .

Примеры:

+ = ; =

Умножение матрицы на константу определяется следующим образом. В матрице все элементы умножены на коэффициент , то есть равны .

Умножение двух матриц.

* Нужно вспомнить из школьного курса операцию скалярного произведения двух векторов.

Если есть 2 матрицы, одна размера , другая , то их размеры называются согласованными. Такие матрицы можно умножать друг на друга.

Операция умножения матриц определяется следующим образом. Мысленно разобьём первую матрицу на строки, вторую - на столбцы. Для каждой строки 1-й матрицы и каждого столлбца 2-й матрицы определено скалярное произведение. Всего существует всевозможных скалярных произведений строк (1-й матрицы) на столбцы (2-й матрицы). Именно из них и состоит произведение, это матрица размера

Пример: = .

Для матриц размеров и существуют оба произведения, и . Но произведение в примере выше оказалось бы не матрицей 2 порядка, а 3 порядка, то есть из 9 элементов.

Умножение квадратных матриц.

В этом случае размеры всегда согласованы, и произведение - это тоже матрица .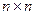

2 примера: = , =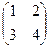

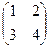обратите внимание, что даже для квадратных матриц далеко не всегда выполняется закон коммутативности, здесь .

* Существует такая матрица, которая во множестве матриц обладает свойством, аналогичным 1 во множестве чисел, то есть . Но как мы видели только что, матрица из всех единиц этим свойством не обладает, а вот если единицы только по главной диагонали, а вокруг - нули, то такое свойство будет выполняться.

Единичная матрица Е. Строение: , при .

2-го порядка: 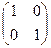, 3 порядка:

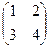
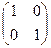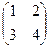= и = .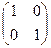

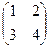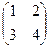(Аналог среди матриц первого порядка: число 1).

Свойства действий над матрицами:

коммутативность сложения

ассоциативность сложения

и дистрибутивность

ассоциативность умножения

и

.

О взаимосвязи матрицы с системой векторов.

Если в плоскости 2 вектора, т.е. каждый имеет по 2 координаты, можно построить матрицу 2 порядка. Аналогично, если дано 3 вектора в пространстве - можно построить матрицу 3 порядка.

Матрица, соответствующая этой векторной системе .

Определители.

Пусть дана матрица 2 порядка. .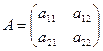

Определителем квадратной матрицы порядка 2 называется такое число:

(произведение элементов главной диагонали, минус произведение элементов побочной диагонали).

Геометрический смысл: модуль определителя равен площади параллелограмма, сторонами которого являются 2 вектора, координаты которых расположены по строкам (либо столбцам) матрицы.

Если бы мы просто вычисляли площадь параллелограмма, построенного на векторах (2,1) и (1,2), где ни один вектор не расположен вдоль координатной оси, то понадобилось бы найти длину основания, затем высоту. А с помощью определителя, S вычисляется гораздо короче.

Примеры. .

поменяем местами строки, изменится знак:

.

Заметим, что при введении определителя, умножаемые элементы всегда расположены так, что 2 из них не находятся в одной строке или в одном столбце. Кстати, кроме главной и побочной диагонали, в матрице порядка 2 таких наборов элементов больше нет.

Вообще, если расположить первые n натуральных чисел 1,2,3,..., n в некотором порядке, то есть не по возрастанию, а перепутать каким-то образом, то они образуют так наз. «перестановку».

Лемма. Существует n! перестановок порядка n.

Для n = 2 очевидно, перестановки только (12) и (21).

При n = 3. (123) (132) (213) (231) (312) (321)

На первом месте одно из 3 чисел, при этом оставшиеся 2 можно расставить на два места именно 2 способами. Получается 3*2 = 6 способов. (Заметим, что 6 = 3! )

Дальше, доказательство по индукции. Пусть теперь для (n-1) этот факт доказан. Рассмотрим для n. На первом месте может стоять любое из n чисел, и при каждой из этих ситуаций, остаётся (n-1) число, которые должны занять (n-1) место, а это возможно (n-1)! способами. Итак, получается что как раз равно n!, что и требовалось доказать.

Каждый набор элементов, которые мы перемножаем в определителе 2 порядка, можно задать с помощью перестановки: главная диагональ (12) побочная диагональ (21). Число i на месте j показывает, что когда мы находимся в строке номер j то надо выбрать элемент, находящийся в столбце номер i.

Большой прямоугольник в 1 строке, выбираем из 1 столбца, а когда он спустился во 2 строку, там из 2 столбца. Как на схеме:

таким путём мы как раз и получаем главную диагональ с помощью перестановки (12).

Определитель 3 порядка, примеры, методы вычисления.

= .

Запомнить легче всего так: с помощью произведений по 3 параллельным линиям.

Надо дописать копии 1 и 2 столбца справа, и соединить по 3 параллельных линии: главная диагональ и параллельные ей (показаны зелёным цветом), затем побочная диагональ и параллельные ей (показаны красным). Умножить тройки чисел по 3 зелёным линиям, и взять их со знаком «+» а по красным прибавить со знаком «—». (Кстати, вместо столбцов справа можно дописать две строки снизу, и получится то же самое).

Можно запомнить и с помощью треугольников, например, соответствует

Это один из двух треугольников, для которого главная диагональ - это средняя линия. Второй такой треугльник это .

В записи определителя 3 порядка =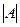

каждому элементу можно поставить в соответствие перестановку из 3 чисел.

Представьте себе прямоугольник, который сначала в 1-й строке, а затем спускается ко 2-й и 3-й, внутри него вправо и влево может двигаться квадрат, указывающий на какой-то из элементов. Запишем, в каком № столбца взяли элемент, когда находились в 1-й строке, затем так же во 2-й и 3-й. Например, для получится (231):

для соответствует (123) и т.д. напишем под каждым элементом свою перестановку:

(123) (231) (312) (321) (132) (213)

Видим, что при этом учтены все возможные перестановки, количество которых 3! = 6.

Рассмотрим подробнее, как знак определяется по перестановкам. Назовём инверсией такую ситуацию, когда большее число в перестановке расположено раньше, чем меньшее. Обозначим дугой каждую инверсию:

Если инверсий нечётное количество (1 или 3), то знак « - », если чётное (0 или 2) то «+».

Фактически, умножаем на , где k - число инверсий. Знак каждого произведения зависит от чётности или нечётности перестановки.

Причём, все рассмотренные наборы элементов, которые перемножаются между собой, обладают тем свойством, что никакие 2 из 3 не находятся в одной и той же строке либо одном и том же столбце. Таких наборов всего 6, и они все учтены. А для матрицы порядка 2 таких наборов всего 2, поэтому там определитель состоит всего из 2 слагаемых. Почему же они не могут быть в одной строке или столбце? Ответ простой: ведь перестановка состоит из разных чисел, то есть там нет одинаковых на двух местах, поэтому из одного и того же столбца 2 раза мы не выберем. Из одной строки тем более: находясь в некоторой строке, мы выбираем элемент только 1 раз.

А для матрицы 4 порядка потребуется найти все четвёрки элементов, так чтобы никакие два не оказывались в одной строке или одном столбце. Их будет 24 = 1*2*3*4 = 4!

Пример. = 1*2*4 + 1*3*0 + 2*0*1 — 0*2*2 — 1*3*1 — 4*0*1 = 8 — 3 = 5.

Пример. = 1*3*6 + 4*0*2 + 8*7*3 — 8*3*2 — 1*0*3 — 6*4*7 = 18 + 0 + 168 — 48 — 0 — 168 = -30.

ЛЕКЦИЯ № 2. 09.09.2016

Взаимосвязь определителя большего порядка и меньшего порядка. Разложение по строке.

Запишем разложение определителя порядка 3.

= .

Вынесем за скобку элементы первой строки (они есть в 2 из 6 слагаемых): .

То, что получилось в скобках, называют алгебраическими дополнениями элементов соответственно .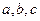

Выражение в 1-й скобке называется алгебраическим дополнением к элементу 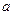, соответственно

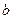- алгебраическим дополнением к , - алгебраическим дополнением к .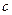

Заметим, что , , .

Если для элемента 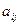и вычеркнуть всю строку и весь столбец, где он находится, образуется подматрица порядка (n-1). Определитель подматрицы порядка (n-1), которая получилась путём вычёркивания строки номер i и столбца номер j, называется дополняющим минором к элементу 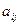. Всего таких миноров 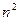, например для матрицы 3 порядка их будет 9 штук. Минор, соответствующий элементу 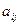, обозначается .

Мы видим, что в одних случаях алгебраическое дополнение равно минору, а где-то противоположно ему по знаку. Взаимосвязь алгебраических дополнений и миноров для произвольных i,j:

, то есть знаки меняются в шахматном порядке, для верхнего левого элемента 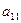знак «+».

Итак, определители можно вычислять разложением по строке:

= .

Общая запись в произвольных обозначениях: .

Разложение возможно по любой строке или по любому столбцу. Так, например, в той же рассмотренной ранее записи можно собрать пары слагаемых, содержащих и точно так же вынести за скобку, получится = =

= здесь чередование знака начинается с минуса, что и должно быть в соответствии с шахматным порядком, о чём сказано выше.

Заметим, что если матрица треугольная, то для вычисления 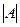можно просто умножить все числа по диагонали.

.

Это объясняется очень просто: если разложить по строке, где есть всего один ненулевой элемент и (n-1) нулей, то сразу переходим к минору меньшего порядка, для него получается аналогичное действие, и так до конца. Рассмотрим на примере:

= = = = 6.

Для диагональных матриц, как и для треугольных, верен такой же факт.

Рассмотрим ещё пример с определителем треугольной матрицы 4 порядка:

= = = 12.

Поэтому приведение к треугольному виду очень часто используется для вычисления определителей. Метод Гаусса, который будет подробно изучен в теме «системы уравнений», в полной мере может применяться и для вычисления определителей. Если обнулить элементы ниже главной диагонали, то вычисление определителя сильно упростится.