Свойства операции умножения вектора на число

1.l( + ) = l + l; 3.(l + m) = l + m;

2.l(m ) = (lm); 4.1· = .

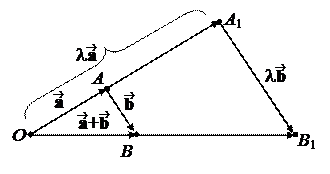Доказательство. 1.Пусть

= , = ,

l= , l = .

Тогда по правилу треугольника

+ = , l + l = .

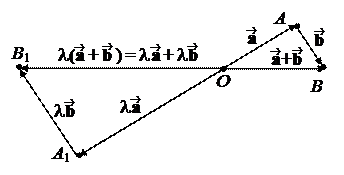Нам требуется доказать, что l( + ) = .

Из (**) вытекает по-добие треугольников ΔOAB ~ ~ ΔOA₁B₁ по двум сторонам и углу между ними. Поэтому | | и ||= l||.

Отсюда, с учетом + = , вытекает l( + ) = . На первом рисунке изображен случай l > 0, а на втором – l < 0. В случае же l = 0, обе части равенства дают .

Упражнение. Остальные свойства докажите самостоятельно.

Теорема 1(первый признак коллинеарности векторов). Для того, чтобы ненулевые векторы и были коллинеарны, необходимо и достаточно, чтобы существовало такое число l , что = l.

Доказательство. Достаточность вытекает непосредственно из определения произведения вектора на число. Если = l, то по определению ||.

Необходимость. Пусть ||.

1 случай: ­­ . Положим l =½½ /½½ > 0. Тогда

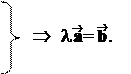l ­­ Þ l ­­ ,

½l½ =½l½½½ = l| |= | |=½½.

2 случай: ­¯ . Положим l = –½½ /½½ < 0. Тогда

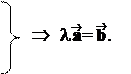l ­¯ Þ l ­­ ,

½l½ =½l½½½= –l| |= | |=½½.

Что и требовалось доказать.

В процессе доказательства мы показали, как решить следующую задачу: найти вектор сонаправленный с данным вектором и имеющий заданную длину ½½= b. Это будет вектор = . В частности, единичный вектор ­­ находится так: = . Такой вектор называется ортом вектора .

Угол между векторами. Ориентация пары векторов на плоскости или тройки векторов в пространстве.

Определение. Пусть и – два ненулевых вектора. Отложим их из одной точки О: = , = . Тогда углом между векторами и называется угол между лучами OA и OB, т.е. a =ÐAOB. Пишем a =Ð( , ).

Если речь идет о векторах на плоскости, то можем ввести понятие ориентированного угла между векторами. Если кратчайший поворот

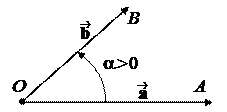от луча OA к лучу OB осуществляется против часовой стрелки, то считаем, что a > 0, а если по часовой – то a < 0 . Таким образом, – p < a £ p . Если a > 0, то пара векторов (, ) называется правой, а если a < 0 – то левой.

В пространстве понятие ориентированного угла не имеет смысла. Если посмотреть на плоскость, в которой лежат лучи OA и OB с одной стороны, то увидим, что кратчайший поворот от OA к OB осуществляется в одном направлении, а если посмотреть на плоскость с другой стороны, то мы увидим тот же поворот в другом направлении.

Пусть в пространстве даны три некомпланарных вектора , , . Отложим их из одной точки О: = , = , = . Тройка векторов (, , ) называется правой, если кратчайший поворот от луча OA к лучу OB, если смотреть из точки C , выглядит как осуществляющийся против часовой стрелки. Соответственно, если этот поворот выглядит как осуществляющийся по часовой стрелке, то тройка векторов (, , ) называется левой. На рисунке изображена правая тройка векторов.

Проекция вектора на ось.

Пусть l – некоторая прямая в пространстве. Выберем точку OÎ l и единичный вектор ||l.Построим направленный отрезок = . Прямая l с отрезком называется осью. Иногда говорят, что ось – это прямая, на которой задано направление.

Определение. Пусть – произвольный вектор, а – произвольный направленный отрезок, который представляет . Опустим перпендикуляры AA₁ и BB₁ на прямую l. Пусть = . Тогда вектор

называется векторной проекцией вектора на ось l и обозначается p_l.

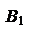
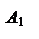
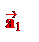
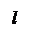
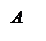
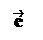
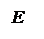
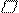
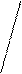
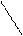
Мы имеем ||. Поэтому согласно теореме 1 существует такое число p, что = p. Это число называется скалярной проекцией вектора на ось l . Поскольку –

единичный вектор, то p – это длина вектора , если ­­, и p = – ||, если ­¯. Будем обозначать скалярную проекцию так: P_l.

Зная скалярную проекцию вектора мы можем найти его векторную проекцию:

p_l = (P_l ); (*)

Если ^, то, очевидно, A₁= B₁ и P_l = 0.

Необходимо еще доказать, что определения скалярной и векторной проекции корректны, т.е. не зависят от выбора направленного отрезка , который представляет вектор . Другими словами, если мы отложим вектор от другой точки, то его скалярная и векторная проекции не изменятся,– и это надо доказать.

Проведем через точки A и B плоскости a и b перпендикулярно l. Тогда ½p½=½P_l½ есть расстояние между a и b .Выберем другой направленный отрезок , представляющий и проведем через точки A¢, B ¢ плоскости a¢ и b¢ перпендикулярно l. Направленные отрезки и эквивалентны, а значит, они совмещаются параллельным переносом. При этом переносе плоскость a совместится с a¢, а плоскость b – с b¢. Значит, расстояние между a¢ и b¢ равно расстоянию между a и b, и оно равно ½p½. Поэтому ½p½ не зависит от выбора направленного отрезка. Направление векторной проекции также не изменится при переносе, поэтому и знак p не изменится. Итак, скалярная проекция не зависит от выбора направленного отрезка, представляющего . В силу равенства (*) p_l также не зависит от выбора направленного отрезка.

Теорема 2. Свойства проекции вектора на ось.

1.P_l =| |cosÐ(, );

2.P_l(l ) = lP_l , p_l(l ) = l(p_l );

3.P_l( + ) = P_l + P_l, p_l( + ) = p_l + p_l .

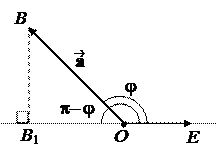Доказательство. 1. Поскольку определение проекции не зависит от выбора точки A ,из которой отложен вектор , мы можем отложить его из точки О. Обозначим j =Ð(, ).

1 случай: j £ p/2. Тогда из DOBB₁ получим, что

p =½OB₁½=½OB½· cos j = | |cos j.

2 случай: j > p/2. Тогда из DOBB₁ получим, что

p = –½OB₁½= –½OB½· cos (p– j) = | |cos j.

2. Для скалярных проекций:

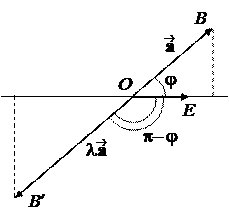1 случай: l > 0. Тогда l ­­ и Ð(, l ) = j. Значит,

P_l(l ) =½l½cos Ð(,l ) =

= l| |cos j = lP_l .

2 случай: l < 0. Тогда l ­¯ ,

Ð(, l ) = p – j и cosÐ(,l ) = – cos j,

P_l(l ) =½l½cosÐ(,l ) = –l| |(– cos j) =

= l| |cosÐ(, ) = lP_l .

3 случай: l = 0. Тогда равенство очевидно.

Для векторных проекций с помощью равенства (*) получаем:

p_l(l ) = (P_l(l )) · = l(P_l ) · = l(p_l ).

3.Доказательство для векторных проекций показано на чертеже, но только для случая векторов на плоскости. Рисунок для векторов в пространстве можно найти в учебнике [10].

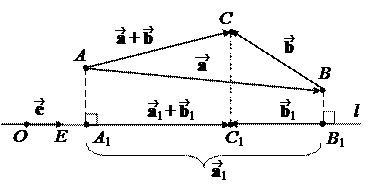Для скалярных проекций равенство вытекает из равенства для векторных проекций. Например, в случае, изображенном на втором рисунке,

P_l( + ) = |A₁C₁|,

P_l = |A₁B₁|,

P_l = – |B₁C₁|,

и мы видим, что

|A₁C₁|= |A₁B₁|+(– |B₁C₁|).