Умножение матрицы на число и сложение матриц

МАТРИЦЫ

Оглавление.

1. Определение матриц.

2. Квадратные матрицы.

3. Действия с матрицами

4. Ранг матрицы.

5. Обратная матрица.

Системы линейных уравнений.

А. Метод Гаусса.

6.б. Формулы Крамера.

6.в. Матричный метод.

Системы линейных уравнений общего вида.

Определение матриц

Прямоугольная таблица, содержащая 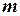строк и 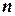столбцов, называется матрицей размера .

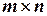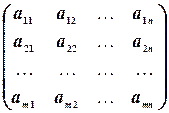
Числа 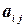называются элементами матрицы. Каждый элемент матрицы снабжен двумя индексами: первый индекс указывает номер строки, второй — номер столбца, в котором расположен этот элемент.

Матрицы обозначают буквами , , 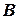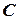и т. д. Например,

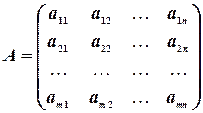
или сокращенно в виде .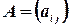

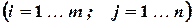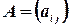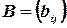Две матрицы и считаются равными, если равно число их строк и число столбцов и если равны элементы, стоящие на соответствующих местах этих матриц равны, то есть 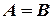, если .

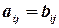Часто приходится рассматривать матрицу, столбцами которой являются строки матрицы . Эта матрица называется транспонированной к и обозначается через .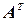

Пусть дана матрица . Переставим строки со столбцами. Получим матрицу

_,

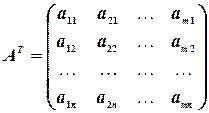которая будет транспонированной по отношению к матрице .

Квадратные матрицы

Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число ее строк, равное числу столбцов, — порядком квадратной матрицы.

Множество всех элементов квадратной матрицы, которые лежат на отрезке, соединяющем ее левый верхний угол с правым нижним, т. е. совокупность элементов 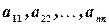называется главной диагональю, а множество всех элементов, которые лежат на отрезке, соединяющем ее правый верхний угол с левым нижним, - побочной диагональю.

Квадратная матрица называется треугольной, если ее элементы, которые находятся над главной диагональю или под главной диагональю, равны нулю, т. е. матрицы вида

,

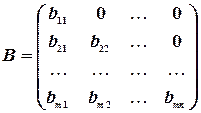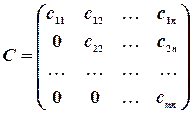
являются треугольными. Матрица 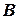называется треугольной снизу, а матрица — треугольной сверху.

Квадратная матрица называется диагональной, если ее элементы, которые находятся вне ее главной диагонали, равны .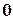

.

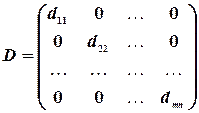Действия с матрицами

Умножение матрицы на число и сложение матриц

По определению, чтобы умножить матрицу на число 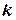, нужно каждый элемент матрицы умножить на это число.

Пример 1. Умножить матрицу на число

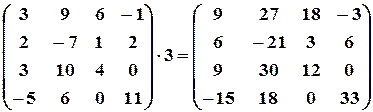
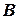Складывать можно только матрицы с одинаковым числом строк и столбцов. Суммой матриц и называется матрица 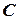, элементы которой равны суммам соответствующих элементов матриц и : .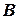

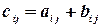Пример 2. Сумма двух матриц

.

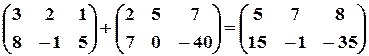Матрица, все элементы которой равны нулю, называется нулевой и обозначается через 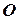. Для любой матрицы имеем , .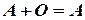

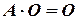Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

1) ,

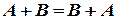2) ,

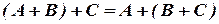3) ,

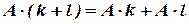4) ,

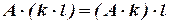5) .

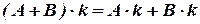где , , 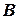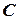- матрицы, 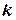, 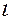- числа.

Произведение матриц

Произведение матрицы на матрицу 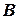определено только в том случае, когда число столбцов матрицы равно числу строк матрицы 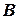. В результате умножения получим матрицу 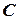, у которой столько же строк, как у матрицы , и столько же столбцов, как у матрицы .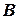

По определению элемент 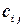матрицы 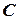равен сумме парных произведений элементов 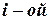строки матрицы , на соответствующие элементы 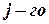столбца матрицы .

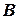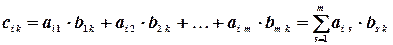
Пример 3. Найти произведение матриц

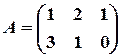и .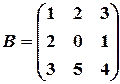

Решение. Имеем: матрица размера 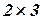, матрица 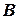размера 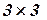, тогда произведение 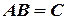существует и элементы матриц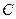ы равны

, , ,

, .

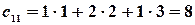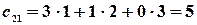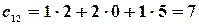
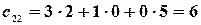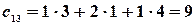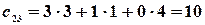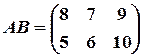, а произведение 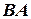не существует.

Пример 4. Найти произведение матриц

,

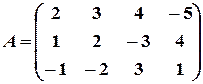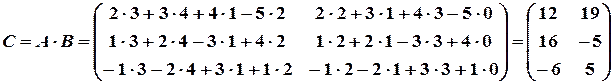
Очевидно, что произведение матриц не обладает перестановочным свойством, т.е. некоммутативно. Если все-таки выполняется равенство 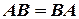, то матрицы и 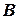называются перестановочными.

Свойства произведения матриц:

1) 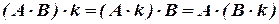, где 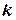-число;

2) ;

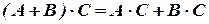3) ;

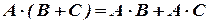4) .

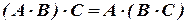Единичной матрицей называется диагональная матрица, у которой все элементы равны 1.

.

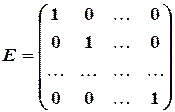Свойство единичной матрицы: 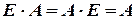для любой квадратной матрицы .

Рассмотрим произвольную квадратную матрицу , порядка 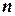. Если существует такая матрица 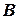, что 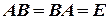, то говорят, что обратима, а 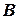называют обратной матрицей для матрицы .

Определитель матрицы

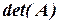Определителем квадратной матрицы называется число, которое обозначается как или 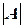и вычисляется при помощи следующих трех правил.

Правило 1. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали.

Замечание: Определитель одноэлементной матрицы равен самому элементу.

Правило 2. Общий множитель элементов любой строки или столбца матрицы можно вынести за знак определителя.

Замечание: Определитель матрицы, у которой строка или столбец состоит только из нулей, равен .

Правило 3. Определитель матрицы не изменится, если к одной из строк (столбцов) матрицы прибавить другую строку (столбец) этой матрицы.