Краткая теория

Молярной теплоёмкостью вещества называется физическая величина С, численно равная количеству тепла, которое нужно сообщить одному молю вещества для повышения его температуры на 1К в некотором термодинамическом процессе.

Молярная теплоёмкость

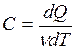(ν – число молей газа).

Для данного вещества величина С зависит от условий, при которых происходит передача тепла. Так, для газов молярная теплоёмкость C_p при изобарном процессе (p = const) отличается от молярной теплоёмкости C_v при изохорном процессе (V=const). Действительно, по первому началу термодинамики (dQ = dU + dA) для элементарного изохорного процесса dQ = dU , где U – внутренняя энергия одного моля газа и тогда 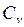= 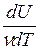(dU = νC_vdT). В то же время для элементарного изобарного процесса

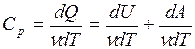
(dA =pdV - элементарная работа, совершенная газом при расширении).

В результате C_P= C_V+ 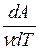, т.е. C_p>C_v. Физический смысл этого можно пояснить следующим примером. Пусть газ заключен в цилиндр с подвижным поршнем. Если поршень закреплен, то для повышения температуры газа на dTему нужно сообщить количество тепла dQ = νС_vdT. Если же поршень свободен, то газ при нагревании расширяется, передвигая поршень, и совершает тем самым работу против внешних сил. Для этого требуется дополнительное количество тепла, так что dQ_p> dQ_v и C_p>C_v.

Так как dU =ν 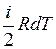, а с другой стороны, dU=νC_vdT, то 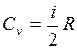(i – число степеней свободы молекулы данного газа). Согласно уравнению Майера C_p = C_v + R. Тогда .

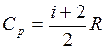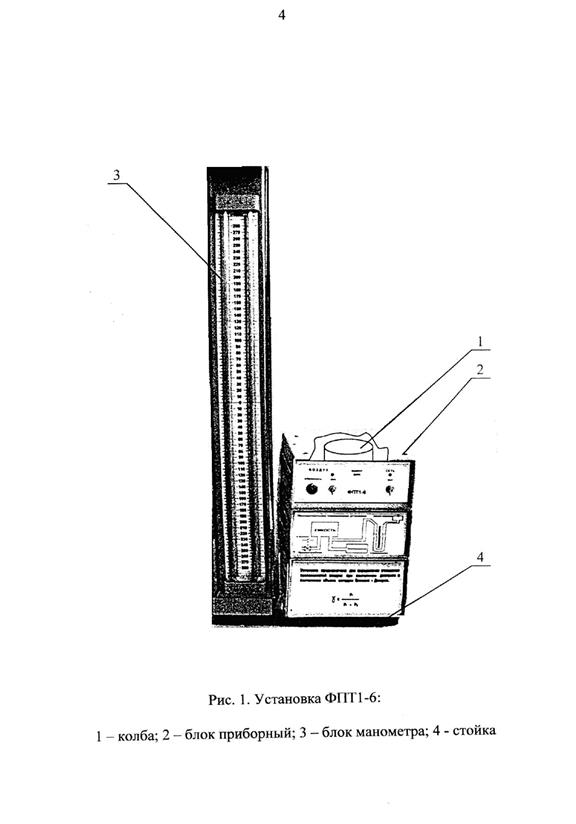
2→3 воздуха, оставшегося в колбе). Когда температура воздуха Т₃ в сосуде сравняется с первоначальной Т₁ (температурой окружающего воздуха), то давление воздуха в колбе станет равным p₃. При адиабатическом расширении воздуха 1→2, согласно уравнению Пуассона:

p₁V₁^γ = p₂V₂^γ, (1)

где V₁ – первоначальный объем воздуха, который при расширении займет объем V_к колбы. С другой стороны,

p₁V₁ = p₃V₃. (2)

так как в соотношении 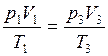температура T₁ равна температуре T₃..

Поскольку V₂=V₃=V_к , то из (1) и (2) получаем:

.

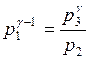Отсюда (γ – 1)lgp₁ = γlgp₃- lgp₂ и тогда: .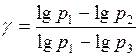

Так как в условиях опыта давления p₁ и p₃ мало отличаются от p₂ (p_а), то с достаточной точностью можно записать

.

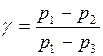Так как второе колено манометра открыто, то p₁ = p_м1 + p₂ , p₃ = p_м2 + p₂ , где p_м1 и p_м2 – показания манометра ( в кПа) для установившихся состояний 1 и 3 соответственно. Тогда

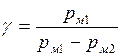. (3)