Модели ИС с дискретным временем
Многие ИС действуют циклически, ввиду чего результат измерения имеет вид:
y(t)=y(ti)[1(t-jT)-1(t-(j+1)T)]=y(ti)Hj, (3.32)
где j = 0, 1, 2, ...; tj = jT.
Символом Hj обозначена функция
Hj=1(t-jT)-1[t-(j+1)T)], (3.33)
которая описывает действие выходной ступени преобразования цифровых ИС, называемой регистром. Регистр — это устройство памяти, в котором фиксируются результаты измерения за время одного цикла измерения. Регистр управляется блоком управления ИС.
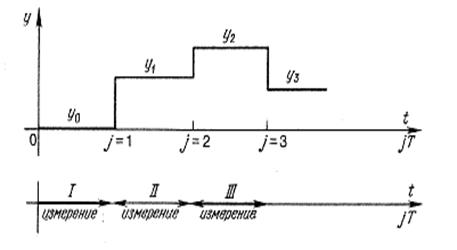
Рис. 3.10. Выдача результата измерения цифровой ИС
Во время первого измерения ИС показывает результат у0, т. е. состояние перед измерением, во время второго измерения — результат первого измерения у1,и т. д. Это иллюстрирует рис. 3.10. Индекс j обозначает номер измерения, а Т — период (время) измерения. Время измерения поделено на элементарные временные шаги iΔt, идентифицированные порядковым номером i. Измерения начинаются с момента i = 0. В моменты времени iΔt может произойти: а) изменение состояния элементов ИС либо величин, описывающих это состояние; б) изменение структуры ИС.
Состояние элемента описывается величиной ui или величинами uki (k = 1, 2, 3, ...) в моменты и (iΔt), а поддержание этого состояния в течение временного шага — функцией Hi (3.44), как это представлено в формуле (3.43). Примеры моделирования ИС с дискретным временем показаны ниже.
Цифровой вольтметр с двойным интегрированием. Структурная схема цифрового вольтметра представлена на рис. 3.11. Картину прохождения сигналов по отдельным ступеням преобразования дает рис. 3.12. В первом периоде работы устройства осуществляется интегрирование напряжения Ux, и выходное напряжение интегратора имеет вид
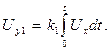 (3.34)
(3.34)
С момента i = 0 счетчик L отсчитывает импульсы, вырабатываемые генератором импульсов:
Uг,м,=d(t-iDt), i = ... -2, -1, 0, 1, 2, 3, …, (3.35)
а состояние счетчика в текущий момент описывается уравнением
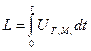 = Uг,нt < N0 , (3.36)
= Uг,нt < N0 , (3.36)
где
NDt<t<(N+1)Dt. (3.37)
Если к моменту времени t1счетчик достигнет состояния переполнения N0, то интегрирование напряжения Ux прекращается и происходит переключение на входе интегратора напряжения U0. Первый период измерения заканчивается, когда
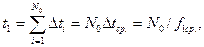 (3.38)
(3.38)
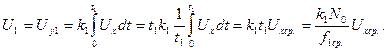 (3.39)
(3.39)
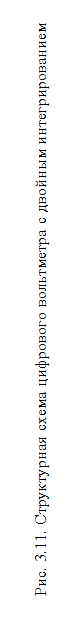
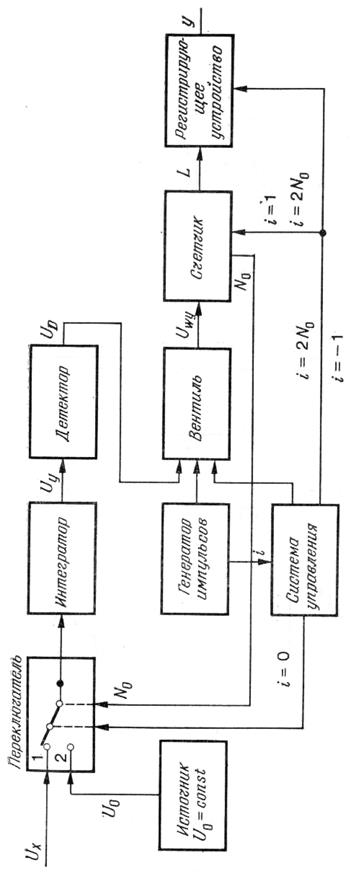
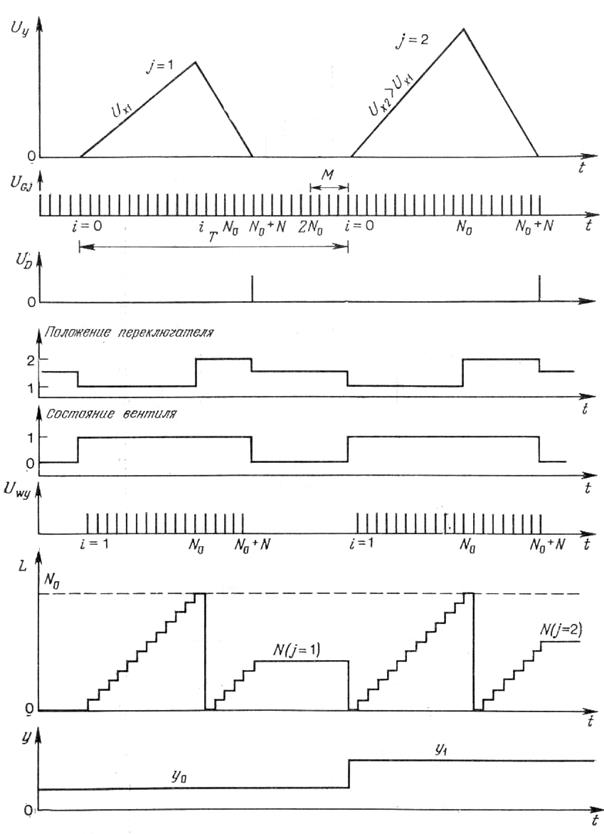
Рис. 3.12.Характеристики сигналов в цифровом вольтметре с двойным интегрированием
Во втором периоде измерения j=l выходное напряжение интегратора уменьшается в соответствии с уравнением
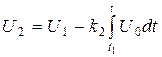 (3.40)
(3.40)
и в момент t2 достигает нуля. Тогда детектор генерирует импульс
UД=d(Uy)=d(t-t2) (3.41)
на закрытие вентиля (ключа), и последующие импульсы от генератора до счетчика не доходят.
Найдем t2. В момент, когда интегрирование заканчивается, выходное напряжение генератора достигает порога срабатывания детектора UД:
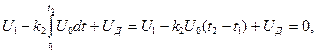 (3.42)
(3.42)
откуда с учетом (3.39) получается:
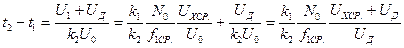 . (3.43)
. (3.43)
Здесь UДx — величина нечувствительности детектора в состоянии равновесия.
В момент t2 состояние счетчика достигает
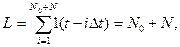 (3.44)
(3.44)
при этом N соответствует условию (3.37) для момента закрытия ключа,
(N0+N)Dt<t2<(N0+N+1)Dt . (3.45)
Измерение времени t2 выполняется путем считывания временных шагов Dti, так что
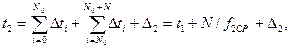 (3.46)
(3.46)
где
0<D2£DtN+1 , (3.47а)
или
0<D2 f2N£ 1. (3.47б)
Отсюда после подстановки (3.43) в выражение (3.46) получаем
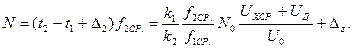 (3.48)
(3.48)
Это – уравнение преобразования интегрирующего вольтметра, где измеряемой величиной является среднее значение напряжения x=Uxср., а выходной величиной – y=N. Величина Δz = Δ2f2CP – погрешность считывания, значение которой случайно на временном интервале.
Представленная модель учитывает некоторые реальные свойства цифрового вольтметра – неодинаковые постоянные интегрирования и частоту генератора импульсов в первом и втором циклах измерения, а также нечувствительность детектора UД. Процедура калибровки определяется идеальной моделью, т. е. равенством (3.48) при k1=k2 , f1ср.=f2ср., UД=0, т. е. в идеальном случае:
(N/N0)U0<U*x ср.<[(N+1)/N0]U0. (3.49)
После подстановки в эту процедуру действительной модели (3.48) получаем
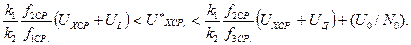 (3.50)
(3.50)
Время измерения составляет T=2N0Dt+MDt, причем за Μ временных шагов осуществляются перенос состояния счетчика в регистр, обнуление счетчика и интегратора.
Уравнения преобразования (3.34), (3.36), (3.37), (3.39) позволяют определить состояние цифрового вольтметра в каждый момент времени t, так что представленная модель является динамической.
3.3. Моделирование источников погрешностей.
Вероятностные модели
При моделировании погрешностей стараются учитывать реальные свойства конструктивных элементов ИС. Источниками погрешности могут быть:
1) явления, имеющие молекулярный характер,
2) влияние некоторых факторов окружающей среды на явления внутри ИС,
3) процессы старения и износа (изменения свойств элементов, из которых построена ИС, носят случайный характер).
В моделировании характеристик явлений такого рода принимаются постоянными значения коэффициентов уравнения преобразования. Вот ряд примеров таких моделей.
Явления молекулярного характера
1. Количество частиц, излучаемых источником изотопов, на интервалах времени подчиняется распределению Пуассона. Скорость частиц неодинакова и приблизительно описывается распределением Максвелла. В детерминированных моделях оперируют средним потоком частиц 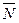 . На рис. 3.13 показано, как с увеличением времени усреднения (либо с повышением активности источников) ослабевает случайный характер явления.
. На рис. 3.13 показано, как с увеличением времени усреднения (либо с повышением активности источников) ослабевает случайный характер явления.
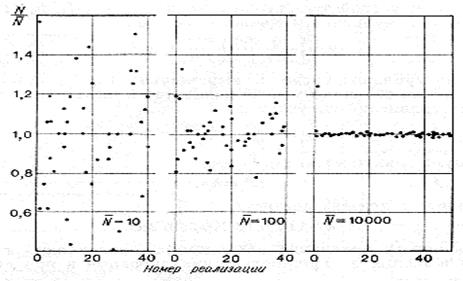
Рис. 3.13. Распределение значений числа N частиц для различных средних значений потока частиц 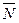
2. Удары частиц газа в нить торсионных весов либо гальванометра вызывают флуктуации подвижного органа с отклонением Δφ, причем среднеквадратическое отклонение составляет
Δφск= 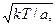 (3.51)
(3.51)
где
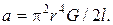
Здесь G — модуль поперечной упругости материала нити, r, I — размеры нити (радиус сечения и длина), k — постоянная Больцмана (универсальная газовая постоянная), Т — абсолютная температура.
3. Тепловые шумы в сопротивлениях описывает формула Найквиста:
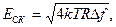 (3.52)
(3.52)
где EСК – среднеквадратическое значение электродвижущей силы для полосы частоты Df; R – величина сопротивления.
4. Флуктуационный (дробовой) шум, возникающий в фотоэлектронных умножителях (и в электронных лампах), будучи эффектом катодной эмиссии электронов, характеризуется током эмиссии
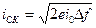 либо
либо 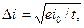 (3.53)
(3.53)
где i0 — среднее значение тока за период t; e — заряд электрона.
5. Токовый шум, обусловленный молекулярной природой электричества, проявляется в измерительных датчиках (контурах)смалой силой тока, таких как детекторы излучения, тонкопленочные резисторы, полупроводники и т. д. Среднеквадратическое значение этого шума определяется по эмпирической формуле
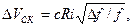 (3.54)
(3.54)
где с — постоянная, R — сопротивление, i —сила тока, f — частота.
В электронных системах проявляются:
1) токовые шумы с интенсивностью, обратно пропорциональной частоте,
2) тепловые и дробовые шумы, не зависящие от частоты,
3) паразитные шумы для очень высоких частот.
Молекулярный характер имеют явления теплообмена путем теплопроводности, излучения и конвекции, давления жидкости или газа и много других явлений.
Влияние окружающей среды
Влияние среды на ИС обусловлено зависимостью свойств конструктивных элементов от окружающих условий. Почти все свойства материалов зависят от температуры, ИС питается от энергетической сети и т. д. Выявленные и исследованные зависимости учитываются в математической модели путем формулирования зависимости выходных величин от воздействующих величин x1, …, xm-1 для различных значений х. Можно также учесть динамические состояния. Но все явления охватить моделью не удается.
Сохраняется:
1) остаточное влияние колебаний напряжения в сети,
2) влияние солнечной радиации (его можно уменьшить, но трудно полностью исключить),
3) изменения давления в помещении вследствие напора ветра, а также другие явления подобного характера.
Остаточное (неучтенное) влияние среды учитывается в моделях путем введения переменной z.
Старение и износ
Можно рассмотреть также вопросы старения и износа материала. Это явления, продолжительные по времени, протекающие обычно монотонно.
1. Так, например, старение изоляции подчиняется закону Аррениуса
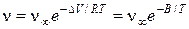 , (3.55)
, (3.55)
где 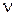 — скорость химических реакций, R — газовая постоянная, Т —температура, DV— энергия активации,
— скорость химических реакций, R — газовая постоянная, Т —температура, DV— энергия активации, 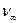 — постоянная реакции, В=const.
— постоянная реакции, В=const.
2. Скорость испарения материала из горячего волокна описывается выражением
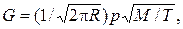 (3.56)
(3.56)
где 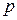 — давление, Μ — молекулярная масса материала, R — газовая постоянная, Т — температура.
— давление, Μ — молекулярная масса материала, R — газовая постоянная, Т — температура.
К эффектам старения также относятся:
3. Истирание и износ подвижных частей, ход и продолжительность которых можно оценить подобным же образом.
4. Загрязнения поверхности оптических элементов, токопроводящие, химически и физически активные, всегда являются помехами, хотя они и трудны для аналитического описания.
В ИС множество элементов различным образом подвержены старению и износу, и наблюдается итоговый эффект, который не всегда монотонен.
В моделировании источников погрешностей целью является детерминированная модель ИС. Входящие в модель коэффициенты b1, …,bi однозначно зависят от конструктивных параметров а1, …,ak[11]:
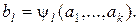 (3.57)
(3.57)
На каждый из конструктивных параметров могут влиять молекулярные явления либо старение материалов, ввиду чего данный параметр aj содержит постоянную aj0 и случайную 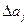 составляющие, а именно:
составляющие, а именно:
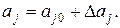 (3.58)
(3.58)
Для учета этих явлений приходится вводить специальные источники погрешностей, описывающие, например:
1) интенсивность тепловых шумов в резисторе,
2) сопротивление стыков в контуре, так как они не следуют непосредственно из детерминированной модели.
Каждый источник как случайная переменная характеризуется распределением вероятностей и спектральной плотностью. Если источник погрешности локализован в структурной схеме, а его характеристики и модель известны, то степень влияния этого источника на выходную величину можно рассчитать.
Сложность этой задачи обусловлена следующими причинами:
1. Кроме постоянных значений величин x1,…, xm, что позволяет принять статическую модель, внутри ИС существуют источники случайных величин, для синтеза которых следует использовать динамическую модель.
2. Внутренние источники погрешностей характеризуются весьма широким спектром частот; высокие частоты возникают в результате молекулярных явлений, очень низкие — в процессах старения. Распределения вероятностей внутренних источников погрешностей могут быть разнородными. Процессы старения ведут к тому, что общий эффект погрешностей может представлять собой нестационарный процесс.
3. Нелинейные элементы могут значительно расширять спектры шумов, а усредняющие элементы — зауживать их. Поэтому приблизительные оценки могут быть ошибочны.
Ниже мы рассмотрим способ моделирования источников погрешностей и некоторые свойства преобразования их.
Нелинейные элементы
Свойства модели. Рассматриваются безынерционные нелинейные элементы (без динамики). Источник погрешностей на входе элемента описывается распределением вероятностей р(х) и спектральной плотностью Sx(ω). Это означает, что случайная величина X стационарна. На выходе элемента с характеристикой y=f(x) получается стационарная случайная переменная Y.
1-й этап. Определение вероятностного распределения. Исходными данными для расчета являются конструктивные параметры a1, …, ak, а также многомерное распределение вероятностей p(a1, …, ak) и граничные распределения p1(a1, …, ak). Коэффициентами модели служат величины b1, …, bi, определяемые выражением (3.57) при i=1, 2, ..., l, а именно:
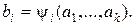
Функцию ψi можно посредством последовательных подстановок представить в виде элементарных функций: суммы, разности частного и произведения двух первичных переменных aj или функции одной переменной. Расчетные формулы для элементарных функций приведены в табл. 3.1.
2-й этап. Определение спектральной плотности. Исходные данные: спектральная плотность Sx(ω) либо функция корреляции Κx(τ) стационарного источника погрешностей, а также характеристика элемента[12]. Для линейного элемента существует связь
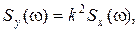 (3.59)
(3.59)
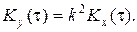 (3.60)
(3.60)
Относительно просто можно рассчитать (по определению) функцию корреляции на выходе элементов с квадратичной или многомерной характеристикой. Поэтому прочие характеристики следует аппроксимировать многомерной характеристикой.
Таблица 3.1.
Формулы для расчета распределения вероятности функции непрерывных случайных переменных
| Функции | Зависимые переменные | Независимые переменные |
Одномерная Z=f(X), если существуют X=w(X) и 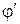 | 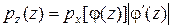 | |
| Z=X+Y | 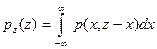 | 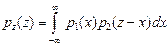 |
| Z=X-Y | 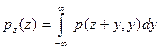 | 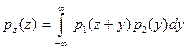 |
| Z=XY | 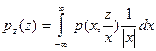 | 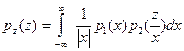 |
| Z=X/Y | 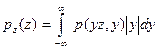 | 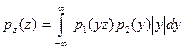 |
Нижеприведенные формулы относятся к случайной переменной X со средним значением, равным нулю (E[X] = 0), а также с нормальным распределением вероятностей. Если
Y=X2, (3.61)
то, обозначив
X1=X(t), X2=X(t+t), (3.62)
можно рассчитать функцию корреляции по определению
Ky(t)=E{[X12-E(X12)][X22-E(X22)]}. (3.63)
После выполнения преобразований и расчетов получаем
Ky(t)=2[Kx(t)]2 .(3.64)
Спектральная плотность вычисляется по формуле Винера — Хинчина
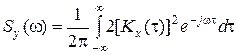 . (3.65)
. (3.65)
Свешников предлагает рассчитывать интеграл (3.65) по формуле
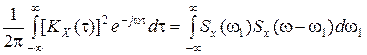 , (3.66)
, (3.66)
что значительно упрощает расчеты.
Если характеристика элемента имеет вид:
Y=b0+b1X+b2X 2, (3.67)
где X – случайная переменная с нормальным распределением и средним значением, равным нулю, то
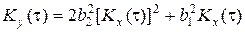 , (3.68)
, (3.68)
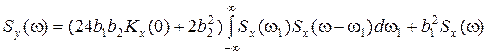 . (3.69)
. (3.69)
Для нелинейного элемента с характеристикой
Y=XU, (3.70)
если E(X)=E(U)=0, обе переменные X, U имеют нормальные распределения, а характеристики их известны, то
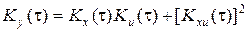 , (3.71)
, (3.71)
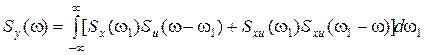 . (3.72)
. (3.72)
Примеры (3.67), (3.70) позволяют шаг за шагом рассчитать очень сложные характеристики элементов. Однако расчеты усложняются, так как по достижении нелинейности распределение выходной величины перестает быть нормальным.
