Каноническое уравнение прямой
Тема 10. Уравнение прямой на плоскости
Общее уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением первой степени вида 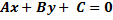
где A, B и С – числовые коэффициенты, одновременно не равные нулю.
Не путать с общим уравнением квадратичной функции, графиком которого является парабола 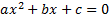
Пример выполнения задания
Задание 1. Указать коэффициенты А,В,С для каждого уравнения:
1) 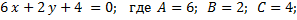
2) 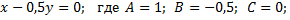
3) 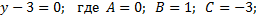
4) 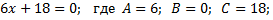
Уравнение прямой с угловым коэффициентом
Уравнение вида 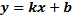 называется уравнением с угловым коэффициентом
называется уравнением с угловым коэффициентом 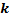 .
.
Данное уравнение можно получить после преобразования общего уравнения прямой.
Пример выполнения задания
Задание 2. Уравнения из задания 1 преобразовать в уравнения с угловым коэффициентом.
Указать наклон прямой по угловому коэффициенту.
Решение:
1) 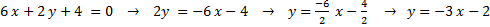
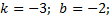 наклон прямой влево (в сторону отрицательных чисел);
наклон прямой влево (в сторону отрицательных чисел);
2) 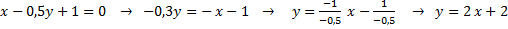
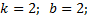 наклон прямой вправо (в сторону положительных чисел);
наклон прямой вправо (в сторону положительных чисел);
3) 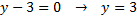
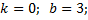 поэтому прямая параллельна оси О
поэтому прямая параллельна оси О 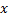
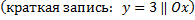 ;
;
4) 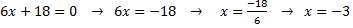
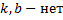 , поэтому прямая перпендикулярна оси
, поэтому прямая перпендикулярна оси 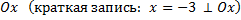 .
.
Угловой коэффициент может быть целым числом, десятичной, обычной или неправильной дробью. Причём, в последнем случае выделять целую часть дроби не нужно, так как уравнение в таком виде легче представить в общем виде.
Например, в уравнении 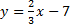 , где
, где 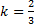
Умножив это уравнение на 3 получим общее уравнение прямой 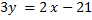 или
или 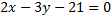
или в уравнении 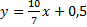 , где
, где 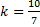
Умножив это уравнение на 7 получим общее уравнение прямой 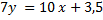 или
или 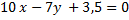
3) Уравнение прямой в отрезках на осях координат Если прямая задана графически и пересекает оси 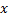 и и 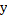 в точках с координатами в точках с координатами 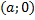 и и 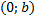 , то её уравнение имеет вид , то её уравнение имеет вид
Задание 3. Прямая пересекает оси координат в точках Преобразовать полученное уравнение в уравнения с угловым коэффициентом. Решение: Составляем уравнение в отрезках по формуле: Выполняем схематичный рисунок. Преобразуем уравнение, умножив его на 15:
Получили уравнение с угловым коэффициентом | 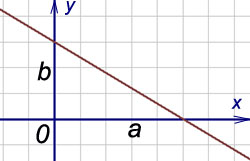 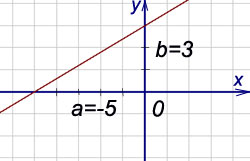 |
Уравнение прямой, проходящей через две точки
Если прямая проходит через две точки 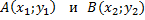 , такие что
, такие что 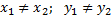 , то её уравнение
, то её уравнение
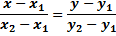 |
Пример выполнения задания
Задание 4. Записать уравнение прямой, проходящей через две точки 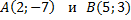 .
.
Преобразовать полученное уравнение в уравнения с угловым коэффициентом.
Запишем уравнение в отрезках по формуле:
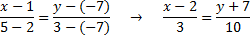
Преобразуем это уравнение в уравнение с угловым коэффициентом. Для этого получившуюся пропорцию запишем в строчку, перемножив числители и знаменатели крест-на крест:
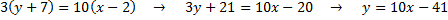
Получили уравнение с угловым коэффициентом 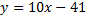 , где
, где 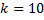
Каноническое уравнение прямой
Если известны координаты точки 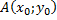 , лежащей на прямой, и известны координаты направляющего вектора
, лежащей на прямой, и известны координаты направляющего вектора 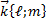 , то уравнение прямой имеет вид
, то уравнение прямой имеет вид
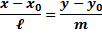
Пример выполнения задания
Задание 5. Записать уравнение прямой, заданной точкой 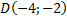 и направляющим вектором
и направляющим вектором 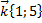 .
.
Преобразовать полученное уравнение в уравнения с угловым коэффициентом.
Решение:
Запишем каноническое уравнение прямой по формуле, где 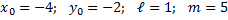 :
:
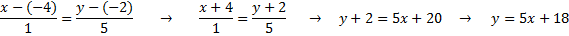
Получили уравнение с угловым коэффициентом 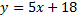 , где
, где 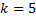
Контрольное задание №10 по теме
«Уравнение прямой на плоскости»
1) Записать общее уравнение прямой, имеющей следующие коэффициенты:
а) 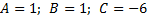 в)
в) 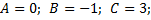
б) 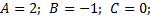 г)
г) 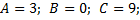
2) Получившиеся уравнения в задании 1 преобразовать в уравнения с угловым коэффициентом.
3) Прямая пересекает оси координат в точках 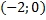 и
и 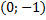 . Составить уравнение прямой в отрезках.
. Составить уравнение прямой в отрезках.
Выполнить схематичный рисунок, с указанием отсекаемых отрезков на осях координат.
Преобразовать полученное уравнение в уравнения с угловым коэффициентом.
4) Записать уравнение прямой, проходящей через две точки 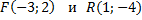
Преобразовать полученное уравнение в уравнения с угловым коэффициентом.
5) Записать уравнение прямой, заданной точкой 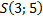 и направляющим вектором
и направляющим вектором 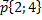 .
.
Преобразовать полученное уравнение в уравнения с угловым коэффициентом.

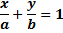
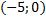 и
и 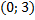 . Составить уравнение прямой в отрезках. Выполнить схематичный рисунок, с указанием отсекаемых отрезков на осях координат.
. Составить уравнение прямой в отрезках. Выполнить схематичный рисунок, с указанием отсекаемых отрезков на осях координат.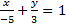
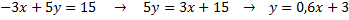
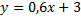 , где
, где 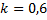 .
.