Основы теории вероятностей и математической статистики

Комбинаторика

Комбинаторика - раздел математики, в котором изучаются о подсчете числа комбинаций (выборок), получаемых из элементов заданного конечно­го множества. В каждой из них требуется ответить на вопрос «сколькими способами?».

Размещениями из 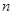элементов по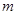 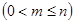элементов на­зываются соединения, каждое из которых состоит из 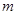элементов, взятых из данных 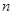элементов. При этом размещения отличаются друг от друга как самими элементами, так и их порядком.

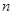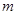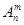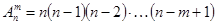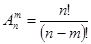Число размещений из элементов по элементов обозначается символом и вычисляется по формуле или , где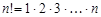

Перестановками из 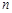элементов называются раз­мещения из элементов по элементов, отличающиеся друг от друга лишь порядком элементов. Число перестановок из 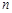эле­ментов обозначается символом 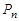и вычисляется по фор­муле: .

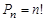Сочетаниями из 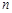элементов по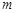 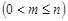элементов на­зываются соединения, каждое из которых состоит из элементов, взя­тых из данных 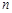элементов. Эти соединения отличаются друг от друга хотя бы одним элементом. В отличие от размещений, порядок следования элементов здесь не учитывается. Число сочетаний из 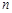элементов по 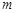элементов обозначается сим­волом 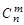и вычисляется по формуле: .

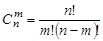Пример 1. Составить различные размещения по 2 из элементов мно­жества 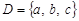; подсчитать их число.

Решение. Из трех элементов можно образовать следующие размещения по два элемента: 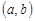, , 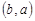, , 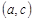, 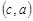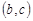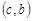. Согласно форму­ле (1) их число: 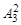= 3·2 = 6 .

Пример 2. Составить различные перестановки из элементов мно­жества 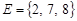; подсчитать их число.

Решение. Из элементов данного множества можно составить следующие пе­рестановки: (2,7,8); (2,8,7); (7,2,8); (7,8,2); (8,2,7); (8,7,2). По фор­муле (3) имеем: 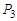= 3! = 1·2·3 = 6 .

Пример 3. Составить различные сочетания по 2 из элементов мно­жества 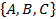; подсчитать их число.

Решение. Из трех элементов можно образовать следующие сочетания по два элемента: 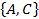; ; 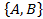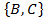. Их число: .

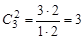Теория вероятностей

Предметтеории вероятностей - изучение вероятност­ных закономерностей, возникающих при рассмотрении массо­вых однотипных случайных событий.

Событие- это любое явление, в отношении которого имеет смысл говорить, наступило оно или не наступило, в ре­зультате определенного комплекса условий или случайного эксперимента. Обозначаются события заглавными латинскими буквами .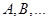

Примерами случайного эксперимента являются подбрасы­вание монеты, извлечение одной карты из перетасованной ко­лоды, подсчет числа автомобилей в очереди на бензоколонке в данный момент и т.д.

Вероятностью 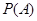события 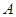называется отношение числа 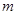– элементарных исходов испытания, благоприятствующих наступлению события A, к числу 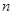– всех возможных элементарных исходов испытания.

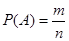
Пример 1. Найти вероятность, что при бросании монеты выпадет герб.

Решение. При бросании монеты имеются два равновозможных исхода: “выпадение герба” и “выпадение решки” 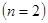. Для события 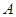– “выпадение герба” благоприятен только один из них 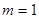. Значит, вероятность .

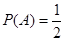Вероятность любого события заключена между нулем и единицей.

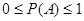
Можно выделить следующие виды случайных событий:

Событие называется достоверным,если оно обязательно происходит при каждом осуществлении определенной сово­купности условий. Например, если брошена игральная кость, то выпадение не менее одного и не более шести очков является достоверным событием. Вероятность достоверного события 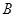равна единице: .

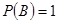Событие называется невозможным,если оно заведомо не произойдет ни при одном осуществлении данной совокупности условий. Например, если брошена игральная кость, то выпа­дение больше шести очков является невозможным событием. Вероятность невозможного события 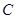равна нулю: .

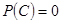Событие называется случайным,если оно может про­изойти, а может и не произойти при осуществлении данной совокупности условий. Например, если брошена игральная кость, то выпадение любого из шести очков является случай­ным событием. События называются несовместными, если их одновре­менное появление при осуществлении комплекса условий невозможно, т.е. появление события 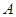в данном испытании исключает появление события 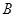в этом же испытании. На­пример, если из урны с черными и белыми шарами случайным образом извлекается шар ·черного цвета, то его появление ис­ключает извлечение белого шара в этой же попытке. События называются единственно возможными, если появление в результате испытания одного и только одного из них является достоверным событием. Например, если стрелок произвел выстрел по цели, то обязательно произойдет одно из двух событий - попадание или промах. Эти события единст­венно возможные. События называются равновозможными, если есть осно­вания считать, что ни одно из этих событий не является более возможным, чем другие. Например, появление герба и появ­ление надписи при бросании монеты есть события равновоз­можные, потому что предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндриче­скую форму, и наличие чеканки не влияет на выпадение той или иной стороны монеты. Если событие 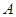- какое-либо событие, то событие, со­стоящее в том, что событие 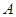не наступило, называется про­тивоположным событию и обозначается как 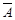.События, происходящие при реализации определенного комплекса условий или в результате случайного эксперимен­та, называются элементарными исходами. Считается, что при проведении случайного эксперимента реализуется только один из возможных элементарных исходов.