Теоремы сложения и умножения вероятностей
Суммой двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В.
Теорема сложения вероятностей
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
W (А + В) = W (А) + W(В).
Два события называются зависимыми, если вероятность одного из них зависит от наступления или не наступления другого. в случае зависимых событий вводится понятие условной вероятности события.
Условной вероятностью W(А/В) события А называется вероятность события А, вычисленная при условии, что событие В произошло. Аналогично через Р(В/А) обозначается условная вероятность события В при условии, что событие А наступило.
Произведением двух событий А и В называется событие С, состоящее в совместном появлении события А и события В.
Теорема умножения вероятностей
Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого:
W (АВ) = W(А) · W(В/А), или W (АВ) = W(В) · W(А/В).
Следствие. Вероятность совместного наступления двух независимых событий А и В равна произведению вероятностей этих событий:
W(АВ) = W(А) · W(В).
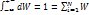 =1 – условие нормировки вероятности
=1 – условие нормировки вероятности
Распределение молекул по скоростям.
Найти распределение молекул по скоростям − это значит определить, сколько молекул
или, какая их часть из общего числа N имеют скорости, лежащие в интервале от v до v + dv.
Пусть ΔN − число молекул, обладающих скоростями в диапазоне значений от v до v + dv
Одинаковым для различных порций газа будет следующее отношение:
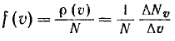
Определенная таким образом функция f(v) является функцией распределения. Зная вид этой функции можно найти число молекул ΔN.
Функция распределения была найдена теоретически Максвеллом и носит его имя.
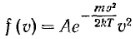 , где А – множитель, не зависящий от v, m – масса молекулы, k – постоянная Больцмана.
, где А – множитель, не зависящий от v, m – масса молекулы, k – постоянная Больцмана.
Т.к. 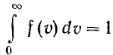 ,
,
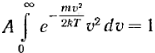 , откуда
, откуда
A = 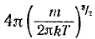
Таким образом, функция распределения Максвелла имеет вид:
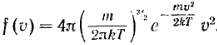
Распределение молекул по координатам
Определим закон изменения давления и плот-
ности земной атмосферы как функцию расстояния от её поверхности.
Применительно к слою газа толщиной
dh условие механического равновесия следует записать следующим образом:
(р+dp)s+ρgsdh-ps=0
Раскроем скобки: dp = -ρgdh
Ρ= m/V= pµ/RT
Подставим одно в другое: dp/p= - (µg/RT)*dh
Интегрируем: p(h)=p0*exp(-µgh/RT) – барометрическая формула.
Барометрическая формула по-
зволяет получить закон изменения с высотой количества молекул в единице объёма, для этого необходимо выразить давление через концентрацию молекул:
p=n*kв*t, n(h)=n0*exp(-µgh/RT)
