Для магнитного поля. Поле соленоида

По аналогии с электростатическим полем, введем такие важнейшие характеристики магнитного поля, как магнитный поток и циркуляция вектора .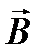

Магнитный поток сквозь произвольную поверхность S представляет собой число линий магнитной индукции, пронизывающих данную поверхность, и определяется выраже- нием
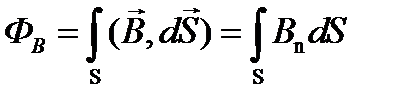, (1.20)
где 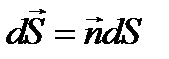, 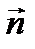- единичный вектор нормали к площадке dS, 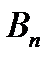- проекция вектора 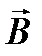на направление нормали.

В СИ магнитный поток измеряется в веберах(Вб):

.

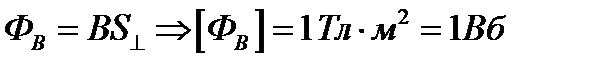В силу того, что линии индукции магнитного поля являют- ся замкнутыми, число линий , выходящих из любого объема, ограниченного замкнутой поверхностью, всегда равно числу линий, входящих в этот объем.

Следовательно, магнитный поток сквозь произвольную замкнутую поверхность равен нулю

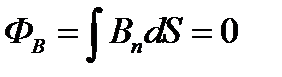. (1.21)

Данное выражение представляет собой теорему Гаусса для вектора .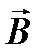

Перейдем теперь к определению циркуляции вектора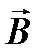

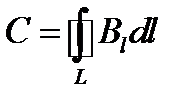, (1.22)
где 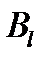- проекция вектора на направление 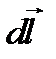, L - произволь- ный замкнутый контур.

Сначала вычислим циркуляцию вектора 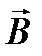по контуру,

охватывающему прямолинейный проводник с током (рис 1.6).

Рис.1.6

I2,,I4,,I5>0 I1,I3<0

α

dα I

dl

B

х

b)

I1

I2

I5

I4

I3

L

a)

b

Разобьем контур на элементы dl. В каждой точке контура вектор 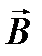направлен по касательной к окружности радиуса b с центром на оси проводника и численно равен

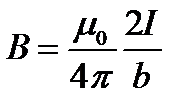. (1.23)

Произведя замену 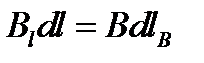, , 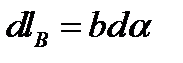получим

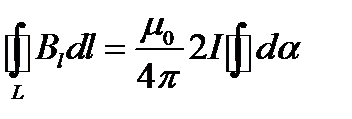. (1.24)

При обходе контура угол 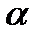изменяется от 0 до 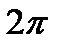, поэтому

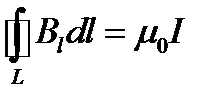. (1.25)

Если ток создается системой произвольных проводников с токами 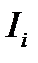, то в соответствии с принципом суперпозиции, получим

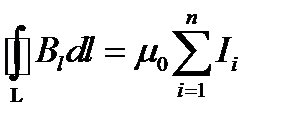. (1.26)

Таким образом, циркуляция вектора магнитной индук- ции поля в вакууме вдоль произвольного замкнутого контура равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых контуром.

Ток считается положительным, если его направление связано с направлением обхода контура правилом правого винта, ток противоположного направления – отрицательным.

Тот факт, что циркуляция вектора не равна нулю, означает, что магнитное поле не потенциально. Ему нельзя приписать скалярный потенциал, поскольку он был бы неоднозначным. Такое поле называют вихревым или соленоидальным.

Теорема о циркуляции вектора играет в магнито-статике ту же роль, что и теорема Гаусса в электростатике. При наличии определенной симметрии в распределении токов теорема о циркуляции оказывается весьма эффектив- ной для расчета индукции магнитного поля. Покажем это на примере расчета магнитного поля соленоида.

Соленоидпредставляет собой цилиндрическую катушку, длина которой значительно больше ее диаметра. Поле внутри соленоида является однородным, а вне соленоида – неоднородным и очень слабым. Чем длиннее соленоид, тем меньше значение магнитной индукции вне соленоида. Для бесконечно длинного соленоида магнитное поле снаружи отсутствует вообще.

Найдем магнитную индукцию внутри длинного соленоида, на единицу длины которого приходится n витков проводника, и по которому течет ток I. С этой целью рассмотрим прямоугольный замкнутый контур, одна из сторон которого параллельна оси соленоида и равняется l (рис.1.7). Циркуляцию вектора по данному контору можно предста- вить следующим образом:

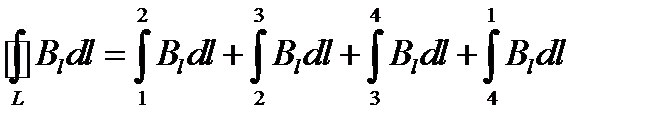
Рис.2.7

. .
Так как поле вне соленоида практически отсутствует и вектор перпендикулярен к участкам 2-3 и 4-1, то все слагаемые, кроме первого равны нулю. Поэтому,

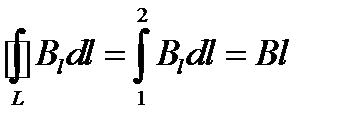. (1.27)

С другой стороны, по теореме о циркуляции можно написать 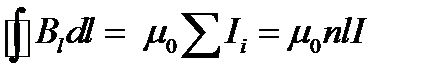, (1.28)

В=0

Рис.1.7

где n – плотность намотки (число витков на единице длины соленоида).

Из формул (1.27) и (1.28) следует

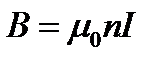. (1.29)

Полученная формула и определяет магнитное поле соленоида в вакууме.

.