И метода определения инерции тела

Исследуемое тело 1 пред­став­ляет собой металлическую пластину с двумя вырезами (рис. 3.2). Этими вырезами тело подвешивается на опору - кронштейн 2 для организации колебаний. Чтобы уменьшить трение и износ детали точки подвеса О₁ и О₂ снабжены специальными подставками 3. На конце кронштейна может быть подвешен математический маятник 4, длину которого можно изменять.

В работе определяются моменты инерции I₁ и I₂относительно осей О₁ и О₂. Метод определения моментов инерции основан на том, что период колебаний ФМ (пластина в данном случае играет роль физического маятника) связан с его моментом инерции относительно оси колебания (см. формулу (3.8)). Таким образом, измерив на опыте период колебаний маятника Т и расстояние b от точки подвеса до центра масс (см. рис.3.1), зная массу m маятника и ускорение свободного падения g, можно вычислить момент инерции:

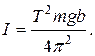(3.12)

Порядок выполнения работы

1. Снять пластину с подвеса, измерить линейкой расстояния b₁ = O₁C и b₂ = O₂C (см. рис. 3.2) и оценить ошибку Db этих измерений. Результаты занести в табл.1; сюда же вписать данные о массе тела и ускорении свободного падения.

2. Подвесить маятник на ось О₁, привести его в движение (j £ 8^о) и измерить время t₁ для 30-50 полных колебаний (N). (Отсчет времени лучше начинать после того, как тело совершит несколько колебаний). Опыт повторить не менее 5 раз при одном и том же числе колебаний. Результаты (эти и последующие) занести в табл.1.

3. Снять маятник и, подвесив его на ось О₂, проделать то же, что и в п.2.

4. Вычислить Т₁ и Т₂ для каждого из опытов и их средние значения <T₁> и <T₂>.

Таблица 1

№№	Число полн.	Колебания а оси О1	Колебания на оси О2
n/n	колеб. N	t1	Т1,i	t2	T2,i	(T2i - <T2>)	(T2i - <T2>)2
. .
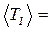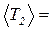Другие b1 = ± m = ± L1 = данные b2 = ± g = ± L2 =

5. По формуле

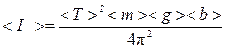
(см. (3.12)) вычислить <I₁> и <I₂>.

6. Для момента инерции I₂ вычислить относительную e_I2 и абсолютную DI₂ погрешности (для I₁ первую из них принять такой же).

Для этого:

а) подсчитать Т_2i - <Т₂>, (T_2i - <T₂>)², 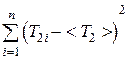(cм. табл. 1);

б) вычислить абсолютную погрешность в измерении периода

колебаний

,

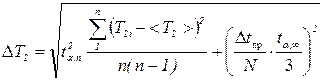где n - число измерений; Dt_пр - приборная погрешность секундомера; t_{a,n -} коэффициент Стьюдента (определяется по таблице в зависимости от выбранной надежности a и n); N – число полных колебаний.

в) определить относительную погрешность;

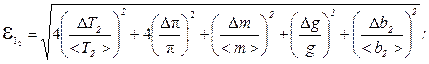
г) вычислить абсолютную погрешность в определении I₂:

DI₂ = e_I<I₂>;

7. Результаты представить в виде:

I₁ = <I₁> ± DI₁

I₂ = <I₂> ± DI₂

приa = , e_I = % .

8. Вычислить приведенные длины L₁ и L₂ маятников по формуле

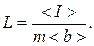
9. При наличии математического маятника установить его длину l равной L₁ (или L₂) и убедиться в синхронности колебаний физического и математического маятников.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Физический маятник.

2. Уравнения колебаний физического маятника (дифференциальное уравнение и его решение).

3. Частота и период колебаний физического маятника.

4. Приведенная длина физического маятника.

5. Точка подвеса и центр качаний физического маятника.

6. Метод определения I в данной работе.

7. Порядок выполнения работы.

ЛАБОРАТОРНАЯ РАБОТА № 4

ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ

Цель работы:ознакомиться с методом моделирования электростатического поля с помощью электропроводной бумаги; исследовать электростатическое поле плоского и цилиндрического конденсаторов.

Приборы и принадлежности: источник постоянного тока, вольтметр, электропроводная бумага, планшет с набором электродов, проводники, один из которых снабжен зондом.

Сведения из теории

Электростатическое поле (ЭСП)- форма материи, осуществляющая взаимодействие между заряженными телами.

Основным свойствомполя является его силовое действиена любой заряд, помещенный в поле.

Источником ЭСП является неподвижный заряд (заряженное тело).

Количественными характеристиками ЭСП являются напряженность и потенциал.

Напряженность поля - векторная физическая величина, характеризующая силовое действие поля в точке, численно равная силе, с которой поле действовало бы на положительный единичный заряд, помещенный в данную точку поля и по направлению совпадающая с направлением действия этой силы.

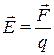, (4.1)

здесь 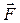- сила, действующая на заряд + q, помещенный в данную точку поля.

Таким образом, напряженность - это силовая характеристика поля. Единица напряженности - Н/Кл (В/м). Если напряженность поля во всех точках одинаковапо величине и направлению, то поле называют однородным, в противном случае - неоднородным.

Потенциал поля в точке -это скалярная физическая величина, характеризующая энергетические свойства поля, численно равная потенциальной энергии положительного единичного заряда, помещенного в данную точку поля.

, (4.2)

здесь W_п- потенциальная энергия заряда +q, помещенного в некоторую точку поля. Единицей потенциала является В (Дж/Кл). Потенциал - энергетическая характеристика поля.

Потенциальная энергия, а вместе с ней и потенциал задаются с точностью до постоянной. Чтобы потенциал приобрел вполне определенное значение, надо придать ему некоторое значение в одной из точек поля. В физике принято считать j = 0 в точке, удаленной бесконечно далеко от заряженного тела.

Надо, однако, помнить, что хотя для любой точки поля можно указать такую величину, как потенциал, ясный физический смысл имеет только разность потенциалов двух точек поля (j₁ - j₂): она равна работе поля по перемещению единицы положительного заряда из одной точки (1) в другую (2). Измерить практически можно тоже только разность потенциалов. И, говоря об измерении потенциала, подразумевают измерение разности потенциалов двух точек, потенциал одной из которых условно принимается за нуль.

Из определения разности потенциалов двух точек поля следует, что работа поля по перемещению заряда +q из точки 1 в точку 2 может быть вычислена по формуле

А = q (j₁ - j₂).(4.3)

Электростатическое поле можно изобразить графически. Делается это с помощью линий напряженности (силовых линий) и эквипотенциальных поверхностей.

Линией напряженности называется линия, касательная к которой в каждой точке совпадает с направлением напряженности поля в этой точке (рис. 4.1 - сплошные кривые).

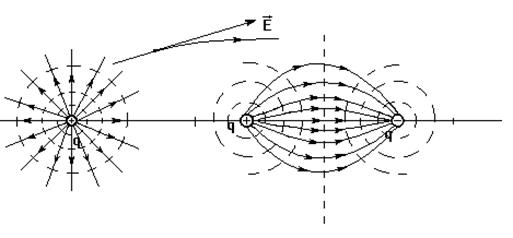Рис. 4.1

Эквипотенциальная поверхность - поверхность равного потенциала (на рис. 4.1 пунктирные линии - линии пересечения этих поверхностей с плоскостью рисунка).

Так как работа поля по перемещению заряда вдоль эквипотенциальной поверхности равна нулю (j₁ = j₂), то это значит, что линии напряженности в любой точке поля перпендикулярны эквипотенциальным поверхностям.

Напряженность и разность потенциалов поля связаны между собой. В общем случае эта связь выглядит так:

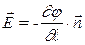или 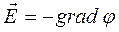. (4.4)

Здесь производная по расстоянию берется вдоль линии напряженности в направлении, совпадающем с направлением единичного вектора нормалиn к эквипотенциальной поверхности. Из уравнений (4.4) видно, что векторE всегда направлен в сторону уменьшения потенциала.

В случае однородного поля модуль вектора напряженности связан с разностью потенциалов соотношением:

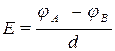, (4.5)

где j_А и j _В - потенциалы двух точек (А и В), лежащих на одной линии напряженности, а d - расстояние между этими точками.

Таким образом, зная закон изменения потенциала вдоль силовой линии, можно в любой точке поля определить напряженность поля, численное значение которой равно изменению потенциала на единице длины силовой линии. Отсюда следует еще одна единица измерения напряженности - B/м.